add README.md of cgmres

nmpc/cgmres/README.md

@@ -0,0 +1,79 @@
+# CGMRES method of Nonlinear Model Predictive Control
+This program is about Continuous gmres method for NMPC
+Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
+By using CGMRES, we can pass the calculating step and get the optimal input quickly.
+
+# Problem Formulation
+
+- **example**
+
+- model
+
+<a href="https://www.codecogs.com/eqnedit.php?latex=\begin{bmatrix}&space;\dot{x_1}&space;\\&space;\dot{x_2}&space;\\&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;x_2&space;\\&space;(1-x_1^2-x_2^2)x_2-x_1&plus;u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\begin{bmatrix}&space;\dot{x_1}&space;\\&space;\dot{x_2}&space;\\&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;x_2&space;\\&space;(1-x_1^2-x_2^2)x_2-x_1&plus;u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5" title="\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \\ \end{bmatrix} = \begin{bmatrix} x_2 \\ (1-x_1^2-x_2^2)x_2-x_1+u \\ \end{bmatrix}, |u| \leq 0.5" /></a>
+
+- evaluation function
+
+<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\frac{1}{2}(x_1^2(t&plus;T)&plus;x_2^2(t&plus;T))&plus;\int_{t}^{t&plus;T}\frac{1}{2}(x_1^2&plus;x_2^2&plus;u^2)-0.01vd\tau" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\frac{1}{2}(x_1^2(t&plus;T)&plus;x_2^2(t&plus;T))&plus;\int_{t}^{t&plus;T}\frac{1}{2}(x_1^2&plus;x_2^2&plus;u^2)-0.01vd\tau" title="J = \frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" /></a>
+
+
+- **two wheeled model**
+
+- model
+
+<a href="https://www.codecogs.com/eqnedit.php?latex=\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" title="\frac{d}{dt} \boldsymbol{X}= \frac{d}{dt} \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} u_v \\ u_\omega \\ \end{bmatrix} = \boldsymbol{B}\boldsymbol{U}" /></a>
+
+- evaluation function
+
+<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\boldsymbol{X}(t_0&plus;T)^2&space;&plus;&space;\int_{t_0}^{t_0&space;&plus;&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\boldsymbol{X}(t_0&plus;T)^2&space;&plus;&space;\int_{t_0}^{t_0&space;&plus;&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" title="J = \boldsymbol{X}(t_0+T)^2 + \int_{t_0}^{t_0 + T} \boldsymbol{U}(t)^2 - 0.01 dummy_{u_v} - dummy_{u_\omega} dt" /></a>
+
+
+if you want to see more detail about this methods, you should go https://qiita.com/MENDY/items/4108190a579395053924.
+However, it is written in Japanese
+
+# Expected Results
+
+- example
+
+![Figure_1.png](https://qiita-image-store.s3.amazonaws.com/0/261584/3347fb3c-3fce-63fe-36d5-8a7bb053531a.png)
+
+- two wheeled model
+
+- trajectory
+
+![image.png](https://qiita-image-store.s3.amazonaws.com/0/261584/8e39150d-24ed-af13-51f0-0ca97cb5f5ec.png)
+
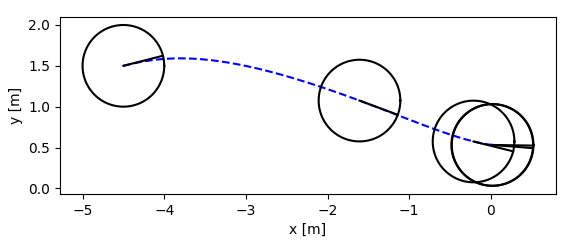
+- time history
+
+![Figure_1.png](https://qiita-image-store.s3.amazonaws.com/0/261584/e67794f3-e8ef-5162-ea84-eb6adefd4241.png)
+![Figure_2.png](https://qiita-image-store.s3.amazonaws.com/0/261584/d74fa06d-2eae-5aea-4a33-6c63e284341e.png)
+
+# Usage
+
+- for example
+
+```
+$ python main_example.py
+```
+
+- for two wheeled
+
+```
+$ python main_two_wheeled.py
+```
+
+# Requirement
+
+- python3.5 or more
+- numpy
+- matplotlib
+
+# Reference
+I`m sorry that main references are written in Japanese
+
+- main (commentary article) (Japanse)　https://qiita.com/MENDY/items/4108190a579395053924
+
+- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
+
+- 非線形最適制御入門（コロナ社）
+
+- 実時間最適化による制御の実応用（コロナ社）