add newton method
This commit is contained in:
parent
17250480d7
commit
aa323cdf1d
|
|
@ -8,6 +8,7 @@ Now you can see the examples of control theories as following
|
|||
|
||||
- **Iterative Linear Quadratic Regulator (iLQR)**
|
||||
- **Nonlinear Model Predictive Control (NMPC) with CGMRES**
|
||||
- **Nonlinear Model Predictive Control (NMPC) with Newton method**
|
||||
- **Linear Model Predictive Control (MPC)**(as generic function such as matlab tool box)
|
||||
- **Extended Linear Model Predictive Control for vehicle model**
|
||||
|
||||
|
|
|
|||
|
|
@ -1,7 +1,8 @@
|
|||
# CGMRES method of Nonlinear Model Predictive Control
|
||||
This program is about Continuous gmres method for NMPC
|
||||
Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
|
||||
By using CGMRES, we can pass the calculating step and get the optimal input quickly.
|
||||
# Newton method of Nonlinear Model Predictive Control
|
||||
This program is about NMPC with newton method.
|
||||
Usually we have to calculate the partial differential of optimal matrix.
|
||||
In this program, in stead of using any paticular methods to calculate the partial differential of optimal matrix, I used numerical differentiation.
|
||||
Therefore, I believe that it easy to understand and extend your model.
|
||||
|
||||
# Problem Formulation
|
||||
|
||||
|
|
@ -13,39 +14,26 @@ By using CGMRES, we can pass the calculating step and get the optimal input quic
|
|||
|
||||
- evaluation function
|
||||
|
||||
To consider the constraints of input u, I introduced dummy input.
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" title="J = \frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" /></a>
|
||||
|
||||
|
||||
- **two wheeled model**
|
||||
|
||||
- model
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" title="\frac{d}{dt} \boldsymbol{X}= \frac{d}{dt} \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} u_v \\ u_\omega \\ \end{bmatrix} = \boldsymbol{B}\boldsymbol{U}" /></a>
|
||||
|
||||
- evaluation function
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\boldsymbol{X}(t_0+T)^2&space;+&space;\int_{t_0}^{t_0&space;+&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\boldsymbol{X}(t_0+T)^2&space;+&space;\int_{t_0}^{t_0&space;+&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" title="J = \boldsymbol{X}(t_0+T)^2 + \int_{t_0}^{t_0 + T} \boldsymbol{U}(t)^2 - 0.01 dummy_{u_v} - dummy_{u_\omega} dt" /></a>
|
||||
|
||||
|
||||
if you want to see more detail about this methods, you should go https://qiita.com/MENDY/items/4108190a579395053924.
|
||||
However, it is written in Japanese
|
||||
coming soon !
|
||||
|
||||
# Expected Results
|
||||
|
||||
- example
|
||||
|
||||

|
||||
![Figure_1.png]()
|
||||
|
||||
you can confirm that the my method could consider the constraints of input.
|
||||
|
||||
- two wheeled model
|
||||
|
||||
- trajectory
|
||||
|
||||
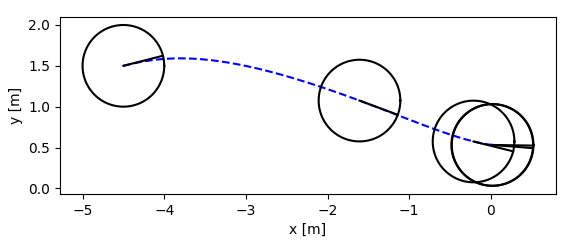
|
||||
|
||||
- time history
|
||||
|
||||

|
||||

|
||||
coming soon !
|
||||
|
||||
# Usage
|
||||
|
||||
|
|
@ -57,9 +45,7 @@ $ python main_example.py
|
|||
|
||||
- for two wheeled
|
||||
|
||||
```
|
||||
$ python main_two_wheeled.py
|
||||
```
|
||||
coming soon !
|
||||
|
||||
# Requirement
|
||||
|
||||
|
|
|
|||
|
|
@ -407,19 +407,13 @@ class NMPCControllerWithNewton():
|
|||
"""
|
||||
Attributes
|
||||
------------
|
||||
zeta : float
|
||||
gain of optimal answer stability
|
||||
tf : float
|
||||
predict time
|
||||
alpha : float
|
||||
gain of predict time
|
||||
N : int
|
||||
predicte step, discritize value
|
||||
threshold : float
|
||||
cgmres's threshold value
|
||||
input_num : int
|
||||
newton's threshold value
|
||||
NUM_INPUT : int
|
||||
system input length, this should include dummy u and constraint variables
|
||||
max_iteration : int
|
||||
MAX_ITERATION : int
|
||||
decide by the solved matrix size
|
||||
simulator : NMPCSimulatorSystem class
|
||||
us : list of float
|
||||
|
|
@ -444,11 +438,10 @@ class NMPCControllerWithNewton():
|
|||
None
|
||||
"""
|
||||
# parameters
|
||||
self.tf = 1. # 最終時間
|
||||
self.N = 10 # 分割数
|
||||
self.threshold = 0.0001 # break値
|
||||
self.N = 10 # time step
|
||||
self.threshold = 0.0001 # break
|
||||
|
||||
self.NUM_INPUT = 3 # dummy, 制約条件に対するrawにも合わせた入力の数
|
||||
self.NUM_INPUT = 3 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
|
||||
self.Jacobian_size = self.NUM_INPUT * self.N
|
||||
|
||||
# newton parameters
|
||||
|
|
@ -492,11 +485,6 @@ class NMPCControllerWithNewton():
|
|||
|
||||
# Newton method
|
||||
for i in range(self.MAX_ITERATION):
|
||||
# check
|
||||
# print("all_us = {}".format(all_us))
|
||||
# print("newton iteration in {}".format(i))
|
||||
# input()
|
||||
|
||||
# calc all state
|
||||
x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
|
||||
|
||||
|
|
@ -504,8 +492,6 @@ class NMPCControllerWithNewton():
|
|||
F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
|
||||
|
||||
# judge
|
||||
# print("F_hat = {}".format(F_hat))
|
||||
# print(np.linalg.norm(F_hat))
|
||||
if np.linalg.norm(F_hat) < self.threshold:
|
||||
# print("break!!")
|
||||
break
|
||||
|
|
@ -531,9 +517,6 @@ class NMPCControllerWithNewton():
|
|||
|
||||
F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
|
||||
|
||||
# print("check val of F = {0}".format(np.linalg.norm(F)))
|
||||
# input()
|
||||
|
||||
# for save
|
||||
self.history_f.append(np.linalg.norm(F))
|
||||
self.history_u.append(self.us[0])
|
||||
|
|
@ -641,7 +624,4 @@ def main():
|
|||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
|
||||
main()
|
||||
Loading…
Reference in New Issue