diff --git a/.gitignore b/.gitignore
index 1c52168..b467fc0 100644
--- a/.gitignore
+++ b/.gitignore
@@ -1,10 +1,134 @@
-*.csv
-*.log
-*.pickle
-*.mp4
+# folders
+.vscode/
+.pytest_cache/
+result/
-.cache/
-.eggs/
+# Byte-compiled / optimized / DLL files
__pycache__/
-.pytest_cache
-cache/
\ No newline at end of file
+*.py[cod]
+*$py.class
+
+# C extensions
+*.so
+
+# Distribution / packaging
+.Python
+build/
+develop-eggs/
+dist/
+downloads/
+eggs/
+.eggs/
+lib/
+lib64/
+parts/
+sdist/
+var/
+wheels/
+pip-wheel-metadata/
+share/python-wheels/
+*.egg-info/
+.installed.cfg
+*.egg
+MANIFEST
+
+# PyInstaller
+# Usually these files are written by a python script from a template
+# before PyInstaller builds the exe, so as to inject date/other infos into it.
+*.manifest
+*.spec
+
+# Installer logs
+pip-log.txt
+pip-delete-this-directory.txt
+
+# Unit test / coverage reports
+htmlcov/
+.tox/
+.nox/
+.coverage
+.coverage.*
+.cache
+nosetests.xml
+coverage.xml
+*.cover
+*.py,cover
+.hypothesis/
+.pytest_cache/
+
+# Translations
+*.mo
+*.pot
+
+# Django stuff:
+*.log
+local_settings.py
+db.sqlite3
+db.sqlite3-journal
+
+# Flask stuff:
+instance/
+.webassets-cache
+
+# Scrapy stuff:
+.scrapy
+
+# Sphinx documentation
+docs/_build/
+
+# PyBuilder
+target/
+
+# Jupyter Notebook
+.ipynb_checkpoints
+
+# IPython
+profile_default/
+ipython_config.py
+
+# pyenv
+.python-version
+
+# pipenv
+# According to pypa/pipenv#598, it is recommended to include Pipfile.lock in version control.
+# However, in case of collaboration, if having platform-specific dependencies or dependencies
+# having no cross-platform support, pipenv may install dependencies that don't work, or not
+# install all needed dependencies.
+#Pipfile.lock
+
+# PEP 582; used by e.g. github.com/David-OConnor/pyflow
+__pypackages__/
+
+# Celery stuff
+celerybeat-schedule
+celerybeat.pid
+
+# SageMath parsed files
+*.sage.py
+
+# Environments
+.env
+.venv
+env/
+venv/
+ENV/
+env.bak/
+venv.bak/
+
+# Spyder project settings
+.spyderproject
+.spyproject
+
+# Rope project settings
+.ropeproject
+
+# mkdocs documentation
+/site
+
+# mypy
+.mypy_cache/
+.dmypy.json
+dmypy.json
+
+# Pyre type checker
+.pyre/
diff --git a/LICENSE b/LICENSE
old mode 100755
new mode 100644
index 9a5e36b..0340be2
--- a/LICENSE
+++ b/LICENSE
@@ -1,6 +1,6 @@
MIT License
-Copyright (c) 2018 Shunichi Sekiguchi
+Copyright (c) 2020 Shunichi Sekiguchi
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
diff --git a/PythonLinearNonlinearControl/__init__.py b/PythonLinearNonlinearControl/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/common/__init__.py b/PythonLinearNonlinearControl/common/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/common/utils.py b/PythonLinearNonlinearControl/common/utils.py
new file mode 100644
index 0000000..07ff604
--- /dev/null
+++ b/PythonLinearNonlinearControl/common/utils.py
@@ -0,0 +1,2 @@
+import numpy as np
+
diff --git a/PythonLinearNonlinearControl/configs/__init__.py b/PythonLinearNonlinearControl/configs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/configs/first_order_lag.py b/PythonLinearNonlinearControl/configs/first_order_lag.py
new file mode 100644
index 0000000..18f86c9
--- /dev/null
+++ b/PythonLinearNonlinearControl/configs/first_order_lag.py
@@ -0,0 +1,92 @@
+import numpy as np
+
+class FirstOrderLagConfigModule():
+ # parameters
+ ENV_NAME = "FirstOrderLag-v0"
+ TYPE = "Linear"
+ TASK_HORIZON = 1000
+ PRED_LEN = 10
+ STATE_SIZE = 4
+ INPUT_SIZE = 2
+ DT = 0.05
+ # cost parameters
+ R = np.eye(INPUT_SIZE)
+ Q = np.eye(STATE_SIZE)
+ Sf = np.eye(STATE_SIZE)
+ # bounds
+ INPUT_LOWER_BOUND = np.array([-0.5, -0.5])
+ INPUT_UPPER_BOUND = np.array([0.5, 0.5])
+ # DT_INPUT_LOWER_BOUND = np.array([-0.5 * DT, -0.5 * DT])
+ # DT_INPUT_UPPER_BOUND = np.array([0.25 * DT, 0.25 * DT])
+ DT_INPUT_LOWER_BOUND = None
+ DT_INPUT_UPPER_BOUND = None
+
+ def __init__(self):
+ """
+ Args:
+ save_dit (str): save directory
+ """
+ # opt configs
+ self.opt_config = {
+ "Random": {
+ "popsize": 5000
+ },
+ "CEM": {
+ "popsize": 500,
+ "num_elites": 50,
+ "max_iters": 15,
+ "alpha": 0.3,
+ "init_var":1.,
+ "threshold":0.001
+ },
+ "MPPI":{
+ "beta" : 0.6,
+ "popsize": 5000,
+ "kappa": 0.9,
+ "noise_sigma": 0.5,
+ },
+ "iLQR":{
+ },
+ "cgmres-NMPC":{
+ },
+ "newton-NMPC":{
+ },
+ }
+
+ @staticmethod
+ def input_cost_fn(u):
+ """ input cost functions
+ Args:
+ u (numpy.ndarray): input, shape(input_size, )
+ or shape(pop_size, input_size)
+ Returns:
+ cost (numpy.ndarray): cost of input, none or shape(pop_size, )
+ """
+ return (u**2) * np.diag(FirstOrderLagConfigModule.R)
+
+ @staticmethod
+ def state_cost_fn(x, g_x):
+ """ state cost function
+ Args:
+ x (numpy.ndarray): state, shape(pred_len, state_size)
+ or shape(pop_size, pred_len, state_size)
+ g_x (numpy.ndarray): goal state, shape(state_size, )
+ or shape(pop_size, state_size)
+ Returns:
+ cost (numpy.ndarray): cost of state, none or shape(pop_size, )
+ """
+ return ((x - g_x)**2) * np.diag(FirstOrderLagConfigModule.Q)
+
+ @staticmethod
+ def terminal_state_cost_fn(terminal_x, terminal_g_x):
+ """
+ Args:
+ terminal_x (numpy.ndarray): terminal state,
+ shape(state_size, ) or shape(pop_size, state_size)
+ terminal_g_x (numpy.ndarray): terminal goal state,
+ shape(state_size, ) or shape(pop_size, state_size)
+ Returns:
+ cost (numpy.ndarray): cost of state, none or shape(pop_size, )
+ """
+ return ((terminal_x - terminal_g_x)**2) \
+ * np.diag(FirstOrderLagConfigModule.Sf)
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/configs/make_configs.py b/PythonLinearNonlinearControl/configs/make_configs.py
new file mode 100644
index 0000000..fb54981
--- /dev/null
+++ b/PythonLinearNonlinearControl/configs/make_configs.py
@@ -0,0 +1,9 @@
+from .first_order_lag import FirstOrderLagConfigModule
+
+def make_config(args):
+ """
+ Returns:
+ config (ConfigModule class): configuration for the each env
+ """
+ if args.env == "FirstOrderLag":
+ return FirstOrderLagConfigModule()
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/__init__.py b/PythonLinearNonlinearControl/controllers/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/controllers/cem.py b/PythonLinearNonlinearControl/controllers/cem.py
new file mode 100644
index 0000000..238ff39
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/cem.py
@@ -0,0 +1,135 @@
+from logging import getLogger
+
+import numpy as np
+import scipy.stats as stats
+
+from .controller import Controller
+from ..envs.cost import calc_cost
+
+logger = getLogger(__name__)
+
+class CEM(Controller):
+ """ Cross Entropy Method for linear and nonlinear method
+
+ Attributes:
+ history_u (list[numpy.ndarray]): time history of optimal input
+ Ref:
+ Chua, K., Calandra, R., McAllister, R., & Levine, S. (2018).
+ Deep reinforcement learning in a handful of trials
+ using probabilistic dynamics models.
+ In Advances in Neural Information Processing Systems (pp. 4754-4765).
+ """
+ def __init__(self, config, model):
+ super(CEM, self).__init__(config, model)
+
+ # model
+ self.model = model
+
+ # general parameters
+ self.pred_len = config.PRED_LEN
+ self.input_size = config.INPUT_SIZE
+
+ # cem parameters
+ self.alpha = config.opt_config["CEM"]["alpha"]
+ self.pop_size = config.opt_config["CEM"]["popsize"]
+ self.max_iters = config.opt_config["CEM"]["max_iters"]
+ self.num_elites = config.opt_config["CEM"]["num_elites"]
+ self.epsilon = config.opt_config["CEM"]["threshold"]
+ self.init_var = config.opt_config["CEM"]["init_var"]
+ self.opt_dim = self.input_size * self.pred_len
+
+ # get bound
+ self.input_upper_bounds = np.tile(config.INPUT_UPPER_BOUND,
+ self.pred_len)
+ self.input_lower_bounds = np.tile(config.INPUT_LOWER_BOUND,
+ self.pred_len)
+
+ # get cost func
+ self.state_cost_fn = config.state_cost_fn
+ self.terminal_state_cost_fn = config.terminal_state_cost_fn
+ self.input_cost_fn = config.input_cost_fn
+
+ # init mean
+ self.init_mean = np.tile((config.INPUT_UPPER_BOUND \
+ + config.INPUT_LOWER_BOUND) / 2.,
+ self.pred_len)
+ self.prev_sol = self.init_mean.copy()
+ # init variance
+ var = np.ones_like(config.INPUT_UPPER_BOUND) \
+ * config.opt_config["CEM"]["init_var"]
+ self.init_var = np.tile(var, self.pred_len)
+
+ # save
+ self.history_u = []
+
+ def clear_sol(self):
+ """ clear prev sol
+ """
+ logger.debug("Clear Sol")
+ self.prev_sol = self.init_mean.copy()
+
+ def obtain_sol(self, curr_x, g_xs):
+ """ calculate the optimal inputs
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ g_xs (numpy.ndarrya): goal trajectory, shape(plan_len, state_size)
+ Returns:
+ opt_input (numpy.ndarray): optimal input, shape(input_size, )
+ """
+ # initialize
+ opt_count = 0
+
+ # get configuration
+ mean = self.prev_sol.flatten().copy()
+ var = self.init_var.flatten().copy()
+
+ # make distribution
+ X = stats.truncnorm(-1, 1,
+ loc=np.zeros_like(mean),\
+ scale=np.ones_like(mean))
+
+ while (opt_count < self.max_iters) and np.max(var) > self.epsilon:
+ # constrained
+ lb_dist = mean - self.input_lower_bounds
+ ub_dist = self.input_upper_bounds - mean
+ constrained_var = np.minimum(np.minimum(np.square(lb_dist),
+ np.square(ub_dist)),
+ var)
+
+ # sample
+ samples = X.rvs(size=[self.pop_size, self.opt_dim]) \
+ * np.sqrt(constrained_var) \
+ + mean
+
+ # calc cost
+ # samples.shape = (pop_size, opt_dim)
+ costs = self.calc_cost(curr_x,
+ samples.reshape(self.pop_size,
+ self.pred_len,
+ self.input_size),
+ g_xs)
+
+ # sort cost
+ elites = samples[np.argsort(costs)][:self.num_elites]
+
+ # new mean
+ new_mean = np.mean(elites, axis=0)
+ new_var = np.var(elites, axis=0)
+
+ # soft update
+ mean = self.alpha * mean + (1. - self.alpha) * new_mean
+ var = self.alpha * var + (1. - self.alpha) * new_var
+
+ logger.debug("Var = {}".format(np.max(var)))
+ logger.debug("Costs = {}".format(np.mean(costs)))
+ opt_count += 1
+
+ sol = mean.copy()
+ self.prev_sol = np.concatenate((mean[self.input_size:],
+ np.zeros(self.input_size)))
+
+ return sol.reshape(self.pred_len, self.input_size).copy()[0]
+
+ def __str__(self):
+ return "CEM"
diff --git a/PythonLinearNonlinearControl/controllers/controller.py b/PythonLinearNonlinearControl/controllers/controller.py
new file mode 100644
index 0000000..4e63be5
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/controller.py
@@ -0,0 +1,66 @@
+import numpy as np
+
+from ..envs.cost import calc_cost
+
+class Controller():
+ """ Controller class
+ """
+ def __init__(self, config, model):
+ """
+ """
+ self.config = config
+ self.model = model
+
+ # get cost func
+ self.state_cost_fn = config.state_cost_fn
+ self.terminal_state_cost_fn = config.terminal_state_cost_fn
+ self.input_cost_fn = config.input_cost_fn
+
+ def obtain_sol(self, curr_x, g_xs):
+ """ calculate the optimal inputs
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ g_xs (numpy.ndarrya): goal trajectory, shape(plan_len, state_size)
+ Returns:
+ opt_input (numpy.ndarray): optimal input, shape(input_size, )
+ """
+ raise NotImplementedError("Implement gradient of hamitonian with respect to the state")
+
+ def calc_cost(self, curr_x, samples, g_xs):
+ """ calculate the cost of input samples
+
+ Args:
+ curr_x (numpy.ndarray): shape(state_size),
+ current robot position
+ samples (numpy.ndarray): shape(pop_size, opt_dim),
+ input samples
+ g_xs (numpy.ndarray): shape(pred_len, state_size),
+ goal states
+ Returns:
+ costs (numpy.ndarray): shape(pop_size, )
+ """
+ # get size
+ pop_size = samples.shape[0]
+ g_xs = np.tile(g_xs, (pop_size, 1, 1))
+
+ # calc cost, pred_xs.shape = (pop_size, pred_len+1, state_size)
+ pred_xs = self.model.predict_traj(curr_x, samples)
+
+ # get particle cost
+ costs = calc_cost(pred_xs, samples, g_xs,
+ self.state_cost_fn, self.input_cost_fn, \
+ self.terminal_state_cost_fn)
+
+ return costs
+
+ @staticmethod
+ def gradient_hamiltonian_x(x, u, lam):
+ """ gradient of hamitonian with respect to the state,
+ """
+ raise NotImplementedError("Implement gradient of hamitonian with respect to the state")
+
+ @staticmethod
+ def gradient_hamiltonian_u(x, u, lam):
+ """ gradient of hamitonian with respect to the input
+ """
+ raise NotImplementedError("Implement gradient of hamitonian with respect to the input")
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/ilqr.py b/PythonLinearNonlinearControl/controllers/ilqr.py
new file mode 100644
index 0000000..46eedac
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/ilqr.py
@@ -0,0 +1,24 @@
+from logging import getLogger
+
+import numpy as np
+import scipy.stats as stats
+
+from .controller import Controller
+from ..envs.cost import calc_cost
+
+logger = getLogger(__name__)
+
+class iLQR(Controller):
+ """ iterative Liner Quadratique Regulator
+ """
+ def __init__(self, config, model):
+ """
+ """
+ super(iLQR, self).__init__(config, model)
+
+ if config.TYPE != "Nonlinear":
+ raise ValueError("{} could be not applied to \
+ this controller".format(model))
+
+ self.model = model
+
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/make_controllers.py b/PythonLinearNonlinearControl/controllers/make_controllers.py
new file mode 100644
index 0000000..05a5f3b
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/make_controllers.py
@@ -0,0 +1,18 @@
+from .mpc import LinearMPC
+from .cem import CEM
+from .random import RandomShooting
+from .mppi import MPPI
+from .ilqr import iLQR
+
+def make_controller(args, config, model):
+
+ if args.controller_type == "MPC":
+ return LinearMPC(config, model)
+ elif args.controller_type == "CEM":
+ return CEM(config, model)
+ elif args.controller_type == "Random":
+ return RandomShooting(config, model)
+ elif args.controller_type == "MPPI":
+ return MPPI(config, model)
+ elif args.controller_type == "iLQR":
+ return iLQR(config, model)
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/mpc.py b/PythonLinearNonlinearControl/controllers/mpc.py
new file mode 100644
index 0000000..766973c
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/mpc.py
@@ -0,0 +1,217 @@
+from logging import getLogger
+
+import numpy as np
+from cvxopt import matrix, solvers
+
+from .controller import Controller
+from ..envs.cost import calc_cost
+
+logger = getLogger(__name__)
+
+class LinearMPC(Controller):
+ """ Model Predictive Controller for linear model
+
+ Attributes:
+ A (numpy.ndarray): system matrix, shape(state_size, state_size)
+ B (numpy.ndarray): input matrix, shape(state_size, input_size)
+ Q (numpy.ndarray): cost function weight for states
+ R (numpy.ndarray): cost function weight for states
+ history_us (list[numpy.ndarray]): time history of optimal input
+ Ref:
+ Maciejowski, J. M. (2002). Predictive control: with constraints.
+ """
+ def __init__(self, config, model):
+ """
+ Args:
+ model (Model): system matrix, shape(state_size, state_size)
+ config (ConfigModule): input matrix, shape(state_size, input_size)
+ """
+ if config.TYPE != "Linear":
+ raise ValueError("{} could be not applied to \
+ this controller".format(model))
+ super(LinearMPC, self).__init__(config, model)
+ # system parameters
+ self.model = model
+ self.A = model.A
+ self.B = model.B
+ self.state_size = config.STATE_SIZE
+ self.input_size = config.INPUT_SIZE
+ self.pred_len = config.PRED_LEN
+
+ # get cost func
+ self.state_cost_fn = config.state_cost_fn
+ self.terminal_state_cost_fn = config.terminal_state_cost_fn
+ self.input_cost_fn = config.input_cost_fn
+
+ # cost parameters
+ self.Q = config.Q
+ self.R = config.R
+ self.Qs = None
+ self.Rs = None
+
+ # constraints
+ self.dt_input_lower_bound = config.DT_INPUT_LOWER_BOUND
+ self.dt_input_upper_bound = config.DT_INPUT_UPPER_BOUND
+ self.input_lower_bound = config.INPUT_LOWER_BOUND
+ self.input_upper_bound = config.INPUT_UPPER_BOUND
+
+ # setup controllers
+ self.W = None
+ self.omega = None
+ self.F = None
+ self.f = None
+ self.setup()
+
+ # history
+ self.history_u = [np.zeros(self.input_size)]
+
+ def setup(self):
+ """
+ setup Model Predictive Control as a quadratic programming
+ """
+ A_factorials = [self.A]
+ self.phi_mat = self.A.copy()
+
+ for _ in range(self.pred_len - 1):
+ temp_mat = np.matmul(A_factorials[-1], self.A)
+ self.phi_mat = np.vstack((self.phi_mat, temp_mat))
+ A_factorials.append(temp_mat) # after we use this factorials
+
+ self.gamma_mat = self.B.copy()
+ gammma_mat_temp = self.B.copy()
+
+ for i in range(self.pred_len - 1):
+ temp_1_mat = np.matmul(A_factorials[i], self.B)
+ gammma_mat_temp = temp_1_mat + gammma_mat_temp
+ self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
+
+ self.theta_mat = self.gamma_mat.copy()
+
+ for i in range(self.pred_len - 1):
+ temp_mat = np.zeros_like(self.gamma_mat)
+ temp_mat[int((i + 1)*self.state_size): , :] =\
+ self.gamma_mat[:-int((i + 1)*self.state_size) , :]
+
+ self.theta_mat = np.hstack((self.theta_mat, temp_mat))
+
+ # evaluation function weight
+ diag_Qs = np.tile(np.diag(self.Q), self.pred_len)
+ diag_Rs = np.tile(np.diag(self.R), self.pred_len)
+ self.Qs = np.diag(diag_Qs)
+ self.Rs = np.diag(diag_Rs)
+
+ # constraints
+ # about inputs
+ if self.input_lower_bound is not None:
+ self.F = np.zeros((self.input_size * 2,
+ self.pred_len * self.input_size))
+
+ for i in range(self.input_size):
+ self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
+ temp_F = self.F.copy()
+
+ for i in range(self.pred_len - 1):
+ for j in range(self.input_size):
+ temp_F[j * 2: (j + 1) * 2,\
+ ((i+1) * self.input_size) + j] = np.array([1., -1.])
+ self.F = np.vstack((self.F, temp_F))
+
+ self.F1 = self.F[:, :self.input_size]
+
+ temp_f = []
+ for i in range(self.input_size):
+ temp_f.append(-1 * self.input_upper_bound[i])
+ temp_f.append(self.input_lower_bound[i])
+
+ self.f = np.tile(np.array(temp_f).flatten(), self.pred_len)
+
+ # about dt_input constraints
+ if self.dt_input_lower_bound is not None:
+ self.W = np.zeros((2, self.pred_len * self.input_size))
+ self.W[:, 0] = np.array([1., -1.])
+
+ for i in range(self.pred_len * self.input_size - 1):
+ temp_W = np.zeros((2, self.pred_len * self.input_size))
+ temp_W[:, i+1] = np.array([1., -1.])
+ self.W = np.vstack((self.W, temp_W))
+
+ temp_omega = []
+
+ for i in range(self.input_size):
+ temp_omega.append(self.dt_input_upper_bound[i])
+ temp_omega.append(-1. * self.dt_input_lower_bound[i])
+
+ self.omega = np.tile(np.array(temp_omega).flatten(),
+ self.pred_len)
+
+ def obtain_sol(self, curr_x, g_xs):
+ """ calculate the optimal inputs
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ g_xs (numpy.ndarrya): goal trajectory,
+ shape(plan_len+1, state_size)
+ Returns:
+ opt_input (numpy.ndarray): optimal input, shape(input_size, )
+ """
+ temp_1 = np.matmul(self.phi_mat, curr_x.reshape(-1, 1))
+ temp_2 = np.matmul(self.gamma_mat, self.history_u[-1].reshape(-1, 1))
+
+ error = g_xs[1:].reshape(-1, 1) - temp_1 - temp_2
+
+ G = np.matmul(self.theta_mat.T, np.matmul(self.Qs, error))
+
+ H = np.matmul(self.theta_mat.T, np.matmul(self.Qs, self.theta_mat)) \
+ + self.Rs
+ H = H * 0.5
+
+ # constraints
+ A = []
+ b = []
+
+ if self.W is not None:
+ A.append(self.W)
+ b.append(self.omega.reshape(-1, 1))
+
+ if self.F is not None:
+ b_F = - np.matmul(self.F1, self.history_u[-1].reshape(-1, 1)) \
+ - self.f.reshape(-1, 1)
+ A.append(self.F)
+ b.append(b_F)
+
+ A = np.array(A).reshape(-1, self.input_size * self.pred_len)
+
+ ub = np.array(b).flatten()
+
+ # make cvxpy problem formulation
+ P = 2*matrix(H)
+ q = matrix(-1 * G)
+ A = matrix(A)
+ b = matrix(ub)
+
+ # solve the problem
+ opt_result = solvers.qp(P, q, G=A, h=b)
+ opt_dt_us = np.array(list(opt_result['x']))
+ # to dt form
+ opt_dt_u_seq = np.cumsum(opt_dt_us.reshape(self.pred_len,\
+ self.input_size),
+ axis=0)
+
+ opt_u_seq = opt_dt_u_seq + self.history_u[-1]
+
+ # save
+ self.history_u.append(opt_u_seq[0])
+
+ # check costs
+ costs = self.calc_cost(curr_x,
+ opt_u_seq.reshape(1,
+ self.pred_len,
+ self.input_size),
+ g_xs)
+
+ logger.debug("Cost = {}".format(costs))
+
+ return opt_u_seq[0]
+
+ def __str__(self):
+ return "LinearMPC"
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/mppi.py b/PythonLinearNonlinearControl/controllers/mppi.py
new file mode 100644
index 0000000..fc8d887
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/mppi.py
@@ -0,0 +1,124 @@
+from logging import getLogger
+
+import numpy as np
+import scipy.stats as stats
+
+from .controller import Controller
+from ..envs.cost import calc_cost
+
+logger = getLogger(__name__)
+
+class MPPI(Controller):
+ """ Model Predictive Path Integral for linear and nonlinear method
+
+ Attributes:
+ history_u (list[numpy.ndarray]): time history of optimal input
+ Ref:
+ Nagabandi, A., Konoglie, K., Levine, S., & Kumar, V. (2019).
+ Deep Dynamics Models for Learning Dexterous Manipulation.
+ arXiv preprint arXiv:1909.11652.
+ """
+ def __init__(self, config, model):
+ super(MPPI, self).__init__(config, model)
+
+ # model
+ self.model = model
+
+ # general parameters
+ self.pred_len = config.PRED_LEN
+ self.input_size = config.INPUT_SIZE
+
+ # mppi parameters
+ self.beta = config.opt_config["MPPI"]["beta"]
+ self.pop_size = config.opt_config["MPPI"]["popsize"]
+ self.kappa = config.opt_config["MPPI"]["kappa"]
+ self.noise_sigma = config.opt_config["MPPI"]["noise_sigma"]
+ self.opt_dim = self.input_size * self.pred_len
+
+ # get bound
+ self.input_upper_bounds = np.tile(config.INPUT_UPPER_BOUND,
+ (self.pred_len, 1))
+ self.input_lower_bounds = np.tile(config.INPUT_LOWER_BOUND,
+ (self.pred_len, 1))
+
+ # get cost func
+ self.state_cost_fn = config.state_cost_fn
+ self.terminal_state_cost_fn = config.terminal_state_cost_fn
+ self.input_cost_fn = config.input_cost_fn
+
+ # init mean
+ self.prev_sol = np.tile((config.INPUT_UPPER_BOUND \
+ + config.INPUT_LOWER_BOUND) / 2.,
+ self.pred_len)
+ self.prev_sol = self.prev_sol.reshape(self.pred_len, self.input_size)
+
+ # save
+ self.history_u = [np.zeros(self.input_size)]
+
+ def clear_sol(self):
+ """ clear prev sol
+ """
+ logger.debug("Clear Solution")
+ self.prev_sol = \
+ (self.input_upper_bounds + self.input_lower_bounds) / 2.
+ self.prev_sol = self.prev_sol.reshape(self.pred_len, self.input_size)
+
+ def obtain_sol(self, curr_x, g_xs):
+ """ calculate the optimal inputs
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ g_xs (numpy.ndarrya): goal trajectory, shape(plan_len, state_size)
+ Returns:
+ opt_input (numpy.ndarray): optimal input, shape(input_size, )
+ """
+ # get noised inputs
+ noise = np.random.normal(
+ loc=0, scale=1.0, size=(self.pop_size, self.pred_len,
+ self.input_size)) * self.noise_sigma
+ noised_inputs = noise.copy()
+
+ for t in range(self.pred_len):
+ if t > 0:
+ noised_inputs[:, t, :] = self.beta \
+ * (self.prev_sol[t, :] \
+ + noise[:, t, :]) \
+ + (1 - self.beta) \
+ * noised_inputs[:, t-1, :]
+ else:
+ noised_inputs[:, t, :] = self.beta \
+ * (self.prev_sol[t, :] \
+ + noise[:, t, :]) \
+ + (1 - self.beta) \
+ * self.history_u[-1]
+
+ # clip actions
+ noised_inputs = np.clip(
+ noised_inputs, self.input_lower_bounds, self.input_upper_bounds)
+
+ # calc cost
+ costs = self.calc_cost(curr_x, noised_inputs, g_xs)
+ rewards = -costs
+
+ # mppi update
+ # normalize and get sum of reward
+ # exp_rewards.shape = (N, )
+ exp_rewards = np.exp(self.kappa * (rewards - np.max(rewards)))
+ denom = np.sum(exp_rewards) + 1e-10 # avoid numeric error
+
+ # weight actions
+ weighted_inputs = exp_rewards[:, np.newaxis, np.newaxis] \
+ * noised_inputs
+ sol = np.sum(weighted_inputs, 0) / denom
+
+ # update
+ self.prev_sol[:-1] = sol[1:]
+ self.prev_sol[-1] = sol[-1] # last use the terminal input
+
+ # log
+ self.history_u.append(sol[0])
+
+ return sol[0]
+
+ def __str__(self):
+ return "MPPI"
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/controllers/random.py b/PythonLinearNonlinearControl/controllers/random.py
new file mode 100644
index 0000000..53a7622
--- /dev/null
+++ b/PythonLinearNonlinearControl/controllers/random.py
@@ -0,0 +1,77 @@
+from logging import getLogger
+
+import numpy as np
+import scipy.stats as stats
+
+from .controller import Controller
+from ..envs.cost import calc_cost
+
+logger = getLogger(__name__)
+
+class RandomShooting(Controller):
+ """ Random Shooting Method for linear and nonlinear method
+
+ Attributes:
+ history_u (list[numpy.ndarray]): time history of optimal input
+ Ref:
+ Chua, K., Calandra, R., McAllister, R., & Levine, S. (2018).
+ Deep reinforcement learning in a handful of trials
+ using probabilistic dynamics models.
+ In Advances in Neural Information Processing Systems (pp. 4754-4765).
+ """
+ def __init__(self, config, model):
+ super(RandomShooting, self).__init__(config, model)
+
+ # model
+ self.model = model
+
+ # general parameters
+ self.pred_len = config.PRED_LEN
+ self.input_size = config.INPUT_SIZE
+
+ # cem parameters
+ self.pop_size = config.opt_config["Random"]["popsize"]
+ self.opt_dim = self.input_size * self.pred_len
+
+ # get bound
+ self.input_upper_bounds = np.tile(config.INPUT_UPPER_BOUND,
+ self.pred_len)
+ self.input_lower_bounds = np.tile(config.INPUT_LOWER_BOUND,
+ self.pred_len)
+
+ # get cost func
+ self.state_cost_fn = config.state_cost_fn
+ self.terminal_state_cost_fn = config.terminal_state_cost_fn
+ self.input_cost_fn = config.input_cost_fn
+
+ # save
+ self.history_u = []
+
+ def obtain_sol(self, curr_x, g_xs):
+ """ calculate the optimal inputs
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ g_xs (numpy.ndarrya): goal trajectory, shape(plan_len, state_size)
+ Returns:
+ opt_input (numpy.ndarray): optimal input, shape(input_size, )
+ """
+ # set different seed
+ np.random.seed()
+
+ samples = np.random.uniform(self.input_lower_bounds,
+ self.input_upper_bounds,
+ [self.pop_size, self.opt_dim])
+ # calc cost
+ costs = self.calc_cost(curr_x,
+ samples.reshape(self.pop_size,
+ self.pred_len,
+ self.input_size),
+ g_xs)
+ # solution
+ sol = samples[np.argmin(costs)]
+
+ return sol.reshape(self.pred_len, self.input_size).copy()[0]
+
+ def __str__(self):
+ return "RandomShooting"
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/envs/__init__.py b/PythonLinearNonlinearControl/envs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/envs/cost.py b/PythonLinearNonlinearControl/envs/cost.py
new file mode 100644
index 0000000..5d10697
--- /dev/null
+++ b/PythonLinearNonlinearControl/envs/cost.py
@@ -0,0 +1,37 @@
+from logging import getLogger
+
+import numpy as np
+
+logger = getLogger(__name__)
+
+def calc_cost(pred_xs, input_sample, g_xs,
+ state_cost_fn, input_cost_fn, terminal_state_cost_fn):
+ """ calculate the cost
+
+ Args:
+ pred_xs (numpy.ndarray): predicted state trajectory,
+ shape(pop_size, pred_len+1, state_size)
+ input_sample (numpy.ndarray): inputs samples trajectory,
+ shape(pop_size, pred_len+1, input_size)
+ g_xs (numpy.ndarray): goal state trajectory,
+ shape(pop_size, pred_len+1, state_size)
+ state_cost_fn (function): state cost fucntion
+ input_cost_fn (function): input cost fucntion
+ terminal_state_cost_fn (function): terminal state cost fucntion
+ Returns:
+ cost (numpy.ndarray): cost of the input sample, shape(pop_size, )
+ """
+ # state cost
+ state_pred_par_cost = state_cost_fn(pred_xs[:, 1:-1, :], g_xs[:, 1:-1, :])
+ state_cost = np.sum(np.sum(state_pred_par_cost, axis=-1), axis=-1)
+
+ # terminal cost
+ terminal_state_par_cost = terminal_state_cost_fn(pred_xs[:, -1, :],
+ g_xs[:, -1, :])
+ terminal_state_cost = np.sum(terminal_state_par_cost, axis=-1)
+
+ # act cost
+ act_pred_par_cost = input_cost_fn(input_sample)
+ act_cost = np.sum(np.sum(act_pred_par_cost, axis=-1), axis=-1)
+
+ return state_cost + terminal_state_cost + act_cost
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/envs/env.py b/PythonLinearNonlinearControl/envs/env.py
new file mode 100644
index 0000000..c8ace4b
--- /dev/null
+++ b/PythonLinearNonlinearControl/envs/env.py
@@ -0,0 +1,54 @@
+import numpy as np
+
+class Env():
+ """
+ Attributes:
+ curr_x (numpy.ndarray): current state
+ history_x (list[numpy.ndarray]): historty of state, shape(step_count*state_size)
+ step_count (int): step count
+ """
+ def __init__(self, config):
+ """
+ """
+ self.config = config
+ self.curr_x = None
+ self.goal_state = None
+ self.history_x = []
+ self.history_g_x = []
+ self.step_count = None
+
+ def reset(self, init_x=None):
+ """ reset state
+ Returns:
+ init_x (numpy.ndarray): initial state, shape(state_size, )
+ info (dict): information
+ """
+ self.step_count = 0
+
+ self.curr_x = np.zeros(self.config["state_size"])
+
+ if init_x is not None:
+ self.curr_x = init_x
+
+ # clear memory
+ self.history_x = []
+ self.history_g_x = []
+
+ return self.curr_x, {}
+
+ def step(self, u):
+ """
+ Args:
+ u (numpy.ndarray) : input, shape(input_size, )
+ Returns:
+ next_x (numpy.ndarray): next state, shape(state_size, )
+ cost (float): costs
+ done (bool): end the simulation or not
+ info (dict): information
+ """
+ raise NotImplementedError("Implement step function")
+
+ def __str__(self):
+ """
+ """
+ return self.config
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/envs/first_order_lag.py b/PythonLinearNonlinearControl/envs/first_order_lag.py
new file mode 100644
index 0000000..0348ee0
--- /dev/null
+++ b/PythonLinearNonlinearControl/envs/first_order_lag.py
@@ -0,0 +1,113 @@
+import numpy as np
+import scipy
+from scipy import integrate
+from .env import Env
+
+class FirstOrderLagEnv(Env):
+ """ First Order Lag System Env
+ """
+ def __init__(self, tau=0.63):
+ """
+ """
+ self.config = {"state_size" : 4,\
+ "input_size" : 2,\
+ "dt" : 0.05,\
+ "max_step" : 500,\
+ "input_lower_bound": [-0.5, -0.5],\
+ "input_upper_bound": [0.5, 0.5],
+ }
+
+ super(FirstOrderLagEnv, self).__init__(self.config)
+
+ # to get discrete system matrix
+ self.A, self.B = self._to_state_space(tau, dt=self.config["dt"])
+
+ @staticmethod
+ def _to_state_space(tau, dt=0.05):
+ """
+ Args:
+ tau (float): time constant
+ dt (float): discrte time
+ Returns:
+ A (numpy.ndarray): discrete A matrix
+ B (numpy.ndarray): discrete B matrix
+ """
+ # continuous
+ Ac = np.array([[-1./tau, 0., 0., 0.],
+ [0., -1./tau, 0., 0.],
+ [1., 0., 0., 0.],
+ [0., 1., 0., 0.]])
+ Bc = np.array([[1./tau, 0.],
+ [0., 1./tau],
+ [0., 0.],
+ [0., 0.]])
+ # to discrete system
+ A = scipy.linalg.expm(dt*Ac)
+ # B = np.matmul(np.matmul(scipy.linalg.expm(Ac*dt) -
+ # scipy.linalg.expm(Ac*0.), np.linalg.inv(Ac)),\
+ # Bc)
+ B = np.zeros_like(Bc)
+ for m in range(Bc.shape[0]):
+ for n in range(Bc.shape[1]):
+ integrate_fn =\
+ lambda tau: np.matmul(scipy.linalg.expm(Ac*tau), Bc)[m, n]
+ sol = integrate.quad(integrate_fn, 0, dt)
+ B[m, n] = sol[0]
+
+ return A, B
+
+ def reset(self, init_x=None):
+ """ reset state
+ Returns:
+ init_x (numpy.ndarray): initial state, shape(state_size, )
+ info (dict): information
+ """
+ self.step_count = 0
+
+ self.curr_x = np.zeros(self.config["state_size"])
+
+ if init_x is not None:
+ self.curr_x = init_x
+
+ # goal
+ self.goal_state = np.array([0., 0, -2., 3.])
+
+ # clear memory
+ self.history_x = []
+ self.history_g_x = []
+
+ return self.curr_x, {"goal_state": self.goal_state}
+
+ def step(self, u):
+ """
+ Args:
+ u (numpy.ndarray) : input, shape(input_size, )
+ Returns:
+ next_x (numpy.ndarray): next state, shape(state_size, )
+ cost (float): costs
+ done (bool): end the simulation or not
+ info (dict): information
+ """
+ # clip action
+ u = np.clip(u,
+ self.config["input_lower_bound"],
+ self.config["input_lower_bound"])
+
+ next_x = np.matmul(self.A, self.curr_x[:, np.newaxis]) \
+ + np.matmul(self.B, u[:, np.newaxis])
+
+ # cost
+ cost = 0
+ cost = np.sum(u**2)
+ cost += np.sum((self.curr_x-g_x)**2)
+
+ # save history
+ self.history_x.append(next_x.flatten())
+ self.history_g_x.append(self.goal_state.flatten())
+
+ # update
+ self.curr_x = next_x.flatten()
+ # update costs
+ self.step_count += 1
+
+ return next_x.flatten(), cost, self.step_count > self.config["max_step"], {"goal_state" : self.goal_state}
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/envs/make_envs.py b/PythonLinearNonlinearControl/envs/make_envs.py
new file mode 100644
index 0000000..aedd299
--- /dev/null
+++ b/PythonLinearNonlinearControl/envs/make_envs.py
@@ -0,0 +1,8 @@
+from .first_order_lag import FirstOrderLagEnv
+
+def make_env(args):
+
+ if args.env == "FirstOrderLag":
+ return FirstOrderLagEnv()
+
+ raise NotImplementedError("There is not {} Env".format(name))
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/envs/two_wheeled.py b/PythonLinearNonlinearControl/envs/two_wheeled.py
new file mode 100644
index 0000000..55f08f6
--- /dev/null
+++ b/PythonLinearNonlinearControl/envs/two_wheeled.py
@@ -0,0 +1,145 @@
+import numpy as np
+import scipy
+from scipy import integrate
+from .env import Env
+
+class TwoWheeledConstEnv(Env):
+ """ Two wheeled robot with constant goal Env
+ """
+ def __init__(self):
+ """
+ """
+ self.config = {"state_size" : 3,\
+ "input_size" : 2,\
+ "dt" : 0.01,\
+ "max_step" : 500,\
+ "input_lower_bound": [-1.5, -3.14],\
+ "input_upper_bound": [1.5, 3.14],
+ }
+
+ super(TwoWheeledEnv, self).__init__(self.config)
+
+ def reset(self, init_x=None):
+ """ reset state
+ Returns:
+ init_x (numpy.ndarray): initial state, shape(state_size, )
+ info (dict): information
+ """
+ self.step_count = 0
+
+ self.curr_x = np.zeros(self.config["state_size"])
+
+ if init_x is not None:
+ self.curr_x = init_x
+
+ # goal
+ self.goal_state = np.array([0., 0, -2., 3.])
+
+ # clear memory
+ self.history_x = []
+ self.history_g_x = []
+
+ return self.curr_x, {"goal_state": self.goal_state}
+
+ def step(self, u):
+ """
+ Args:
+ u (numpy.ndarray) : input, shape(input_size, )
+ Returns:
+ next_x (numpy.ndarray): next state, shape(state_size, )
+ cost (float): costs
+ done (bool): end the simulation or not
+ info (dict): information
+ """
+ # clip action
+ u = np.clip(u,
+ self.config["input_lower_bound"],
+ self.config["input_lower_bound"])
+
+ # step
+ next_x = np.matmul(self.A, self.curr_x[:, np.newaxis]) \
+ + np.matmul(self.B, u[:, np.newaxis])
+
+ # TODO: implement costs
+
+ # save history
+ self.history_x.append(next_x.flatten())
+ self.history_g_x.append(self.goal_state.flatten())
+
+ # update
+ self.curr_x = next_x.flatten()
+ # update costs
+ self.step_count += 1
+
+ return next_x.flatten(), 0., self.step_count > self.config["max_step"], {"goal_state" : self.goal_state}
+
+class TwoWheeledEnv(Env):
+ """ Two wheeled robot Env
+ """
+ def __init__(self):
+ """
+ """
+ self.config = {"state_size" : 3,\
+ "input_size" : 2,\
+ "dt" : 0.01,\
+ "max_step" : 500,\
+ "input_lower_bound": [-1.5, -3.14],\
+ "input_upper_bound": [1.5, 3.14],
+ }
+
+ super(TwoWheeledEnv, self).__init__(self.config)
+
+ def reset(self, init_x=None):
+ """ reset state
+ Returns:
+ init_x (numpy.ndarray): initial state, shape(state_size, )
+ info (dict): information
+ """
+ self.step_count = 0
+
+ self.curr_x = np.zeros(self.config["state_size"])
+
+ if init_x is not None:
+ self.curr_x = init_x
+
+ # goal
+ self.goal_state = np.array([0., 0, -2., 3.])
+
+ # clear memory
+ self.history_x = []
+ self.history_g_x = []
+
+ return self.curr_x, {"goal_state": self.goal_state}
+
+ def step(self, u):
+ """
+ Args:
+ u (numpy.ndarray) : input, shape(input_size, )
+ Returns:
+ next_x (numpy.ndarray): next state, shape(state_size, )
+ cost (float): costs
+ done (bool): end the simulation or not
+ info (dict): information
+ """
+ # clip action
+ u = np.clip(u,
+ self.config["input_lower_bound"],
+ self.config["input_lower_bound"])
+
+ # step
+ next_x = np.matmul(self.A, self.curr_x[:, np.newaxis]) \
+ + np.matmul(self.B, u[:, np.newaxis])
+
+ # TODO: implement costs
+
+ # save history
+ self.history_x.append(next_x.flatten())
+ self.history_g_x.append(self.goal_state.flatten())
+
+ # update
+ self.curr_x = next_x.flatten()
+ # update costs
+ self.step_count += 1
+
+ return next_x.flatten(), 0., self.step_count > self.config["max_step"], {"goal_state" : self.goal_state}
+
diff --git a/PythonLinearNonlinearControl/helper.py b/PythonLinearNonlinearControl/helper.py
new file mode 100644
index 0000000..7fa2058
--- /dev/null
+++ b/PythonLinearNonlinearControl/helper.py
@@ -0,0 +1,147 @@
+import argparse
+import datetime
+import json
+import os
+import sys
+import six
+import pickle
+from logging import DEBUG, basicConfig, getLogger, FileHandler, StreamHandler, Formatter, Logger
+
+def make_logger(save_dir):
+ """
+ Args:
+ save_dir (str): save directory
+ """
+ # base config setting
+ basicConfig(
+ format='[%(asctime)s] %(name)s %(levelname)s: %(message)s',
+ datefmt='%Y-%m-%d %H:%M:%S'
+ )
+
+ # mypackage log level
+ logger = getLogger("PythonLinearNonlinearControl")
+ logger.setLevel(DEBUG)
+
+ # file handler
+ log_path = os.path.join(save_dir, "log.txt")
+ file_handler = FileHandler(log_path)
+ file_handler.setLevel(DEBUG)
+ file_handler.setFormatter(Formatter('%(message)s'))
+ logger.addHandler(file_handler)
+
+ # sh handler
+ # sh_handler = StreamHandler()
+ # logger.addHandler(sh_handler)
+
+def int_tuple(s):
+ """ transform str to tuple
+ Args:
+ s (str): strings that you want to change
+ Returns:
+ tuple
+ """
+ return tuple(int(i) for i in s.split(','))
+
+def bool_flag(s):
+ """ transform str to bool flg
+ Args:
+ s (str): strings that you want to change
+ """
+ if s == '1':
+ return True
+ elif s == '0':
+ return False
+ msg = 'Invalid value "%s" for bool flag (should be 0 or 1)'
+ raise ValueError(msg % s)
+
+def file_exists(path):
+ """ Check file existence on given path
+ Args:
+ path (str): path of the file to check existence
+ Returns:
+ file_existence (bool): True if file exists otherwise False
+ """
+ return os.path.exists(path)
+
+def create_dir_if_not_exist(outdir):
+ """ Check directory existence and creates new directory if not exist
+ Args:
+ outdir (str): path of the file to create directory
+ RuntimeError:
+ file exists in outdir but it is not a directory
+ """
+ if file_exists(outdir):
+ if not os.path.isdir(outdir):
+ raise RuntimeError('{} is not a directory'.format(outdir))
+ else:
+ return
+ os.makedirs(outdir)
+
+def write_text_to_file(file_path, data):
+ """ Write given text data to file
+ Args:
+ file_path (str): path of the file to write data
+ data (str): text to write to the file
+ """
+ with open(file_path, 'w') as f:
+ f.write(data)
+
+def read_text_from_file(file_path):
+ """ Read given file as text
+ Args:
+ file_path (str): path of the file to read data
+ Returns
+ data (str): text read from the file
+ """
+ with open(file_path, 'r') as f:
+ return f.read()
+
+def save_pickle(file_path, data):
+ """ pickle given data to file
+ Args:
+ file_path (str): path of the file to pickle data
+ data (): data to pickle
+ """
+ with open(file_path, 'wb') as f:
+ pickle.dump(data, f)
+
+def load_pickle(file_path):
+ """ load pickled data from file
+ Args:
+ file_path (str): path of the file to load pickled data
+ Returns:
+ data (): data pickled in file
+ """
+ with open(file_path, 'rb') as f:
+ if six.PY2:
+ return pickle.load(f)
+ else:
+ return pickle.load(f, encoding='bytes')
+
+def prepare_output_dir(base_dir, args, time_format='%Y-%m-%d-%H%M%S'):
+ """ prepare a directory with current datetime as name.
+ created directory contains the command and args when the script was called as text file.
+ Args:
+ base_dir (str): path of the directory to save data
+ args (dict): arguments when the python script was called
+ time_format (str): datetime format string for naming directory to save data
+ Returns:
+ out_dir (str): directory to save data
+ """
+ time_str = datetime.datetime.now().strftime(time_format)
+ outdir = os.path.join(base_dir, time_str)
+
+ create_dir_if_not_exist(outdir)
+
+ # Save all the arguments
+ args_file_path = os.path.join(outdir, 'args.txt')
+ if isinstance(args, argparse.Namespace):
+ args = vars(args)
+ write_text_to_file(args_file_path, json.dumps(args))
+
+ # Save the command
+ argv_file_path = os.path.join(outdir, 'command.txt')
+ argv = ' '.join(sys.argv)
+ write_text_to_file(argv_file_path, argv)
+
+ return outdir
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/models/__init__.py b/PythonLinearNonlinearControl/models/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/models/first_order_lag.py b/PythonLinearNonlinearControl/models/first_order_lag.py
new file mode 100644
index 0000000..a4a97fb
--- /dev/null
+++ b/PythonLinearNonlinearControl/models/first_order_lag.py
@@ -0,0 +1,51 @@
+import numpy as np
+import scipy.linalg
+from scipy import integrate
+from .model import LinearModel
+
+class FirstOrderLagModel(LinearModel):
+ """ first order lag model
+ Attributes:
+ curr_x (numpy.ndarray):
+ u (numpy.ndarray):
+ history_pred_xs (numpy.ndarray):
+ """
+ def __init__(self, config, tau=0.63):
+ """
+ Args:
+ tau (float): time constant
+ """
+ # param
+ self.A, self.B = self._to_state_space(tau, dt=config.DT) # discrete system
+ super(FirstOrderLagModel, self).__init__(self.A, self.B)
+
+ @staticmethod
+ def _to_state_space(tau, dt=0.05):
+ """
+ Args:
+ tau (float): time constant
+ dt (float): discrte time
+ Returns:
+ A (numpy.ndarray): discrete A matrix
+ B (numpy.ndarray): discrete B matrix
+ """
+ # continuous
+ Ac = np.array([[-1./tau, 0., 0., 0.],
+ [0., -1./tau, 0., 0.],
+ [1., 0., 0., 0.],
+ [0., 1., 0., 0.]])
+ Bc = np.array([[1./tau, 0.],
+ [0., 1./tau],
+ [0., 0.],
+ [0., 0.]])
+ # to discrete system
+ A = scipy.linalg.expm(dt*Ac)
+ # B = np.matmul(np.matmul(scipy.linalg.expm(Ac*dt)-scipy.linalg.expm(Ac*0.), np.linalg.inv(Ac)), Bc)
+ B = np.zeros_like(Bc)
+ for m in range(Bc.shape[0]):
+ for n in range(Bc.shape[1]):
+ integrate_fn = lambda tau: np.matmul(scipy.linalg.expm(Ac*tau), Bc)[m, n]
+ sol = integrate.quad(integrate_fn, 0, dt)
+ B[m, n] = sol[0]
+
+ return A, B
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/models/make_models.py b/PythonLinearNonlinearControl/models/make_models.py
new file mode 100644
index 0000000..73c3987
--- /dev/null
+++ b/PythonLinearNonlinearControl/models/make_models.py
@@ -0,0 +1,8 @@
+from .first_order_lag import FirstOrderLagModel
+
+def make_model(args, config):
+
+ if args.env == "FirstOrderLag":
+ return FirstOrderLagModel(config)
+
+ raise NotImplementedError("There is not {} Model".format(args.env))
diff --git a/PythonLinearNonlinearControl/models/model.py b/PythonLinearNonlinearControl/models/model.py
new file mode 100644
index 0000000..27bbd34
--- /dev/null
+++ b/PythonLinearNonlinearControl/models/model.py
@@ -0,0 +1,190 @@
+import numpy as np
+
+class Model():
+ """ base class of model
+ """
+ def __init__(self):
+ """
+ """
+ pass
+
+ def predict_traj(self, curr_x, us):
+ """ predict trajectories
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ us (numpy.ndarray): inputs,
+ shape(pred_len, input_size)
+ or shape(pop_size, pred_len, input_size)
+ Returns:
+ pred_xs (numpy.ndarray): predicted state,
+ shape(pred_len+1, state_size) including current state
+ or shape(pop_size, pred_len+1, state_size)
+ """
+ if len(us.shape) == 3:
+ pred_xs =self._predict_traj_alltogether(curr_x, us)
+ elif len(us.shape) == 2:
+ pred_xs = self._predict_traj(curr_x, us)
+ else:
+ raise ValueError("Invalid us")
+
+ return pred_xs
+
+ def _predict_traj(self, curr_x, us):
+ """ predict trajectories
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, )
+ us (numpy.ndarray): inputs, shape(pred_len, input_size)
+ Returns:
+ pred_xs (numpy.ndarray): predicted state,
+ shape(pred_len+1, state_size) including current state
+ """
+ # get size
+ pred_len = us.shape[0]
+ # initialze
+ x = curr_x
+ pred_xs = curr_x[np.newaxis, :]
+
+ for t in range(pred_len):
+ next_x = self.predict_next_state(x, us[t])
+ # update
+ pred_xs = np.concatenate((pred_xs, next_x[np.newaxis, :]), axis=0)
+ x = next_x
+
+ return pred_xs
+
+ def _predict_traj_alltogether(self, curr_x, us):
+ """ predict trajectories for all samples
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(pop_size, state_size)
+ us (numpy.ndarray): inputs, shape(pop_size, pred_len, input_size)
+ Returns:
+ pred_xs (numpy.ndarray): predicted state,
+ shape(pop_size, pred_len+1, state_size) including current state
+ """
+ # get size
+ (pop_size, pred_len, _) = us.shape
+ us = np.transpose(us, (1, 0, 2)) # to (pred_len, pop_size, input_size)
+ # initialze
+ x = np.tile(curr_x, (pop_size, 1))
+ pred_xs = x[np.newaxis, :, :] # (1, pop_size, state_size)
+
+ for t in range(pred_len):
+ # next_x.shape = (pop_size, state_size)
+ next_x = self.predict_next_state(x, us[t])
+ # update
+ pred_xs = np.concatenate((pred_xs, next_x[np.newaxis, :, :]),\
+ axis=0)
+ x = next_x
+
+ return np.transpose(pred_xs, (1, 0, 2))
+
+ def predict_next_state(self, curr_x, u):
+ """ predict next state
+ """
+ raise NotImplementedError("Implement the model")
+
+ def predict_adjoint_traj(self, xs, us, g_xs):
+ """
+ Args:
+ xs (numpy.ndarray): states trajectory, shape(pred_len+1, state_size)
+ us (numpy.ndarray): inputs, shape(pred_len, input_size)
+ g_xs (numpy.ndarray): goal states, shape(pred_len+1, state_size)
+ Returns:
+ lams (numpy.ndarray): adjoint state, shape(pred_len, state_size),
+ adjoint size is the same as state_size
+ """
+ # get size
+ (pred_len, input_size) = us.shape
+ # pred final adjoint state
+ lam = self.predict_terminal_adjoint_state(xs[-1],\
+ terminal_g_x=g_xs[-1])
+ lams = lam[np.newaxis, :]
+
+ for t in range(pred_len-1, 0, -1):
+ prev_lam = \
+ self.predict_adjoint_state(lam, xs[t], us[t],\
+ goal=g_xs[t], t=t)
+ # update
+ lams = np.concatenate((prev_lam[np.newaxis, :], lams), axis=0)
+ lam = prev_lam
+
+ return lams
+
+ def predict_adjoint_state(self, lam, x, u, goal=None, t=None):
+ """ predict adjoint states
+
+ Args:
+ lam (numpy.ndarray): adjoint state, shape(state_size, )
+ x (numpy.ndarray): state, shape(state_size, )
+ u (numpy.ndarray): input, shape(input_size, )
+ goal (numpy.ndarray): goal state, shape(state_size, )
+ Returns:
+ prev_lam (numpy.ndarrya): previous adjoint state,
+ shape(state_size, )
+ """
+ raise NotImplementedError("Implement the adjoint model")
+
+ def predict_terminal_adjoint_state(self, terminal_x, terminal_g_x=None):
+ """ predict terminal adjoint state
+
+ Args:
+ terminal_x (numpy.ndarray): terminal state, shape(state_size, )
+ terminal_g_x (numpy.ndarray): terminal goal state,
+ shape(state_size, )
+ Returns:
+ terminal_lam (numpy.ndarray): terminal adjoint state,
+ shape(state_size, )
+ """
+ raise NotImplementedError("Implement terminal adjoint state")
+
+ def gradient_x(self, x, u):
+ """ gradient of model with respect to the state
+ """
+ raise NotImplementedError("Implement gradient of model \
+ with respect to the state")
+
+ def gradient_u(self, x, u):
+ """ gradient of model with respect to the input
+ """
+ raise NotImplementedError("Implement gradient of model \
+ with respect to the input")
+
+class LinearModel(Model):
+ """ discrete linear model, x[k+1] = Ax[k] + Bu[k]
+
+ Attributes:
+ A (numpy.ndarray): shape(state_size, state_size)
+ B (numpy.ndarray): shape(state_size, input_size)
+ """
+ def __init__(self, A, B):
+ """
+ """
+ super(LinearModel, self).__init__()
+ self.A = A
+ self.B = B
+
+ def predict_next_state(self, curr_x, u):
+ """ predict next state
+
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size, ) or
+ shape(pop_size, state_size)
+ u (numpy.ndarray): input, shape(input_size, ) or
+ shape(pop_size, input_size)
+ Returns:
+ next_x (numpy.ndarray): next state, shape(state_size, ) or
+ shape(pop_size, state_size)
+ """
+ if len(u.shape) == 1:
+ next_x = np.matmul(self.A, curr_x[:, np.newaxis]) \
+ + np.matmul(self.B, u[:, np.newaxis])
+
+ return next_x.flatten()
+
+ elif len(u.shape) == 2:
+ next_x = np.matmul(curr_x, self.A.T) + np.matmul(u, self.B.T)
+
+ return next_x
diff --git a/PythonLinearNonlinearControl/planners/__init__.py b/PythonLinearNonlinearControl/planners/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/planners/const_planner.py b/PythonLinearNonlinearControl/planners/const_planner.py
new file mode 100644
index 0000000..5806c62
--- /dev/null
+++ b/PythonLinearNonlinearControl/planners/const_planner.py
@@ -0,0 +1,23 @@
+import numpy as np
+from .planner import Planner
+
+class ConstantPlanner():
+ """ This planner make constant goal state
+ """
+ def __init__(self, config):
+ """
+ """
+ super(ConstantPlanner, self).__init__()
+ self.pred_len = config.PRED_LEN
+ self.state_size = config.STATE_SIZE
+
+ def plan(self, curr_x, g_x=None):
+ """
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size)
+ g_x (numpy.ndarray): goal state, shape(state_size),
+ this state should be obtained from env
+ Returns:
+ g_xs (numpy.ndarrya): goal state, shape(pred_len, state_size)
+ """
+ return np.tile(g_x, (self.pred_len+1, 1))
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/planners/make_planners.py b/PythonLinearNonlinearControl/planners/make_planners.py
new file mode 100644
index 0000000..9da7f31
--- /dev/null
+++ b/PythonLinearNonlinearControl/planners/make_planners.py
@@ -0,0 +1,8 @@
+from .const_planner import ConstantPlanner
+
+def make_planner(args, config):
+
+ if args.planner_type == "const":
+ return ConstantPlanner(config)
+
+ raise NotImplementedError("There is not {} Planner".format(args.planner_type))
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/planners/planner.py b/PythonLinearNonlinearControl/planners/planner.py
new file mode 100644
index 0000000..7e20b4f
--- /dev/null
+++ b/PythonLinearNonlinearControl/planners/planner.py
@@ -0,0 +1,18 @@
+import numpy as np
+
+class Planner():
+ """
+ """
+ def __init__(self):
+ """
+ """
+ pass
+
+ def plan(self, curr_x):
+ """
+ Args:
+ curr_x (numpy.ndarray): current state, shape(state_size)
+ Returns:
+ g_xs (numpy.ndarrya): goal state, shape(pred_len, state_size)
+ """
+ raise NotImplementedError("Implement plan func")
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/plotters/__init__.py b/PythonLinearNonlinearControl/plotters/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/plotters/plot_func.py b/PythonLinearNonlinearControl/plotters/plot_func.py
new file mode 100644
index 0000000..216788e
--- /dev/null
+++ b/PythonLinearNonlinearControl/plotters/plot_func.py
@@ -0,0 +1,60 @@
+import os
+
+import numpy as np
+import matplotlib.pyplot as plt
+
+def plot_result(history, history_g=None, ylabel="x",
+ save_dir="./result", name="state_history"):
+ """
+ Args:
+ history (numpy.ndarray): history, shape(iters, size)
+ """
+ (iters, size) = history.shape
+ for i in range(0, size, 3):
+
+ figure = plt.figure()
+ axis1 = figure.add_subplot(311)
+ axis2 = figure.add_subplot(312)
+ axis3 = figure.add_subplot(313)
+
+ axis1.set_ylabel(ylabel + "_{}".format(i))
+ axis2.set_ylabel(ylabel + "_{}".format(i+1))
+ axis3.set_ylabel(ylabel + "_{}".format(i+2))
+ axis3.set_xlabel("time steps")
+
+ # gt
+ def plot(axis, history, history_g=None):
+ axis.plot(range(iters), history, c="r", linewidth=3)
+ if history_g is not None:
+ axis.plot(range(iters), history_g,\
+ c="b", linewidth=3, label="goal")
+
+ if i < size:
+ plot(axis1, history[:, i], history_g=history_g[:, i])
+ if i+1 < size:
+ plot(axis2, history[:, i+1], history_g=history_g[:, i+1])
+ if i+2 < size:
+ plot(axis3, history[:, i+2], history_g=history_g[:, i+2])
+
+ # save
+ if save_dir is not None:
+ path = os.path.join(save_dir, name + "-{}".format(i))
+ else:
+ path = name
+
+ axis1.legend(ncol=1, bbox_to_anchor=(0., 1.02, 1., 0.102), loc=3)
+ figure.savefig(path, bbox_inches="tight", pad_inches=0.05)
+
+def plot_results(args, history_x, history_u, history_g=None):
+ """
+ Args:
+ history_x (numpy.ndarray): history of state, shape(iters, state_size)
+ history_u (numpy.ndarray): history of state, shape(iters, input_size)
+ Returns:
+ """
+ plot_result(history_x, history_g=history_g, ylabel="x",
+ name="state_history",
+ save_dir="./result/" + args.controller_type)
+ plot_result(history_u, history_g=np.zeros_like(history_u), ylabel="u",
+ name="input_history",
+ save_dir="./result/" + args.controller_type)
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/runners/__init__.py b/PythonLinearNonlinearControl/runners/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/PythonLinearNonlinearControl/runners/make_runners.py b/PythonLinearNonlinearControl/runners/make_runners.py
new file mode 100644
index 0000000..be08186
--- /dev/null
+++ b/PythonLinearNonlinearControl/runners/make_runners.py
@@ -0,0 +1,4 @@
+from .runner import ExpRunner
+
+def make_runner(args):
+ return ExpRunner()
\ No newline at end of file
diff --git a/PythonLinearNonlinearControl/runners/runner.py b/PythonLinearNonlinearControl/runners/runner.py
new file mode 100644
index 0000000..0c55bb9
--- /dev/null
+++ b/PythonLinearNonlinearControl/runners/runner.py
@@ -0,0 +1,51 @@
+from logging import getLogger
+
+import numpy as np
+
+logger = getLogger(__name__)
+
+class ExpRunner():
+ """ experiment runner
+ """
+ def __init__(self):
+ """
+ """
+ pass
+
+ def run(self, env, controller, planner):
+ """
+ Returns:
+ history_x (numpy.ndarray): history of the state,
+ shape(episode length, state_size)
+ history_u (numpy.ndarray): history of the state,
+ shape(episode length, input_size)
+ """
+ done = False
+ curr_x, info = env.reset()
+ history_x, history_u, history_g = [], [], []
+ step_count = 0
+ score = 0.
+
+ while not done:
+ logger.debug("Step = {}".format(step_count))
+ # plan
+ g_xs = planner.plan(curr_x, g_x=info["goal_state"])
+
+ # obtain sol
+ u = controller.obtain_sol(curr_x, g_xs)
+
+ # step
+ next_x, cost, done, info = env.step(u)
+
+ # save
+ history_u.append(u)
+ history_x.append(curr_x)
+ history_g.append(g_xs[0])
+ # update
+ curr_x = next_x
+ score += cost
+ step_count += 1
+
+ logger.debug("Controller type = {}, Score = {}"\
+ .format(controller, score))
+ return np.array(history_x), np.array(history_u), np.array(history_g)
\ No newline at end of file
diff --git a/README.md b/README.md
index ade05e1..e4381d4 100644
--- a/README.md
+++ b/README.md
@@ -1,35 +1,148 @@
[](LICENSE)
-# linear_nonlinear_control
-Implementing the linear and nonlinear control theories.
-For an instance, model predictive control, nonlinear model predictive control, sliding mode control etc
+# PythonLinearNonLinearControl
-Now you can see the examples of control theories as following
+PythonLinearNonLinearControl is a library implementing the linear and nonlinear control theories in python.
-- **Iterative Linear Quadratic Regulator (iLQR)**
-- **Nonlinear Model Predictive Control (NMPC) with CGMRES**
-- **Nonlinear Model Predictive Control (NMPC) with Newton method**
-- **Linear Model Predictive Control (MPC)**(as generic function such as matlab tool box)
-- **Extended Linear Model Predictive Control for vehicle model**
+# Algorithms
-# Usage and Details
-you can see the usage in each folder
+| Algorithm | Use Linear Model | Use Nonlinear Model | Need Gradient (Hamiltonian) | Need Gradient (Model) |
+|:----------|:---------------:|:----------------:|:----------------:|
+| Linear Model Predictive Control (MPC) | ✓ | x | x | x |
+| Cross Entropy Method (CEM) | ✓ | ✓ | x | x |
+| Model Preidictive Path Integral Control (MPPI) | ✓ | ✓ | x | x |
+| Random Shooting Method (Random) | ✓ | ✓ | x | x |
+| Iterative LQR (iLQR) | ✓ | ✓ | x | ✓ |
+| Nonlinear Model Predictive Control -CGMRES- (NMPC-CGMRES) | ✓ | ✓ | ✓ | x |
+| Nonlinear Model Predictive Control -Newton- (NMPC-Newton) | ✓ | ✓ | x | x |
-# Basic Requirement
+"Need Gradient" means that you have to implement the gradient of the model or the gradient of hamiltonian.
+This library is also easily to extend for your own situations.
+
+Following algorithms are implemented in PythonLinearNonlinearControl
+
+- [Linear Model Predictive Control (MPC)](http://www2.eng.cam.ac.uk/~jmm1/mpcbook/mpcbook.html)
+ - Ref: Maciejowski, J. M. (2002). Predictive control: with constraints.
+ - [script]()
+- [Cross Entropy Method (CEM)](https://arxiv.org/abs/1805.12114)
+ - Ref: Chua, K., Calandra, R., McAllister, R., & Levine, S. (2018). Deep reinforcement learning in a handful of trials using probabilistic dynamics models. In Advances in Neural Information Processing Systems (pp. 4754-4765)
+ - [script]()
+- [Model Preidictive Path Integral Control (MPPI)](https://arxiv.org/abs/1909.11652)
+ - Ref: Nagabandi, A., Konoglie, K., Levine, S., & Kumar, V. (2019). Deep Dynamics Models for Learning Dexterous Manipulation. arXiv preprint arXiv:1909.11652.
+ - [script]()
+- [Random Shooting Method (Random)](https://arxiv.org/abs/1805.12114)
+ - Ref: Chua, K., Calandra, R., McAllister, R., & Levine, S. (2018). Deep reinforcement learning in a handful of trials using probabilistic dynamics models. In Advances in Neural Information Processing Systems (pp. 4754-4765)
+ - [script]()
+- [Iterative LQR (iLQR)](https://ieeexplore.ieee.org/document/6386025)
+ - Ref: Tassa, Y., Erez, T., & Todorov, E. (2012, October). Synthesis and stabilization of complex behaviors through online trajectory optimization. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (pp. 4906-4913). IEEE. and [Study Wolf](https://github.com/studywolf/control)
+ - [script]()
+- [Unconstrained Nonlinear Model Predictive Control](https://www.sciencedirect.com/science/article/pii/S0005109897000058)
+ - Ref: Ohtsuka, T., & Fujii, H. A. (1997). Real-time optimization algorithm for nonlinear receding-horizon control. Automatica, 33(6), 1147-1154.
+ - [script]()
+- [Constrained Nonlinear Model Predictive Control -CGMRES- (NMPC-CGMRES)](https://www.sciencedirect.com/science/article/pii/S0005109897000058)
+ - Ref: Ohtsuka, T., & Fujii, H. A. (1997). Real-time optimization algorithm for nonlinear receding-horizon control. Automatica, 33(6), 1147-1154.
+ - [script]()
+- [Constrained Nonlinear Model Predictive Control -Newton- (NMPC-Newton)](https://www.sciencedirect.com/science/article/pii/S0005109897000058)
+ - Ref: Ohtsuka, T., & Fujii, H. A. (1997). Real-time optimization algorithm for nonlinear receding-horizon control. Automatica, 33(6), 1147-1154.
+ - [script]()
+
+# Environments
+
+| Name | Linear | Nonlinear | State Size | Input size |
+|:----------|:---------------:|:----------------:|:----------------:|
+| First Order Lag System | ✓ | x | 4 | 2 |
+| Auto Cruse Control System | x | ✓ | 4 | 2 |
+| Two wheeled System | x | ✓ | 4 | 2 |
+
+All environments are continuous.
+**It should be noted that the algorithms for linear model could be applied to nonlinear enviroments if you have linealized the model of nonlinear environments.**
+
+# Usage
+
+## To install this package
+
+```
+python setup.py install
+```
+
+or
+
+```
+pip install .
+```
+
+## When developing the package
+
+```
+python setup.py develop
+```
+
+or
+
+```
+pip install -e .
+```
+
+## Run Experiments
+
+You can run the experiments as follows:
+
+```
+python scripts/simple_run.py --model "first-order_lag" --controller "CEM"
+```
+
+**figures and animations are saved in the ./result folder.**
+
+# Basic concepts
+
+When we design control systems, we should have **Model**, **Planner**, **Controller** and **Runner** as shown in the figure.
+It should be noted that **Model** and **Environment** are different. As mentioned before, we the algorithms for linear model could be applied to nonlinear enviroments if you have linealized model of nonlinear environments. In addition, you can use Neural Network or any non-linear functions to the model, although this library can not deal with it now.
+
+## Model
+
+System model. For an instance, in the case that a model is linear, this model should have a form, "x[k+1] = Ax[k] + Bu[k]".
+
+If you use gradient based control method, you are preferred to implement the gradients of the model, other wise the controllers use numeric gradients.
+
+## Planner
+
+Planner make the goal states.
+
+## Controller
+
+Controller calculate the optimal inputs by using the model by using the algorithms.
+
+## Runner
+
+Runner runs the simulation.
+
+Please, see more detail in each scripts.
+
+# Old version
+
+If you are interested in the old version of this library, that was not a library just examples, please see [v1.0](https://github.com/Shunichi09/PythonLinearNonlinearControl/tree/v1.0)
+
+# Documents
+
+Coming soon !!
+
+# Requirements
-- python3.5 or more
- numpy
- matplotlib
+- cvxopt
+- scipy
# License
-MIT
+
+[MIT License](LICENSE).
# Citation
```
-@Misc{pythonlinearnonlinearControl,
+@Misc{PythonLinearNonLinearControl,
author = {Shunichi Sekiguchi},
-title = {pythonlinearnonlinearControl},
-note = "\url{https://github.com/Shunichi09/linear_nonlinear_control}",
+title = {PythonLinearNonlinearControl},
+note = "\url{https://github.com/Shunichi09/PythonLinearNonlinearControl}",
}
```
diff --git a/ilqr/README.md b/ilqr/README.md
deleted file mode 100644
index 73a1c88..0000000
--- a/ilqr/README.md
+++ /dev/null
@@ -1,76 +0,0 @@
-# Iterative Linear Quadratic Regulator
-This program is about iLQR (Iteratice Linear Quadratic Regulator)
-
-# Problem Formulation
-
-Two wheeled robot is expressed by the following equation.
-It is nonlinear and nonholonomic system. Sometimes, it's extremely difficult to control the
-steering(or angular velocity) and velocity of the wheeled robot. Therefore, many methods control only steering, like purepersuit, Linear MPC.
-However, sometimes we should consider the velocity and steering simultaneously when the car or robots move fast.
-To solve the problem, we should apply the control methods which can treat the nonlinear system.
-
-&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}) -
-Nonliner Model Predictive Control is one of the famous methods, so I applied the method to two-wheeled robot which is included in the folder of this repository.
-(if you are interested, please go to nmpc/ folder of this repository)
-
-NMPC is very effecitive method to solve nonlinear optimal control problem but it is a handcraft method.
-This program is about one more other methods to solve the nonlinear optimal control problem.
-
-The method is iterative LQR.
-Iterative LQR is one of the DDP(differential dynamic programming) methods.
-Recently, this method is used in model-based RL(reinforcement learning).
-Although, this method cannot guarantee to obtain the global optimal answer, we could apply any model such as nonliner model or time-varing model even the model that expressed by NN.
-(Still we can only get approximate optimal anwser)
-
-If you want to know more about the iLQR, please look the references.
-The paper and website are great.
-
-# Usage
-
-## static goal
-
-```
-$ python3 main_static.py
-```
-
-## dynamic goal
-
-```
-$ python3 main_dynamic.py
-```
-
-# Expected Results
-
-- static goal
-
-
-
-Nonliner Model Predictive Control is one of the famous methods, so I applied the method to two-wheeled robot which is included in the folder of this repository.
-(if you are interested, please go to nmpc/ folder of this repository)
-
-NMPC is very effecitive method to solve nonlinear optimal control problem but it is a handcraft method.
-This program is about one more other methods to solve the nonlinear optimal control problem.
-
-The method is iterative LQR.
-Iterative LQR is one of the DDP(differential dynamic programming) methods.
-Recently, this method is used in model-based RL(reinforcement learning).
-Although, this method cannot guarantee to obtain the global optimal answer, we could apply any model such as nonliner model or time-varing model even the model that expressed by NN.
-(Still we can only get approximate optimal anwser)
-
-If you want to know more about the iLQR, please look the references.
-The paper and website are great.
-
-# Usage
-
-## static goal
-
-```
-$ python3 main_static.py
-```
-
-## dynamic goal
-
-```
-$ python3 main_dynamic.py
-```
-
-# Expected Results
-
-- static goal
-
- -
-
-
- -
-
-- track the goal
-
-
-
-
-
-- track the goal
-
-
- -
-
-
- -
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-
-- study wolf
-https://github.com/studywolf/control
-
-- Sergey Levine's lecture
-http://rail.eecs.berkeley.edu/deeprlcourse/
-
-- Tassa, Y., Erez, T., & Todorov, E. (2012). Synthesis and stabilization of complex behaviors through online trajectory optimization. IEEE International Conference on Intelligent Robots and Systems, 4906–4913. https://doi.org/10.1109/IROS.2012.6386025
-
-- Li, W., & Todorov, E. (n.d.). Iterative Linear Quadratic Regulator Design for Nonlinear Biological Movement Systems. Retrieved from https://homes.cs.washington.edu/~todorov/papers/LiICINCO04.pdf
diff --git a/ilqr/animation.py b/ilqr/animation.py
deleted file mode 100644
index ccb3b0d..0000000
--- a/ilqr/animation.py
+++ /dev/null
@@ -1,297 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.car_history_state = objects[0]
- self.target = objects[1]
-
- self.history_target_x = [self.target[:, 0]]
- self.history_target_y = [self.target[:, 1]]
-
- self.history_xs = [self.car_history_state[:, 0]]
- self.history_ys = [self.car_history_state[:, 1]]
- self.history_ths = [self.car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure()
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=10):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 2
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 2
- HIGH_MARGIN = 2
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], "*", color="b")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 1.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # goal
- self.traj_imgs[-1].set_data(self.history_target_x[0][i-1], self.history_target_y[0][i-1])
-
- # traj_ref
- self.traj_imgs[1].set_data(self.history_target_x[0][:i], self.history_target_y[0][:i])
\ No newline at end of file
diff --git a/ilqr/goal_maker.py b/ilqr/goal_maker.py
deleted file mode 100644
index 2112006..0000000
--- a/ilqr/goal_maker.py
+++ /dev/null
@@ -1,117 +0,0 @@
-import numpy as np
-import math
-import matplotlib.pyplot as plt
-
-def make_trajectory(goal_type, N):
- """
- Parameters
- -------------
- goal_type : str
- goal type
- N : int
- length of reference trajectory
- Returns
- -----------
- ref_trajectory : numpy.ndarray, shape(N, STATE_SIZE)
-
- Notes
- ---------
- this function can only deal with the
- """
-
- if goal_type == "const":
- ref_trajectory = np.array([[5., 3., 0.]])
-
- return ref_trajectory
-
- if goal_type == "sin":
- # parameters
- amplitude = 2.
- num_period = 2.
-
- ref_x_trajectory = np.linspace(0., 2 * math.pi * num_period, N)
- ref_y_trajectory = amplitude * np.sin(ref_x_trajectory)
-
- ref_xy_trajectory = np.stack((ref_x_trajectory, ref_y_trajectory))
-
- # target of theta is always zero
- ref_trajectory = np.vstack((ref_xy_trajectory, np.zeros((1, N))))
-
- return ref_trajectory.T
-
-class GoalMaker():
- """
- Attributes
- -----------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- ref_traj : numpy.ndarray, shape(N, STATE_SIZE)
- in this case the state size is 3
- """
-
- def __init__(self, N=500, goal_type="const", dt=0.01):
- """
- Parameters
- --------------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- """
- self.N = N
- self.goal_type = goal_type
- self.dt = dt
-
- self.ref_traj = None
- self.history_target = []
-
- def preprocess(self):
- """preprocess of make goal
- """
- goal_type_list = ["const", "sin"]
-
- if self.goal_type not in goal_type_list:
- raise KeyError("{0} is not in implemented goal type. please implement that!!".format(self.goal_type))
-
- self.ref_traj = make_trajectory(self.goal_type, self.N)
-
- def calc_goal(self, x):
- """ calclate nearest goal
- Parameters
- ------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- state of the system
-
- Returns
- ------------
- goal : numpy.ndarray, shape(STATE_SIZE, )
- """
-
- # search nearest point
- x_dis = (self.ref_traj[:, 0]-x[0])**2
- y_dis = (self.ref_traj[:, 1]-x[1])**2
- index = np.argmin(np.sqrt(x_dis + y_dis))
-
- print(index)
-
- MARGIN = 30
- if not self.goal_type == "const":
- index += MARGIN
-
- if index > self.N-1:
- index = self.N - 1
-
- goal = self.ref_traj[index]
-
- self.history_target.append(goal)
-
- return goal
-
-if __name__ == "__main__":
- make_trajectory("sin", 400)
\ No newline at end of file
diff --git a/ilqr/ilqr.py b/ilqr/ilqr.py
deleted file mode 100644
index 21a0c16..0000000
--- a/ilqr/ilqr.py
+++ /dev/null
@@ -1,463 +0,0 @@
-import numpy as np
-from copy import copy, deepcopy
-
-from model import TwoWheeledCar
-
-class iLQRController():
- """
- A controller that implements iterative Linear Quadratic control.
- Controls the (x, y, th) of the two wheeled car
-
- Attributes:
- ------------
- tN : int
- number of time step
- STATE_SIZE : int
- system state size
- INPUT_SIZE : int
- system input size
- dt : float
- sampling time
- max_iter : int
- number of max iteration
- lamb_factor : int
- lambda factor is that the adding value to make the matrix of Q _uu be positive
- lamb_max : float
- maximum lambda value to make the matrix of Q _uu be positive
- eps_converge : float
- threshold value of the iteration
- """
-
- def __init__(self, N=100, max_iter=400, dt=0.01):
- """
- Parameters
- ----------
- N : int, optional
- number of time step, default is 100
- max_iter : int, optional
- number of max iteration, default is 400
- dt : float, optional
- sampling time, default is 0.01
- """
- self.tN = N
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
- self.dt = dt
-
- self.max_iter = max_iter
- self.lamb_factor = 10
- self.lamb_max = 1e4
- self.eps_converge = 0.001
-
- def calc_input(self, car, x_target):
- """main loop of iterative LQR
-
- Parameters
- -------------
- car : model class
- should have initialize state and update state
- x_target : numpy.ndarray, shape(STATE_SIZE, )
- target state
-
- Returns
- -----------
- u : numpy.ndarray, shape(INPUT_SIZE, )
-
- See also
- ----------
- model.py
- """
-
- # initialize
- self.reset(x_target)
-
- # Compute the optimization
- x0 = np.zeros(self.STATE_SIZE)
- self.simulator, x0 = self.initialize_simulator(car)
- U = np.copy(self.U)
- self.X, self.U, cost = self.ilqr(x0, U)
-
- self.u = self.U[self.t] # use only one time step (like MPC)
-
- return self.u
-
- def initialize_simulator(self, car):
- """ make copy for controller
- Parameters
- -------------
- car : model class
- should have initialize state and update state
-
- Returns
- ----------
- simulator : model class
- should have initialize state and update state
- x0 : numpy.ndarray, shape(STATE_SIZE)
- initial state of the simulator
- """
- # copy
- simulator = TwoWheeledCar(deepcopy(car.xs))
-
- return simulator, deepcopy(simulator.xs)
-
- def cost(self, xs, us):
- """ the immediate state cost function
-
- Parameters
- ------------
- xs : shape(STATE_SIZE, tN + 1)
- predict state of the system
- us : shape(STATE_SIZE, tN)
- predict input of the system
-
- Returns
- ----------
- l : float
- stage cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- l_u : numpy.ndarray, shape(INPUT_SIZE, )
- differential of stage cost by u
- l_uu : numpy.ndarray, shape(INPUT_SIZE, INPUT_SIZE)
- second order differential of stage cost by uu
- l_ux numpy.ndarray, shape(INPUT_SIZE, STATE_SIZE)
- second order differential of stage cost by ux
- """
-
- # total cost
- R_11 = 1e-4 # terminal u_v cost weight
- R_22 = 1e-4 # terminal u_th cost weight
-
- l = np.dot(us.T, np.dot(np.diag([R_11, R_22]), us))
-
- # compute derivatives of cost
- l_x = np.zeros(self.STATE_SIZE)
- l_xx = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- l_u1 = 2. * us[0] * R_11
- l_u2 = 2. * us[1] * R_22
-
- l_u = np.array([l_u1, l_u2])
-
- l_uu = 2. * np.diag([R_11, R_22])
-
- l_ux = np.zeros((self.INPUT_SIZE, self.STATE_SIZE))
-
- return l, l_x, l_xx, l_u, l_uu, l_ux
-
- def cost_final(self, x):
- """ the final state cost function
-
- Parameters
- -------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- predict state of the system
-
- Returns
- ---------
- l : float
- terminal cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- """
- Q_11 = 10. # terminal x cost weight
- Q_22 = 10. # terminal y cost weight
- Q_33 = 0.1 # terminal theta cost weight
-
- error = self.simulator.xs - self.target
-
- l = np.dot(error.T, np.dot(np.diag([Q_11, Q_22, Q_33]), error))
-
- # about L_x
- l_x1 = 2. * (x[0] - self.target[0]) * Q_11
- l_x2 = 2. * (x[1] - self.target[1]) * Q_22
- l_x3 = 2. * (x[2] -self.target[2]) * Q_33
- l_x = np.array([l_x1, l_x2, l_x3])
-
- # about l_xx
- l_xx = 2. * np.diag([Q_11, Q_22, Q_33])
-
- # Final cost only requires these three values
- return l, l_x, l_xx
-
- def finite_differences(self, x, u):
- """ calculate gradient of plant dynamics using finite differences
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE,)
- the control input
-
- Returns
- ------------
- A : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- differential of the model /alpha X
- B : numpy.ndarray, shape(STATE_SIZE, INPUT_SIZE)
- differential of the model /alpha U
-
- Notes
- -------
- in this case, I pre-calculated the differential of the model because the tow-wheeled model is not difficult to calculate the gradient.
- If you dont or cannot do that, you can use the numerical differentiation.
- However, sometimes the the numerical differentiation affect the accuracy of calculations.
- """
-
- A = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
- A_ideal = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- B = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
- B_ideal = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- eps = 1e-4 # finite differences epsilon
-
- for ii in range(self.STATE_SIZE):
- # calculate partial differential w.r.t. x
- inc_x = x.copy()
- inc_x[ii] += eps
- state_inc,_ = self.plant_dynamics(inc_x, u.copy())
- dec_x = x.copy()
- dec_x[ii] -= eps
- state_dec,_ = self.plant_dynamics(dec_x, u.copy())
- A[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- A_ideal[0, 2] = -np.sin(x[2]) * u[0]
- A_ideal[1, 2] = np.cos(x[2]) * u[0]
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- for ii in range(self.INPUT_SIZE):
- # calculate partial differential w.r.t. u
- inc_u = u.copy()
- inc_u[ii] += eps
- state_inc,_ = self.plant_dynamics(x.copy(), inc_u)
- dec_u = u.copy()
- dec_u[ii] -= eps
- state_dec,_ = self.plant_dynamics(x.copy(), dec_u)
- B[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- B_ideal[0, 0] = np.cos(x[2])
- B_ideal[1, 0] = np.sin(x[2])
- B_ideal[2, 1] = 1.
-
- return A_ideal, B_ideal
-
- def ilqr(self, x0, U=None):
- """ use iterative linear quadratic regulation to find a control
- sequence that minimizes the cost function
-
- Parameters
- --------------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray(TIME, INPUT_SIZE)
- the initial control trajectory dimension
- """
- U = self.U if U is None else U
-
- lamb = 1.0 # regularization parameter
- sim_new_trajectory = True
- tN = U.shape[0] # number of time steps
-
- for ii in range(self.max_iter):
-
- if sim_new_trajectory == True:
- # simulate forward using the current control trajectory
- X, cost = self.simulate(x0, U)
- oldcost = np.copy(cost) # copy for exit condition check
-
- #
- f_x = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # df / dx
- f_u = np.zeros((tN, self.STATE_SIZE, self.INPUT_SIZE)) # df / du
- # for storing quadratized cost function
-
- l = np.zeros((tN,1)) # immediate state cost
- l_x = np.zeros((tN, self.STATE_SIZE)) # dl / dx
- l_xx = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # d^2 l / dx^2
- l_u = np.zeros((tN, self.INPUT_SIZE)) # dl / du
- l_uu = np.zeros((tN, self.INPUT_SIZE, self.INPUT_SIZE)) # d^2 l / du^2
- l_ux = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # d^2 l / du / dx
- # for everything except final state
- for t in range(tN-1):
- # x(t+1) = f(x(t), u(t)) = x(t) + dx(t) * dt
- # linearized dx(t) = np.dot(A(t), x(t)) + np.dot(B(t), u(t))
- # f_x = (np.eye + A(t)) * dt
- # f_u = (B(t)) * dt
- # continuous --> discrete
- A, B = self.finite_differences(X[t], U[t])
- f_x[t] = np.eye(self.STATE_SIZE) + A * self.dt
- f_u[t] = B * self.dt
-
- """ NOTE: why multiply dt in original program ??
- So the dt multiplication and + I is because we’re actually taking the derivative of the state with respect to the previous state. Which is not
- dx = Ax + Bu,
- but rather
- x(t) = x(t-1) + (Ax(t-1) + Bu(t-1))*dt
- And that’s where the identity matrix and dt come from!
- So that part’s in the comments of the code, but the *dt on all the cost function stuff is not commented on at all!
- So here the dt lets you normalize behaviour for different time steps (assuming you also scale the number of steps in the sequence).
- So if you have a time step of .01 or .001 you’re not racking up 10 times as much cost function in the latter case.
- And if you run the code with 50 steps in the sequence and dt=.01 and 500 steps in the sequence
- and dt=.001 you’ll see that you get the same results, which is not the case at all when you don’t take dt into account in the cost function!
- """
-
- (l[t], l_x[t], l_xx[t], l_u[t], l_uu[t], l_ux[t]) = self.cost(X[t], U[t])
-
- l[t] *= self.dt
- l_x[t] *= self.dt
- l_xx[t] *= self.dt
- l_u[t] *= self.dt
- l_uu[t] *= self.dt
- l_ux[t] *= self.dt
-
- # and for final state
- l[-1], l_x[-1], l_xx[-1] = self.cost_final(X[-1])
-
- sim_new_trajectory = False
-
- V = l[-1].copy() # value function
- V_x = l_x[-1].copy() # dV / dx
- V_xx = l_xx[-1].copy() # d^2 V / dx^2
- k = np.zeros((tN, self.INPUT_SIZE)) # feedforward modification
- K = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # feedback gain
-
- # work backwards to solve for V, Q, k, and K
- for t in range(self.tN-2, -1, -1):
- Q_x = l_x[t] + np.dot(f_x[t].T, V_x)
- Q_u = l_u[t] + np.dot(f_u[t].T, V_x)
-
- Q_xx = l_xx[t] + np.dot(f_x[t].T, np.dot(V_xx, f_x[t]))
- Q_ux = l_ux[t] + np.dot(f_u[t].T, np.dot(V_xx, f_x[t]))
- Q_uu = l_uu[t] + np.dot(f_u[t].T, np.dot(V_xx, f_u[t]))
-
- Q_uu_evals, Q_uu_evecs = np.linalg.eig(Q_uu)
- Q_uu_evals[Q_uu_evals < 0] = 0.0
- Q_uu_evals += lamb
- Q_uu_inv = np.dot(Q_uu_evecs, np.dot(np.diag(1.0/Q_uu_evals), Q_uu_evecs.T))
-
- k[t] = -1. * np.dot(Q_uu_inv, Q_u)
- K[t] = -1. * np.dot(Q_uu_inv, Q_ux)
-
- V_x = Q_x - np.dot(K[t].T, np.dot(Q_uu, k[t]))
- V_xx = Q_xx - np.dot(K[t].T, np.dot(Q_uu, K[t]))
-
- U_new = np.zeros((tN, self.INPUT_SIZE))
- x_new = x0.copy()
- for t in range(tN - 1):
- # use feedforward (k) and feedback (K) gain matrices
- # calculated from our value function approximation
- U_new[t] = U[t] + k[t] + np.dot(K[t], x_new - X[t])
- _,x_new = self.plant_dynamics(x_new, U_new[t])
-
- # evaluate the new trajectory
- X_new, cost_new = self.simulate(x0, U_new)
-
- if cost_new < cost:
- # decrease lambda (get closer to Newton's method)
- lamb /= self.lamb_factor
-
- X = np.copy(X_new) # update trajectory
- U = np.copy(U_new) # update control signal
- oldcost = np.copy(cost)
- cost = np.copy(cost_new)
-
- sim_new_trajectory = True # do another rollout
-
- # check to see if update is small enough to exit
- if ii > 0 and ((abs(oldcost-cost)/cost) < self.eps_converge):
- print("Converged at iteration = %d; Cost = %.4f;"%(ii,cost_new) +
- " logLambda = %.1f"%np.log(lamb))
- break
-
- else:
- # increase lambda (get closer to gradient descent)
- lamb *= self.lamb_factor
- # print("cost: %.4f, increasing lambda to %.4f")%(cost, lamb)
- if lamb > self.lamb_max:
- print("lambda > max_lambda at iteration = %d;"%ii +
- " Cost = %.4f; logLambda = %.1f"%(cost,
- np.log(lamb)))
- break
-
- return X, U, cost
-
- def plant_dynamics(self, x, u):
- """ simulate a single time step of the plant, from
- initial state x and applying control signal u
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE, )
- the control signal
-
- Returns
- -----------
- xdot : numpy.ndarray, shape(STATE_SIZE, )
- the gradient of x
- x_next : numpy.ndarray, shape(STATE_SIZE, )
- next state of x
- """
- self.simulator.initialize_state(x)
-
- # apply the control signal
- x_next = self.simulator.update_state(u, self.dt)
-
- # calculate the change in state
- xdot = ((x_next - x) / self.dt).squeeze()
-
- return xdot, x_next
-
- def reset(self, target):
- """ reset the state of the system """
-
- # Index along current control sequence
- self.t = 0
- self.U = np.zeros((self.tN, self.INPUT_SIZE))
- self.target = target.copy()
-
- def simulate(self, x0, U):
- """ do a rollout of the system, starting at x0 and
- applying the control sequence U
-
- Parameters
- ----------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray, shape(tN, INPUT_SIZE)
- the control sequence to apply
-
- Returns
- ---------
- X : numpy.ndarray, shape(tN, STATE_SIZE)
- the state sequence
- cost : float
- cost
- """
-
- tN = U.shape[0]
- X = np.zeros((tN, self.STATE_SIZE))
- X[0] = x0
- cost = 0
-
- # Run simulation with substeps
- for t in range(tN-1):
- _,X[t+1] = self.plant_dynamics(X[t], U[t])
- l, _ , _, _ , _ , _ = self.cost(X[t], U[t])
- cost = cost + self.dt * l
-
- # Adjust for final cost, subsample trajectory
- l_f, _, _ = self.cost_final(X[-1])
- cost = cost + l_f
-
- return X, cost
diff --git a/ilqr/main_dynamic.py b/ilqr/main_dynamic.py
deleted file mode 100644
index c6b22d6..0000000
--- a/ilqr/main_dynamic.py
+++ /dev/null
@@ -1,66 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="sin")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/main_static.py b/ilqr/main_static.py
deleted file mode 100644
index 3cceb82..0000000
--- a/ilqr/main_static.py
+++ /dev/null
@@ -1,68 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="const")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
-
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/model.py b/ilqr/model.py
deleted file mode 100644
index 4030c8f..0000000
--- a/ilqr/model.py
+++ /dev/null
@@ -1,131 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-
-"""
-このWheeled modelはコントローラー用
-ホントはbase作って、継承すべきですが省略
-"""
-class TwoWheeledCar():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
-
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt):
- """
- Palameters
- ------------
- us : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
- return self.xs.copy()
-
- def initialize_state(self, init_xs):
- """
- initialize the state
-
- Parameters
- ------------
- init_xs : numpy.ndarray
- """
- self.xs = init_xs.flatten()
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
\ No newline at end of file
diff --git a/mpc/basic/README.md b/mpc/basic/README.md
deleted file mode 100644
index 0d64664..0000000
--- a/mpc/basic/README.md
+++ /dev/null
@@ -1,146 +0,0 @@
-# Model Predictive Control Basic Tool
-This program is about template, generic function of linear model predictive control
-
-# Documentation of the MPC function
-Linear model predicitive control should have state equation.
-So if you want to use this function, you should model the plant as state equation.
-Therefore, the parameters of this class are as following
-
-**class MpcController()**
-
-Attributes :
-
-- A : numpy.ndarray
- - system matrix
-- B : numpy.ndarray
- - input matrix
-- Q : numpy.ndarray
- - evaluation function weight for states
-- Qs : numpy.ndarray
- - concatenated evaluation function weight for states
-- R : numpy.ndarray
- - evaluation function weight for inputs
-- Rs : numpy.ndarray
- - concatenated evaluation function weight for inputs
-- pre_step : int
- - prediction step
-- state_size : int
- - state size of the plant
-- input_size : int
- - input size of the plant
-- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-- input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-
-Methods:
-
-- initialize_controller() initialize the controller
-- calc_input(states, references) calculating optimal input
-
-More details, please look the **mpc_func_with_scipy.py** and **mpc_func_with_cvxopt.py**
-
-We have two function, mpc_func_with_cvxopt.py and mpc_func_with_scipy.py
-Both functions have same variable and member function. However the solver is different.
-Plese choose the right method for your environment.
-
-- example of import
-
-```py
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-```
-
-# Examples
-## Problem Formulation
-
-- **first order system**
-
-
-
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-
-- study wolf
-https://github.com/studywolf/control
-
-- Sergey Levine's lecture
-http://rail.eecs.berkeley.edu/deeprlcourse/
-
-- Tassa, Y., Erez, T., & Todorov, E. (2012). Synthesis and stabilization of complex behaviors through online trajectory optimization. IEEE International Conference on Intelligent Robots and Systems, 4906–4913. https://doi.org/10.1109/IROS.2012.6386025
-
-- Li, W., & Todorov, E. (n.d.). Iterative Linear Quadratic Regulator Design for Nonlinear Biological Movement Systems. Retrieved from https://homes.cs.washington.edu/~todorov/papers/LiICINCO04.pdf
diff --git a/ilqr/animation.py b/ilqr/animation.py
deleted file mode 100644
index ccb3b0d..0000000
--- a/ilqr/animation.py
+++ /dev/null
@@ -1,297 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.car_history_state = objects[0]
- self.target = objects[1]
-
- self.history_target_x = [self.target[:, 0]]
- self.history_target_y = [self.target[:, 1]]
-
- self.history_xs = [self.car_history_state[:, 0]]
- self.history_ys = [self.car_history_state[:, 1]]
- self.history_ths = [self.car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure()
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=10):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 2
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 2
- HIGH_MARGIN = 2
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], "*", color="b")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 1.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # goal
- self.traj_imgs[-1].set_data(self.history_target_x[0][i-1], self.history_target_y[0][i-1])
-
- # traj_ref
- self.traj_imgs[1].set_data(self.history_target_x[0][:i], self.history_target_y[0][:i])
\ No newline at end of file
diff --git a/ilqr/goal_maker.py b/ilqr/goal_maker.py
deleted file mode 100644
index 2112006..0000000
--- a/ilqr/goal_maker.py
+++ /dev/null
@@ -1,117 +0,0 @@
-import numpy as np
-import math
-import matplotlib.pyplot as plt
-
-def make_trajectory(goal_type, N):
- """
- Parameters
- -------------
- goal_type : str
- goal type
- N : int
- length of reference trajectory
- Returns
- -----------
- ref_trajectory : numpy.ndarray, shape(N, STATE_SIZE)
-
- Notes
- ---------
- this function can only deal with the
- """
-
- if goal_type == "const":
- ref_trajectory = np.array([[5., 3., 0.]])
-
- return ref_trajectory
-
- if goal_type == "sin":
- # parameters
- amplitude = 2.
- num_period = 2.
-
- ref_x_trajectory = np.linspace(0., 2 * math.pi * num_period, N)
- ref_y_trajectory = amplitude * np.sin(ref_x_trajectory)
-
- ref_xy_trajectory = np.stack((ref_x_trajectory, ref_y_trajectory))
-
- # target of theta is always zero
- ref_trajectory = np.vstack((ref_xy_trajectory, np.zeros((1, N))))
-
- return ref_trajectory.T
-
-class GoalMaker():
- """
- Attributes
- -----------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- ref_traj : numpy.ndarray, shape(N, STATE_SIZE)
- in this case the state size is 3
- """
-
- def __init__(self, N=500, goal_type="const", dt=0.01):
- """
- Parameters
- --------------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- """
- self.N = N
- self.goal_type = goal_type
- self.dt = dt
-
- self.ref_traj = None
- self.history_target = []
-
- def preprocess(self):
- """preprocess of make goal
- """
- goal_type_list = ["const", "sin"]
-
- if self.goal_type not in goal_type_list:
- raise KeyError("{0} is not in implemented goal type. please implement that!!".format(self.goal_type))
-
- self.ref_traj = make_trajectory(self.goal_type, self.N)
-
- def calc_goal(self, x):
- """ calclate nearest goal
- Parameters
- ------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- state of the system
-
- Returns
- ------------
- goal : numpy.ndarray, shape(STATE_SIZE, )
- """
-
- # search nearest point
- x_dis = (self.ref_traj[:, 0]-x[0])**2
- y_dis = (self.ref_traj[:, 1]-x[1])**2
- index = np.argmin(np.sqrt(x_dis + y_dis))
-
- print(index)
-
- MARGIN = 30
- if not self.goal_type == "const":
- index += MARGIN
-
- if index > self.N-1:
- index = self.N - 1
-
- goal = self.ref_traj[index]
-
- self.history_target.append(goal)
-
- return goal
-
-if __name__ == "__main__":
- make_trajectory("sin", 400)
\ No newline at end of file
diff --git a/ilqr/ilqr.py b/ilqr/ilqr.py
deleted file mode 100644
index 21a0c16..0000000
--- a/ilqr/ilqr.py
+++ /dev/null
@@ -1,463 +0,0 @@
-import numpy as np
-from copy import copy, deepcopy
-
-from model import TwoWheeledCar
-
-class iLQRController():
- """
- A controller that implements iterative Linear Quadratic control.
- Controls the (x, y, th) of the two wheeled car
-
- Attributes:
- ------------
- tN : int
- number of time step
- STATE_SIZE : int
- system state size
- INPUT_SIZE : int
- system input size
- dt : float
- sampling time
- max_iter : int
- number of max iteration
- lamb_factor : int
- lambda factor is that the adding value to make the matrix of Q _uu be positive
- lamb_max : float
- maximum lambda value to make the matrix of Q _uu be positive
- eps_converge : float
- threshold value of the iteration
- """
-
- def __init__(self, N=100, max_iter=400, dt=0.01):
- """
- Parameters
- ----------
- N : int, optional
- number of time step, default is 100
- max_iter : int, optional
- number of max iteration, default is 400
- dt : float, optional
- sampling time, default is 0.01
- """
- self.tN = N
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
- self.dt = dt
-
- self.max_iter = max_iter
- self.lamb_factor = 10
- self.lamb_max = 1e4
- self.eps_converge = 0.001
-
- def calc_input(self, car, x_target):
- """main loop of iterative LQR
-
- Parameters
- -------------
- car : model class
- should have initialize state and update state
- x_target : numpy.ndarray, shape(STATE_SIZE, )
- target state
-
- Returns
- -----------
- u : numpy.ndarray, shape(INPUT_SIZE, )
-
- See also
- ----------
- model.py
- """
-
- # initialize
- self.reset(x_target)
-
- # Compute the optimization
- x0 = np.zeros(self.STATE_SIZE)
- self.simulator, x0 = self.initialize_simulator(car)
- U = np.copy(self.U)
- self.X, self.U, cost = self.ilqr(x0, U)
-
- self.u = self.U[self.t] # use only one time step (like MPC)
-
- return self.u
-
- def initialize_simulator(self, car):
- """ make copy for controller
- Parameters
- -------------
- car : model class
- should have initialize state and update state
-
- Returns
- ----------
- simulator : model class
- should have initialize state and update state
- x0 : numpy.ndarray, shape(STATE_SIZE)
- initial state of the simulator
- """
- # copy
- simulator = TwoWheeledCar(deepcopy(car.xs))
-
- return simulator, deepcopy(simulator.xs)
-
- def cost(self, xs, us):
- """ the immediate state cost function
-
- Parameters
- ------------
- xs : shape(STATE_SIZE, tN + 1)
- predict state of the system
- us : shape(STATE_SIZE, tN)
- predict input of the system
-
- Returns
- ----------
- l : float
- stage cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- l_u : numpy.ndarray, shape(INPUT_SIZE, )
- differential of stage cost by u
- l_uu : numpy.ndarray, shape(INPUT_SIZE, INPUT_SIZE)
- second order differential of stage cost by uu
- l_ux numpy.ndarray, shape(INPUT_SIZE, STATE_SIZE)
- second order differential of stage cost by ux
- """
-
- # total cost
- R_11 = 1e-4 # terminal u_v cost weight
- R_22 = 1e-4 # terminal u_th cost weight
-
- l = np.dot(us.T, np.dot(np.diag([R_11, R_22]), us))
-
- # compute derivatives of cost
- l_x = np.zeros(self.STATE_SIZE)
- l_xx = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- l_u1 = 2. * us[0] * R_11
- l_u2 = 2. * us[1] * R_22
-
- l_u = np.array([l_u1, l_u2])
-
- l_uu = 2. * np.diag([R_11, R_22])
-
- l_ux = np.zeros((self.INPUT_SIZE, self.STATE_SIZE))
-
- return l, l_x, l_xx, l_u, l_uu, l_ux
-
- def cost_final(self, x):
- """ the final state cost function
-
- Parameters
- -------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- predict state of the system
-
- Returns
- ---------
- l : float
- terminal cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- """
- Q_11 = 10. # terminal x cost weight
- Q_22 = 10. # terminal y cost weight
- Q_33 = 0.1 # terminal theta cost weight
-
- error = self.simulator.xs - self.target
-
- l = np.dot(error.T, np.dot(np.diag([Q_11, Q_22, Q_33]), error))
-
- # about L_x
- l_x1 = 2. * (x[0] - self.target[0]) * Q_11
- l_x2 = 2. * (x[1] - self.target[1]) * Q_22
- l_x3 = 2. * (x[2] -self.target[2]) * Q_33
- l_x = np.array([l_x1, l_x2, l_x3])
-
- # about l_xx
- l_xx = 2. * np.diag([Q_11, Q_22, Q_33])
-
- # Final cost only requires these three values
- return l, l_x, l_xx
-
- def finite_differences(self, x, u):
- """ calculate gradient of plant dynamics using finite differences
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE,)
- the control input
-
- Returns
- ------------
- A : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- differential of the model /alpha X
- B : numpy.ndarray, shape(STATE_SIZE, INPUT_SIZE)
- differential of the model /alpha U
-
- Notes
- -------
- in this case, I pre-calculated the differential of the model because the tow-wheeled model is not difficult to calculate the gradient.
- If you dont or cannot do that, you can use the numerical differentiation.
- However, sometimes the the numerical differentiation affect the accuracy of calculations.
- """
-
- A = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
- A_ideal = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- B = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
- B_ideal = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- eps = 1e-4 # finite differences epsilon
-
- for ii in range(self.STATE_SIZE):
- # calculate partial differential w.r.t. x
- inc_x = x.copy()
- inc_x[ii] += eps
- state_inc,_ = self.plant_dynamics(inc_x, u.copy())
- dec_x = x.copy()
- dec_x[ii] -= eps
- state_dec,_ = self.plant_dynamics(dec_x, u.copy())
- A[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- A_ideal[0, 2] = -np.sin(x[2]) * u[0]
- A_ideal[1, 2] = np.cos(x[2]) * u[0]
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- for ii in range(self.INPUT_SIZE):
- # calculate partial differential w.r.t. u
- inc_u = u.copy()
- inc_u[ii] += eps
- state_inc,_ = self.plant_dynamics(x.copy(), inc_u)
- dec_u = u.copy()
- dec_u[ii] -= eps
- state_dec,_ = self.plant_dynamics(x.copy(), dec_u)
- B[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- B_ideal[0, 0] = np.cos(x[2])
- B_ideal[1, 0] = np.sin(x[2])
- B_ideal[2, 1] = 1.
-
- return A_ideal, B_ideal
-
- def ilqr(self, x0, U=None):
- """ use iterative linear quadratic regulation to find a control
- sequence that minimizes the cost function
-
- Parameters
- --------------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray(TIME, INPUT_SIZE)
- the initial control trajectory dimension
- """
- U = self.U if U is None else U
-
- lamb = 1.0 # regularization parameter
- sim_new_trajectory = True
- tN = U.shape[0] # number of time steps
-
- for ii in range(self.max_iter):
-
- if sim_new_trajectory == True:
- # simulate forward using the current control trajectory
- X, cost = self.simulate(x0, U)
- oldcost = np.copy(cost) # copy for exit condition check
-
- #
- f_x = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # df / dx
- f_u = np.zeros((tN, self.STATE_SIZE, self.INPUT_SIZE)) # df / du
- # for storing quadratized cost function
-
- l = np.zeros((tN,1)) # immediate state cost
- l_x = np.zeros((tN, self.STATE_SIZE)) # dl / dx
- l_xx = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # d^2 l / dx^2
- l_u = np.zeros((tN, self.INPUT_SIZE)) # dl / du
- l_uu = np.zeros((tN, self.INPUT_SIZE, self.INPUT_SIZE)) # d^2 l / du^2
- l_ux = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # d^2 l / du / dx
- # for everything except final state
- for t in range(tN-1):
- # x(t+1) = f(x(t), u(t)) = x(t) + dx(t) * dt
- # linearized dx(t) = np.dot(A(t), x(t)) + np.dot(B(t), u(t))
- # f_x = (np.eye + A(t)) * dt
- # f_u = (B(t)) * dt
- # continuous --> discrete
- A, B = self.finite_differences(X[t], U[t])
- f_x[t] = np.eye(self.STATE_SIZE) + A * self.dt
- f_u[t] = B * self.dt
-
- """ NOTE: why multiply dt in original program ??
- So the dt multiplication and + I is because we’re actually taking the derivative of the state with respect to the previous state. Which is not
- dx = Ax + Bu,
- but rather
- x(t) = x(t-1) + (Ax(t-1) + Bu(t-1))*dt
- And that’s where the identity matrix and dt come from!
- So that part’s in the comments of the code, but the *dt on all the cost function stuff is not commented on at all!
- So here the dt lets you normalize behaviour for different time steps (assuming you also scale the number of steps in the sequence).
- So if you have a time step of .01 or .001 you’re not racking up 10 times as much cost function in the latter case.
- And if you run the code with 50 steps in the sequence and dt=.01 and 500 steps in the sequence
- and dt=.001 you’ll see that you get the same results, which is not the case at all when you don’t take dt into account in the cost function!
- """
-
- (l[t], l_x[t], l_xx[t], l_u[t], l_uu[t], l_ux[t]) = self.cost(X[t], U[t])
-
- l[t] *= self.dt
- l_x[t] *= self.dt
- l_xx[t] *= self.dt
- l_u[t] *= self.dt
- l_uu[t] *= self.dt
- l_ux[t] *= self.dt
-
- # and for final state
- l[-1], l_x[-1], l_xx[-1] = self.cost_final(X[-1])
-
- sim_new_trajectory = False
-
- V = l[-1].copy() # value function
- V_x = l_x[-1].copy() # dV / dx
- V_xx = l_xx[-1].copy() # d^2 V / dx^2
- k = np.zeros((tN, self.INPUT_SIZE)) # feedforward modification
- K = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # feedback gain
-
- # work backwards to solve for V, Q, k, and K
- for t in range(self.tN-2, -1, -1):
- Q_x = l_x[t] + np.dot(f_x[t].T, V_x)
- Q_u = l_u[t] + np.dot(f_u[t].T, V_x)
-
- Q_xx = l_xx[t] + np.dot(f_x[t].T, np.dot(V_xx, f_x[t]))
- Q_ux = l_ux[t] + np.dot(f_u[t].T, np.dot(V_xx, f_x[t]))
- Q_uu = l_uu[t] + np.dot(f_u[t].T, np.dot(V_xx, f_u[t]))
-
- Q_uu_evals, Q_uu_evecs = np.linalg.eig(Q_uu)
- Q_uu_evals[Q_uu_evals < 0] = 0.0
- Q_uu_evals += lamb
- Q_uu_inv = np.dot(Q_uu_evecs, np.dot(np.diag(1.0/Q_uu_evals), Q_uu_evecs.T))
-
- k[t] = -1. * np.dot(Q_uu_inv, Q_u)
- K[t] = -1. * np.dot(Q_uu_inv, Q_ux)
-
- V_x = Q_x - np.dot(K[t].T, np.dot(Q_uu, k[t]))
- V_xx = Q_xx - np.dot(K[t].T, np.dot(Q_uu, K[t]))
-
- U_new = np.zeros((tN, self.INPUT_SIZE))
- x_new = x0.copy()
- for t in range(tN - 1):
- # use feedforward (k) and feedback (K) gain matrices
- # calculated from our value function approximation
- U_new[t] = U[t] + k[t] + np.dot(K[t], x_new - X[t])
- _,x_new = self.plant_dynamics(x_new, U_new[t])
-
- # evaluate the new trajectory
- X_new, cost_new = self.simulate(x0, U_new)
-
- if cost_new < cost:
- # decrease lambda (get closer to Newton's method)
- lamb /= self.lamb_factor
-
- X = np.copy(X_new) # update trajectory
- U = np.copy(U_new) # update control signal
- oldcost = np.copy(cost)
- cost = np.copy(cost_new)
-
- sim_new_trajectory = True # do another rollout
-
- # check to see if update is small enough to exit
- if ii > 0 and ((abs(oldcost-cost)/cost) < self.eps_converge):
- print("Converged at iteration = %d; Cost = %.4f;"%(ii,cost_new) +
- " logLambda = %.1f"%np.log(lamb))
- break
-
- else:
- # increase lambda (get closer to gradient descent)
- lamb *= self.lamb_factor
- # print("cost: %.4f, increasing lambda to %.4f")%(cost, lamb)
- if lamb > self.lamb_max:
- print("lambda > max_lambda at iteration = %d;"%ii +
- " Cost = %.4f; logLambda = %.1f"%(cost,
- np.log(lamb)))
- break
-
- return X, U, cost
-
- def plant_dynamics(self, x, u):
- """ simulate a single time step of the plant, from
- initial state x and applying control signal u
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE, )
- the control signal
-
- Returns
- -----------
- xdot : numpy.ndarray, shape(STATE_SIZE, )
- the gradient of x
- x_next : numpy.ndarray, shape(STATE_SIZE, )
- next state of x
- """
- self.simulator.initialize_state(x)
-
- # apply the control signal
- x_next = self.simulator.update_state(u, self.dt)
-
- # calculate the change in state
- xdot = ((x_next - x) / self.dt).squeeze()
-
- return xdot, x_next
-
- def reset(self, target):
- """ reset the state of the system """
-
- # Index along current control sequence
- self.t = 0
- self.U = np.zeros((self.tN, self.INPUT_SIZE))
- self.target = target.copy()
-
- def simulate(self, x0, U):
- """ do a rollout of the system, starting at x0 and
- applying the control sequence U
-
- Parameters
- ----------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray, shape(tN, INPUT_SIZE)
- the control sequence to apply
-
- Returns
- ---------
- X : numpy.ndarray, shape(tN, STATE_SIZE)
- the state sequence
- cost : float
- cost
- """
-
- tN = U.shape[0]
- X = np.zeros((tN, self.STATE_SIZE))
- X[0] = x0
- cost = 0
-
- # Run simulation with substeps
- for t in range(tN-1):
- _,X[t+1] = self.plant_dynamics(X[t], U[t])
- l, _ , _, _ , _ , _ = self.cost(X[t], U[t])
- cost = cost + self.dt * l
-
- # Adjust for final cost, subsample trajectory
- l_f, _, _ = self.cost_final(X[-1])
- cost = cost + l_f
-
- return X, cost
diff --git a/ilqr/main_dynamic.py b/ilqr/main_dynamic.py
deleted file mode 100644
index c6b22d6..0000000
--- a/ilqr/main_dynamic.py
+++ /dev/null
@@ -1,66 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="sin")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/main_static.py b/ilqr/main_static.py
deleted file mode 100644
index 3cceb82..0000000
--- a/ilqr/main_static.py
+++ /dev/null
@@ -1,68 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="const")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
-
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/model.py b/ilqr/model.py
deleted file mode 100644
index 4030c8f..0000000
--- a/ilqr/model.py
+++ /dev/null
@@ -1,131 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-
-"""
-このWheeled modelはコントローラー用
-ホントはbase作って、継承すべきですが省略
-"""
-class TwoWheeledCar():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
-
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt):
- """
- Palameters
- ------------
- us : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
- return self.xs.copy()
-
- def initialize_state(self, init_xs):
- """
- initialize the state
-
- Parameters
- ------------
- init_xs : numpy.ndarray
- """
- self.xs = init_xs.flatten()
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
\ No newline at end of file
diff --git a/mpc/basic/README.md b/mpc/basic/README.md
deleted file mode 100644
index 0d64664..0000000
--- a/mpc/basic/README.md
+++ /dev/null
@@ -1,146 +0,0 @@
-# Model Predictive Control Basic Tool
-This program is about template, generic function of linear model predictive control
-
-# Documentation of the MPC function
-Linear model predicitive control should have state equation.
-So if you want to use this function, you should model the plant as state equation.
-Therefore, the parameters of this class are as following
-
-**class MpcController()**
-
-Attributes :
-
-- A : numpy.ndarray
- - system matrix
-- B : numpy.ndarray
- - input matrix
-- Q : numpy.ndarray
- - evaluation function weight for states
-- Qs : numpy.ndarray
- - concatenated evaluation function weight for states
-- R : numpy.ndarray
- - evaluation function weight for inputs
-- Rs : numpy.ndarray
- - concatenated evaluation function weight for inputs
-- pre_step : int
- - prediction step
-- state_size : int
- - state size of the plant
-- input_size : int
- - input size of the plant
-- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-- input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-
-Methods:
-
-- initialize_controller() initialize the controller
-- calc_input(states, references) calculating optimal input
-
-More details, please look the **mpc_func_with_scipy.py** and **mpc_func_with_cvxopt.py**
-
-We have two function, mpc_func_with_cvxopt.py and mpc_func_with_scipy.py
-Both functions have same variable and member function. However the solver is different.
-Plese choose the right method for your environment.
-
-- example of import
-
-```py
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-```
-
-# Examples
-## Problem Formulation
-
-- **first order system**
-
- -
-- **ACC (Adaptive cruise control)**
-
-The two wheeled model are expressed the following equation.
-
-
-
-- **ACC (Adaptive cruise control)**
-
-The two wheeled model are expressed the following equation.
-
-&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}) -
-However, if we assume the velocity are constant, we can approximate the equation as following,
-
-
-
-However, if we assume the velocity are constant, we can approximate the equation as following,
-
- -
-then we can apply this model to linear mpc, we should give the model reference V although.
-
-- **evaluation function**
-
-the both examples have same evaluation function form as following equation.
-
-
-
-then we can apply this model to linear mpc, we should give the model reference V although.
-
-- **evaluation function**
-
-the both examples have same evaluation function form as following equation.
-
--\boldsymbol{r}(k+i|k)&space;||^2_{{\boldsymbol{Q}}(i)}&space;+&space;||\boldsymbol{\Delta&space;{U}}(k+i|k)||^2_{{\boldsymbol{R}}(i)}) -
--
-
--  is predicit state by using predict input
-
--
is predicit state by using predict input
-
--  is reference state
-
--
is reference state
-
--  is predict amount of change of input
-
--
is predict amount of change of input
-
--  are evaluation function weights
-
-## Expected Results
-
-- first order system
-
-- time history
-
-
are evaluation function weights
-
-## Expected Results
-
-- first order system
-
-- time history
-
- -
-- input
-
-
-
-- input
-
- -
-- ACC (Adaptive cruise control)
-
-- time history of states
-
-
-
-- ACC (Adaptive cruise control)
-
-- time history of states
-
- -
-- animation
-
-
-
-- animation
-
- -
-
-# Usage
-
-- for example(first order system)
-
-```
-$ python main_example.py
-```
-
-- for example(ACC (Adaptive cruise control))
-
-```
-$ python main_ACC.py
-```
-
-- for comparing two methods of optimization solvers
-
-```
-$ python test_compare_methods.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-- cvxopt
-- scipy1.2.0 or more
-- python-control
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- モデル予測制御―制約のもとでの最適制御 著:Jan M. Maciejowski 訳:足立修一 東京電機大学出版局
\ No newline at end of file
diff --git a/mpc/basic/animation.py b/mpc/basic/animation.py
deleted file mode 100755
index 6ece541..0000000
--- a/mpc/basic/animation.py
+++ /dev/null
@@ -1,233 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
- """
- self.lead_car_history_state = objects[0]
- self.follow_car_history_state = objects[1]
-
- self.history_xs = [self.lead_car_history_state[:, 0], self.follow_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1], self.follow_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2], self.follow_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.object_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- # (2) set the xlim and ylim
- self.axis.set_xlim(-5, 50)
- self.axis.set_ylim(-2, 5)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.object_imgs.append(temp_img)
-
- traj_color_list = ["k", "m"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- self._draw_objects(i)
- self._draw_traj(i)
-
- return self.object_imgs, self.traj_imgs,
-
- def _draw_objects(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- for j in range(2):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[j][i],
- self.history_ys[j][i],
- 1.0,
- self.history_ths[j][i])
-
- self.object_imgs[fix_j].set_data([object_x, object_y])
- self.object_imgs[fix_j + 1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- for j in range(2):
- self.traj_imgs[j].set_data(self.history_xs[j][:i], self.history_ys[j][:i])
\ No newline at end of file
diff --git a/mpc/basic/main_ACC.py b/mpc/basic/main_ACC.py
deleted file mode 100644
index a868559..0000000
--- a/mpc/basic/main_ACC.py
+++ /dev/null
@@ -1,246 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- A = np.array([[0., V], [0., 0.]])
- B = np.array([[0.], [1.]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_ACC_TEMP.py b/mpc/basic/main_ACC_TEMP.py
deleted file mode 100644
index 9ad7c97..0000000
--- a/mpc/basic/main_ACC_TEMP.py
+++ /dev/null
@@ -1,243 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-# from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- Ad = np.array([[1., V * dt], [0., 1.]])
- Bd = np.array([[0.], [1. * dt]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- # sysc = matlab.ss(A, B, C, D)
- # discrete system
- # sysd = matlab.c2d(sysc, dt)
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_example.py b/mpc/basic/main_example.py
deleted file mode 100644
index b768a21..0000000
--- a/mpc/basic/main_example.py
+++ /dev/null
@@ -1,188 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_xs : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- D : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
- # print("xs = {0}".format(self.xs))
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
-def main():
- dt = 0.05
- simulation_time = 30 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- print(Ad)
- print(Bd)
- input()
-
- # evaluation function weight
- Q = np.diag([1., 1., 1., 1.])
- R = np.diag([1., 1.])
- pre_step = 10
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
- states = plant.xs
- opt_u = controller.calc_input(states, reference)
- plant.update_state(opt_u, dt=dt)
-
- history_states = np.array(plant.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 0])
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 1])
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 2])
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 3])
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us = np.array(controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 0])
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 1])
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_cvxopt.py b/mpc/basic/mpc_func_with_cvxopt.py
deleted file mode 100644
index 4e04736..0000000
--- a/mpc/basic/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,256 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_scipy.py b/mpc/basic/mpc_func_with_scipy.py
deleted file mode 100644
index 54ef3c9..0000000
--- a/mpc/basic/mpc_func_with_scipy.py
+++ /dev/null
@@ -1,262 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from scipy.optimize import minimize
-from scipy.optimize import LinearConstraint
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error) )
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- def optimized_func(dt_us):
- """
- """
- temp_dt_us = np.array([dt_us[i] for i in range(self.input_size * self.pre_step)])
-
- return (np.dot(temp_dt_us, np.dot(H, temp_dt_us.reshape(-1, 1))) - np.dot(G.T, temp_dt_us.reshape(-1, 1)))[0]
-
- # constraint
- lb = np.array([-np.inf for _ in range(len(ub))])
- linear_cons = LinearConstraint(A, lb, ub)
-
- init_dt_us = np.zeros(self.input_size * self.pre_step)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = minimize(optimized_func, init_dt_us, constraints=[linear_cons])
-
- opt_dt_us = opt_result.x
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/test_compare_methods.py b/mpc/basic/test_compare_methods.py
deleted file mode 100644
index 5ddaea4..0000000
--- a/mpc/basic/test_compare_methods.py
+++ /dev/null
@@ -1,211 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- states : float
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_state : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- C : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
-
- # print("xs = {0}".format(self.xs))
- # a = input()
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.history_xs)
-
-def main():
- dt = 0.05
- simulation_time = 50 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant_cvxopt = FirstOrderSystem(A, B, C, init_states=init_xs)
- plant_scipy = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1., 10., 10.])
- R = np.diag([0.01, 0.01])
- pre_step = 5
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller_cvxopt = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_scipy = MpcController_scipy(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_cvxopt.initialize_controller()
- controller_scipy.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
-
- states_cvxopt = plant_cvxopt.xs
- states_scipy = plant_scipy.xs
-
- opt_u_cvxopt = controller_cvxopt.calc_input(states_cvxopt, reference)
- opt_u_scipy = controller_scipy.calc_input(states_scipy, reference)
-
- plant_cvxopt.update_state(opt_u_cvxopt)
- plant_scipy.update_state(opt_u_scipy)
-
- history_states_cvxopt = np.array(plant_cvxopt.history_xs)
- history_states_scipy = np.array(plant_scipy.history_xs)
-
- time_history_fig = plt.figure(dpi=75)
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 0], label="cvxopt")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 0], label="scipy", linestyle="dashdot")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
- v_x_fig.legend()
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 1], label="cvxopt")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 1], label="scipy", linestyle="dashdot")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
- v_y_fig.legend()
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 2], label="cvxopt")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 2], label="scipy", linestyle="dashdot")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 3], label ="cvxopt")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 3], label="scipy", linestyle="dashdot")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us_cvxopt = np.array(controller_cvxopt.history_us)
- history_us_scipy = np.array(controller_scipy.history_us)
-
- input_history_fig = plt.figure(dpi=75)
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 0], label="cvxopt")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 0], label="scipy", linestyle="dashdot")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
- u_1_fig.legend()
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 1], label="cvxopt")
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 1], label="scipy", linestyle="dashdot")
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- u_2_fig.legend()
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/README.md b/mpc/extend/README.md
deleted file mode 100644
index e926aa5..0000000
--- a/mpc/extend/README.md
+++ /dev/null
@@ -1,41 +0,0 @@
-# Model Predictive Control for Vehicle model
-This program is for controlling the vehicle model.
-I implemented the steering control for vehicle by using Model Predictive Control.
-
-# Model
-Usually, the vehicle model is expressed by extremely complicated nonlinear equation.
-Acoording to reference 1, I used the simple model as shown in following equation.
-
-
-
-
-# Usage
-
-- for example(first order system)
-
-```
-$ python main_example.py
-```
-
-- for example(ACC (Adaptive cruise control))
-
-```
-$ python main_ACC.py
-```
-
-- for comparing two methods of optimization solvers
-
-```
-$ python test_compare_methods.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-- cvxopt
-- scipy1.2.0 or more
-- python-control
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- モデル予測制御―制約のもとでの最適制御 著:Jan M. Maciejowski 訳:足立修一 東京電機大学出版局
\ No newline at end of file
diff --git a/mpc/basic/animation.py b/mpc/basic/animation.py
deleted file mode 100755
index 6ece541..0000000
--- a/mpc/basic/animation.py
+++ /dev/null
@@ -1,233 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
- """
- self.lead_car_history_state = objects[0]
- self.follow_car_history_state = objects[1]
-
- self.history_xs = [self.lead_car_history_state[:, 0], self.follow_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1], self.follow_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2], self.follow_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.object_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- # (2) set the xlim and ylim
- self.axis.set_xlim(-5, 50)
- self.axis.set_ylim(-2, 5)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.object_imgs.append(temp_img)
-
- traj_color_list = ["k", "m"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- self._draw_objects(i)
- self._draw_traj(i)
-
- return self.object_imgs, self.traj_imgs,
-
- def _draw_objects(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- for j in range(2):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[j][i],
- self.history_ys[j][i],
- 1.0,
- self.history_ths[j][i])
-
- self.object_imgs[fix_j].set_data([object_x, object_y])
- self.object_imgs[fix_j + 1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- for j in range(2):
- self.traj_imgs[j].set_data(self.history_xs[j][:i], self.history_ys[j][:i])
\ No newline at end of file
diff --git a/mpc/basic/main_ACC.py b/mpc/basic/main_ACC.py
deleted file mode 100644
index a868559..0000000
--- a/mpc/basic/main_ACC.py
+++ /dev/null
@@ -1,246 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- A = np.array([[0., V], [0., 0.]])
- B = np.array([[0.], [1.]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_ACC_TEMP.py b/mpc/basic/main_ACC_TEMP.py
deleted file mode 100644
index 9ad7c97..0000000
--- a/mpc/basic/main_ACC_TEMP.py
+++ /dev/null
@@ -1,243 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-# from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- Ad = np.array([[1., V * dt], [0., 1.]])
- Bd = np.array([[0.], [1. * dt]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- # sysc = matlab.ss(A, B, C, D)
- # discrete system
- # sysd = matlab.c2d(sysc, dt)
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_example.py b/mpc/basic/main_example.py
deleted file mode 100644
index b768a21..0000000
--- a/mpc/basic/main_example.py
+++ /dev/null
@@ -1,188 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_xs : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- D : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
- # print("xs = {0}".format(self.xs))
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
-def main():
- dt = 0.05
- simulation_time = 30 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- print(Ad)
- print(Bd)
- input()
-
- # evaluation function weight
- Q = np.diag([1., 1., 1., 1.])
- R = np.diag([1., 1.])
- pre_step = 10
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
- states = plant.xs
- opt_u = controller.calc_input(states, reference)
- plant.update_state(opt_u, dt=dt)
-
- history_states = np.array(plant.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 0])
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 1])
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 2])
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 3])
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us = np.array(controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 0])
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 1])
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_cvxopt.py b/mpc/basic/mpc_func_with_cvxopt.py
deleted file mode 100644
index 4e04736..0000000
--- a/mpc/basic/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,256 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_scipy.py b/mpc/basic/mpc_func_with_scipy.py
deleted file mode 100644
index 54ef3c9..0000000
--- a/mpc/basic/mpc_func_with_scipy.py
+++ /dev/null
@@ -1,262 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from scipy.optimize import minimize
-from scipy.optimize import LinearConstraint
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error) )
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- def optimized_func(dt_us):
- """
- """
- temp_dt_us = np.array([dt_us[i] for i in range(self.input_size * self.pre_step)])
-
- return (np.dot(temp_dt_us, np.dot(H, temp_dt_us.reshape(-1, 1))) - np.dot(G.T, temp_dt_us.reshape(-1, 1)))[0]
-
- # constraint
- lb = np.array([-np.inf for _ in range(len(ub))])
- linear_cons = LinearConstraint(A, lb, ub)
-
- init_dt_us = np.zeros(self.input_size * self.pre_step)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = minimize(optimized_func, init_dt_us, constraints=[linear_cons])
-
- opt_dt_us = opt_result.x
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/test_compare_methods.py b/mpc/basic/test_compare_methods.py
deleted file mode 100644
index 5ddaea4..0000000
--- a/mpc/basic/test_compare_methods.py
+++ /dev/null
@@ -1,211 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- states : float
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_state : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- C : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
-
- # print("xs = {0}".format(self.xs))
- # a = input()
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.history_xs)
-
-def main():
- dt = 0.05
- simulation_time = 50 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant_cvxopt = FirstOrderSystem(A, B, C, init_states=init_xs)
- plant_scipy = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1., 10., 10.])
- R = np.diag([0.01, 0.01])
- pre_step = 5
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller_cvxopt = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_scipy = MpcController_scipy(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_cvxopt.initialize_controller()
- controller_scipy.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
-
- states_cvxopt = plant_cvxopt.xs
- states_scipy = plant_scipy.xs
-
- opt_u_cvxopt = controller_cvxopt.calc_input(states_cvxopt, reference)
- opt_u_scipy = controller_scipy.calc_input(states_scipy, reference)
-
- plant_cvxopt.update_state(opt_u_cvxopt)
- plant_scipy.update_state(opt_u_scipy)
-
- history_states_cvxopt = np.array(plant_cvxopt.history_xs)
- history_states_scipy = np.array(plant_scipy.history_xs)
-
- time_history_fig = plt.figure(dpi=75)
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 0], label="cvxopt")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 0], label="scipy", linestyle="dashdot")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
- v_x_fig.legend()
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 1], label="cvxopt")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 1], label="scipy", linestyle="dashdot")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
- v_y_fig.legend()
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 2], label="cvxopt")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 2], label="scipy", linestyle="dashdot")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 3], label ="cvxopt")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 3], label="scipy", linestyle="dashdot")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us_cvxopt = np.array(controller_cvxopt.history_us)
- history_us_scipy = np.array(controller_scipy.history_us)
-
- input_history_fig = plt.figure(dpi=75)
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 0], label="cvxopt")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 0], label="scipy", linestyle="dashdot")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
- u_1_fig.legend()
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 1], label="cvxopt")
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 1], label="scipy", linestyle="dashdot")
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- u_2_fig.legend()
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/README.md b/mpc/extend/README.md
deleted file mode 100644
index e926aa5..0000000
--- a/mpc/extend/README.md
+++ /dev/null
@@ -1,41 +0,0 @@
-# Model Predictive Control for Vehicle model
-This program is for controlling the vehicle model.
-I implemented the steering control for vehicle by using Model Predictive Control.
-
-# Model
-Usually, the vehicle model is expressed by extremely complicated nonlinear equation.
-Acoording to reference 1, I used the simple model as shown in following equation.
-
-![\begin{align*} x[k+1] = x[k] + v\cos(\theta[k])dt \\ y[k+1] = y[k] + v\sin(\theta[k])dt \\ \theta[k+1] = \theta[k] + \frac{v \tan{\delta[k]}}{L}dt\\ \delta[k+1] = \delta[k] - \tau^{-1}(\delta[k]-\delta_{input})dt \end{align*}](https://latex.codecogs.com/gif.latex?\begin{align*}&space;x[k+1]&space;=&space;x[k]&space;+&space;v\cos(\theta[k])dt&space;\\&space;y[k+1]&space;=&space;y[k]&space;+&space;v\sin(\theta[k])dt&space;\\&space;\theta[k+1]&space;=&space;\theta[k]&space;+&space;\frac{v&space;\tan{\delta[k]}}{L}dt\\&space;\delta[k+1]&space;=&space;\delta[k]&space;-&space;\tau^{-1}(\delta[k]-\delta_{input})dt&space;\end{align*}) -
-However, it is still a nonlinear equation.
-Therefore, I assume that the car is tracking the reference trajectory.
-If we get the assumption, the model can turn to linear model by using the path's curvatures.
-
-
-
-However, it is still a nonlinear equation.
-Therefore, I assume that the car is tracking the reference trajectory.
-If we get the assumption, the model can turn to linear model by using the path's curvatures.
-
-![\boldsymbol{X}[k+1] = \begin{bmatrix} 1 & vdt & 0 \\ 0 & 1 & \frac{vdt}{L \ cos^{2} \delta_r} \\ 0 & 0 & 1 - \tau^{-1}dt\\ \end{bmatrix} \begin{bmatrix} y[k] \\ \theta[k] \\ \delta[k] \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ \tau^{-1}dt \\ \end{bmatrix} \delta_{input} - \begin{bmatrix} 0 \\ -\frac{v \delta_r dt}{L \ cos^{2} \delta_r} \\ 0 \\ \end{bmatrix}](https://latex.codecogs.com/gif.latex?\boldsymbol{X}[k+1]&space;=&space;\begin{bmatrix}&space;1&space;&&space;vdt&space;&&space;0&space;\\&space;0&space;&&space;1&space;&&space;\frac{vdt}{L&space;\&space;cos^{2}&space;\delta_r}&space;\\&space;0&space;&&space;0&space;&&space;1&space;-&space;\tau^{-1}dt\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;y[k]&space;\\&space;\theta[k]&space;\\&space;\delta[k]&space;\end{bmatrix}&space;+&space;\begin{bmatrix}&space;0&space;\\&space;0&space;\\&space;\tau^{-1}dt&space;\\&space;\end{bmatrix}&space;\delta_{input}&space;-&space;\begin{bmatrix}&space;0&space;\\&space;-\frac{v&space;\delta_r&space;dt}{L&space;\&space;cos^{2}&space;\delta_r}&space;\\&space;0&space;\\&space;\end{bmatrix}) -
-and \delta_r denoted
-
-
-
-and \delta_r denoted
-
-) -
-R is the curvatures of the reference trajectory.
-
-Now we can get the linear state equation and can apply the MPC theory.
-
-However, you should care that this state euation could be changed during the predict horizon.
-I implemented this, so if you know about the detail please go to "IteraticeMPC_func.py"
-
-# Expected Results
-
-
-
-R is the curvatures of the reference trajectory.
-
-Now we can get the linear state equation and can apply the MPC theory.
-
-However, you should care that this state euation could be changed during the predict horizon.
-I implemented this, so if you know about the detail please go to "IteraticeMPC_func.py"
-
-# Expected Results
-
- -
-
-
- -
-# Usage
-
-```
-$ python main_track.py
-```
-
-# Reference
-- 1. https://qiita.com/taka_horibe/items/47f86e02e2db83b0c570#%E8%BB%8A%E4%B8%A1%E3%81%AE%E8%BB%8C%E9%81%93%E8%BF%BD%E5%BE%93%E5%95%8F%E9%A1%8C%E9%9D%9E%E7%B7%9A%E5%BD%A2%E3%81%AB%E9%81%A9%E7%94%A8%E3%81%99%E3%82%8B (Japanese)
diff --git a/mpc/extend/animation.py b/mpc/extend/animation.py
deleted file mode 100755
index a085b5a..0000000
--- a/mpc/extend/animation.py
+++ /dev/null
@@ -1,324 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.lead_car_history_state = objects[0]
- self.lead_car_history_predict_state = objects[1]
- self.traj = objects[2]
- self.history_traj_ref = objects[3]
- self.history_angle_ref = objects[4]
-
- self.history_xs = [self.lead_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
- self.predict_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 5
- HIGH_MARGIN = 5
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], ".", color="m")
- self.traj_imgs.append(temp_img)
-
- # predict
- for _ in range(2 * len(self.history_angle_ref[0])):
- temp_img, = self.axis.plot([],[], color="g", linewidth=0.5) # point
- # temp_img, = self.axis.plot([],[], ".", color="g", linewidth=0.5) # point
- self.predict_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs, self.predict_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 5.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # all traj_ref
- self.traj_imgs[1].set_data(self.traj[0, :], self.traj[1, :])
-
- # traj_ref
- # self.traj_imgs[2].set_data(self.history_traj_ref[i][0, :], self.history_traj_ref[i][1, :])
-
- def _draw_prediction(self, i):
- """draw prediction
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
-
- for j in range(0, len(self.history_angle_ref[0]), 4):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y =\
- circle_make_with_angles(self.lead_car_history_predict_state[i][j, 0],
- self.lead_car_history_predict_state[i][j, 1], 1.,
- self.lead_car_history_predict_state[i][j, 2])
-
- self.predict_imgs[fix_j].set_data(object_x, object_y)
- self.predict_imgs[fix_j + 1].set_data(angle_x, angle_y)
\ No newline at end of file
diff --git a/mpc/extend/coordinate_trans.py b/mpc/extend/coordinate_trans.py
deleted file mode 100755
index 9cfa220..0000000
--- a/mpc/extend/coordinate_trans.py
+++ /dev/null
@@ -1,112 +0,0 @@
-import math
-import numpy as np
-import copy
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def coordinate_transformation_in_position(positions, base_positions):
- '''
- Transformation the coordinate in the positions
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_positions : numpy.ndarray
- this parameter is composed of x, y
- shoulg have (2, 1) shape
-
- Returns
- -------
- traslated_positions : numpy.ndarray, shape(2, N)
-
- '''
-
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- base_positions = np.array(base_positions)
- base_positions = base_positions.reshape(2, 1)
-
- translated_positions = positions - base_positions
-
- return translated_positions
-
-
-def coordinate_transformation_in_matrix_angles(positions, base_angles):
- '''
- Transformation the coordinate in the matrix angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- translated_positions = np.zeros_like(positions)
-
- for i in range(len(base_angles)):
- rot_matrix = [[np.cos(base_angles[i]), np.sin(base_angles[i])],
- [-1*np.sin(base_angles[i]), np.cos(base_angles[i])]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_position = np.dot(rot_matrix, positions[:, i].reshape(2, 1))
-
- translated_positions[:, i] = translated_position.flatten()
-
- return translated_positions.reshape(2, -1)
-
-# def coordinate_inv_transformation
-if __name__ == '__main__':
- positions_1 = np.array([[1.0], [2.0]])
- base_angle = 1.25
-
- translated_positions_1 = coordinate_transformation_in_angle(positions_1, base_angle)
- print(translated_positions_1)
-
diff --git a/mpc/extend/extended_MPC.py b/mpc/extend/extended_MPC.py
deleted file mode 100644
index c365aaf..0000000
--- a/mpc/extend/extended_MPC.py
+++ /dev/null
@@ -1,306 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-import cvxopt
-cvxopt.solvers.options['show_progress'] = False # not display
-
-class IterativeMpcController():
- """
- Attributes
- ------------
- Ad_s : list of numpy.ndarray
- system matrix
- Bd_s : list of numpy.ndarray
- input matrix
- W_D_s : list of numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, system_model, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- system_model : SystemModel class
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.Ad_s[0].shape[0]
- self.input_size = self.Bd_s[0].shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.Ad_s[0]]
-
- self.phi_mat = copy.deepcopy(self.Ad_s[0])
-
- for i in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.Ad_s[i + 1])
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- # print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.Bd_s[0])
- gammma_mat_temp = copy.deepcopy(self.Bd_s[0])
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.Bd_s[i + 1])
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- # print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- # print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- # print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- # print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- # print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D_s[0])
-
- for i in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D_s[i + 1]))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- # print("Qs = \n{0}".format(self.Qs))
- # print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- # print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- # print("F = \n{0}".format(self.F))
- # print("F1 = \n{0}".format(self.F1))
- # print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- # print("W = \n{0}".format(self.W))
- # print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_u : numpy.ndarray, shape(input_length, )
- optimal input
- all_opt_u : numpy.ndarray, shape(PREDICT_STEP, input_length)
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # calc all predit u
- all_opt_u = [copy.deepcopy(opt_u)]
- temp_u = copy.deepcopy(opt_u)
-
- for i in range(1, self.pre_step):
- temp_u += opt_dt_us[i * self.input_size: (i + 1) * self.input_size]
- all_opt_u.append(copy.deepcopy(temp_u))
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u, np.array(all_opt_u)
-
- def update_system_model(self, system_model):
- """update system model
- Parameters
- -----------
- system_model : SystemModel class
- """
-
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
-
- self.initialize_controller()
diff --git a/mpc/extend/func_curvature.py b/mpc/extend/func_curvature.py
deleted file mode 100644
index cdd99e6..0000000
--- a/mpc/extend/func_curvature.py
+++ /dev/null
@@ -1,182 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-import random
-
-from traj_func import make_sample_traj
-
-def calc_curvature(points):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape (2, 3)
- these points should follow subseqently
-
- Returns
- ----------
- curvature : float
- """
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.show()
- """
-
- return 1. / R
-
-def calc_curvatures(traj_ref, predict_step, num_skip):
- """
- Parameters
- -----------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- predict_step : int
- predict step
- num_skip : int
- skip_num
-
- Returns
- ----------
- angles : list
- curvature : list
- """
-
- angles = []
- curvatures = []
-
- for i in range(predict_step):
- # make pairs
- points = np.zeros((2, 3))
-
- points[:, 0] = traj_ref[:, i]
- points[:, 1] = traj_ref[:, i + num_skip]
- points[:, 2] = traj_ref[:, i + 2 * num_skip]
-
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- # calc R
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- # add
- diff = points[:, 2] - points[:, 0]
- angles.append(math.atan2(diff[1], diff[0]))
- curvatures.append(1. / R)
-
- # plot
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for x in np.arange(-5, 5, 0.01):
- plot_points_x.append(x)
- plot_points_y.append(x * math.tan(angles[-1]))
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.xlim(-1, 10)
- plt.ylim(-1, 2)
-
- plt.show()
- """
-
- return angles, curvatures
-
-def calc_ideal_vel(traj_ref, dt):
- """
- Parameters
- ------------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- dt : float
- sampling time of system
- """
- # end point and start point
- diff = traj_ref[:, -1] - traj_ref[:, 0]
- distance = np.sqrt(np.sum(diff**2))
-
- V = distance / (dt * traj_ref.shape[1])
-
- return V
-
-def main():
- """
- points = np.zeros((2, 3))
- points[:, 0] = np.array([1. + random.random(), random.random()])
-
- points[:, 1] = np.array([random.random(), 3 + random.random()])
-
- points[:, 2] = np.array([3 + random.random(), -3 + random.random()])
-
- calc_cuvature(points)
- """
-
- traj_ref_xs, traj_ref_ys = make_sample_traj(1000)
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- calc_curvatures(traj_ref[:, 10:10 + 15 + 100 * 2], 15, 100)
-
-
-if __name__ == "__main__":
- main()
-
-
-
-
-
diff --git a/mpc/extend/main_track.py b/mpc/extend/main_track.py
deleted file mode 100644
index f78413f..0000000
--- a/mpc/extend/main_track.py
+++ /dev/null
@@ -1,464 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-# from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from extended_MPC import IterativeMpcController
-from animation import AnimDrawer
-# from control import matlab
-from coordinate_trans import coordinate_transformation_in_angle, coordinate_transformation_in_position
-from traj_func import make_sample_traj
-from func_curvature import calc_curvatures, calc_ideal_vel
-
-class WheeledSystem():
- """SampleSystem, this is the simulator
- Kinematic model of car
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, phi, beta]
- history_xs : list
- time history of state
- tau : float
- time constant of tire
- FRONT_WHEEL_BASE : float
- REAR_WHEEL_BASE : float
- predict_xs :
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.NUM_STATE = 4
- self.xs = np.zeros(self.NUM_STATE)
-
- self.tau = 0.01
-
- self.FRONT_WHEELE_BASE = 1.0
- self.REAR_WHEELE_BASE = 1.0
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], self.xs[3], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., self.xs[3] + k0[3]/2, us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k1[0]/2., self.xs[1] + k1[1]/2., self.xs[2] + k1[2]/2., self.xs[3] + k1[3]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], self.xs[3] + k2[3], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- self.xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.xs)
-
- def predict_state(self, us, dt=0.01):
- """make predict state by using optimal input made by MPC
- Paramaters
- -----------
- us : array-like, shape(2, N)
- optimal input made by MPC
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
-
- xs = copy.deepcopy(self.xs)
- predict_xs = [copy.deepcopy(xs)]
-
- for i in range(us.shape[1]):
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(xs[0], xs[1], xs[2], xs[3], us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(xs[0] + k0[0]/2., xs[1] + k0[1]/2., xs[2] + k0[2]/2., xs[3] + k0[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(xs[0] + k1[0]/2., xs[1] + k1[1]/2., xs[2] + k1[2]/2., xs[3] + k1[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(xs[0] + k2[0], xs[1] + k2[1], xs[2] + k2[2], xs[3] + k2[3], us[0, i], us[1, i])
-
- xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- predict_xs.append(copy.deepcopy(xs))
-
- self.history_predict_xs.append(np.array(predict_xs))
-
- def _func_x_1(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.cos(y_3 + y_4)
- y_dot = u_1 * math.cos(y_3)
-
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.sin(y_3 + y_4)
- y_dot = u_1 * math.sin(y_3)
-
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 / self.REAR_WHEELE_BASE * math.sin(y_4)
- y_dot = u_1 * math.tan(y_4) / (self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
-
- return y_dot
-
- def _func_x_4(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """Ad, Bd, W_D, Q, R
- ParAd, Bd, W_D, Q, R
- ---Ad, Bd, W_D, Q, R
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = math.atan2(self.REAR_WHEELE_BASE * math.tan(u_2) ,self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
- y_dot = - 1. / self.tau * (y_4 - u_2)
-
- return y_dot
-
-class SystemModel():
- """
- Attributes
- -----------
- WHEEL_BASE : float
- wheel base of the car
- Ad_s : list
- list of system model matrix Ad
- Bd_s : list
- list of system model matrix Bd
- W_D_s : list
- list of system model matrix W_D_s
- Q : numpy.ndarray
- R : numpy.ndarray
- """
- def __init__(self, tau = 0.01, dt = 0.01):
- """
- Parameters
- -----------
- tau : time constant, optional
- dt : sampling time, optional
- """
- self.dt = dt
- self.tau = tau
- self.WHEEL_BASE = 2.2
-
- self.Ad_s = []
- self.Bd_s = []
- self.W_D_s = []
-
- def calc_predict_sytem_model(self, V, curvatures, predict_step):
- """
- calc next predict systemo models
- V : float
- current speed of car
- curvatures : list
- this is the next curvature's list
- predict_step : int
- predict step of MPC
- """
- for i in range(predict_step):
- delta_r = math.atan2(self.WHEEL_BASE, 1. / curvatures[i])
-
- A12 = (V / self.WHEEL_BASE) / (math.cos(delta_r)**2)
- A22 = (1. - 1. / self.tau * self.dt)
-
- Ad = np.array([[1., V * self.dt, 0.],
- [0., 1., A12 * self.dt],
- [0., 0., A22]])
-
- Bd = np.array([[0.], [0.], [1. / self.tau]]) * self.dt
-
- # -v*curvature + v/L*(tan(delta_r)-delta_r*cos_delta_r_squared_inv);
- # W_D_0 = V / self.WHEEL_BASE * (delta_r / (math.cos(delta_r)**2)
- W_D_0 = -V * curvatures[i] + (V / self.WHEEL_BASE) * (math.tan(delta_r) - delta_r / (math.cos(delta_r)**2))
-
- W_D = np.array([[0.], [W_D_0], [0.]]) * self.dt
-
- self.Ad_s.append(Ad)
- self.Bd_s.append(Bd)
- self.W_D_s.append(W_D)
-
- # return self.Ad_s, self.Bd_s, self.W_D_s
-
-def search_nearest_point(points, base_point):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape is (2, N)
- base_point : numpy.ndarray, shape is (2, 1)
-
- Returns
- -------
- nearest_index :
- nearest_point :
- """
- distance_mat = np.sqrt(np.sum((points - base_point)**2, axis=0))
-
- index_min = np.argmin(distance_mat)
-
- return index_min, points[:, index_min]
-
-
-def main():
- # parameters
- dt = 0.01
- simulation_time = 20 # in seconds
- PREDICT_STEP = 30
- iteration_num = int(simulation_time / dt)
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([0., 0., math.pi/5, 0.])
- lead_car = WheeledSystem(init_states=init_xs_lead)
-
- # make system model
- lead_car_system_model = SystemModel()
-
- # reference
- history_traj_ref = []
- history_angle_ref = []
- traj_ref_xs, traj_ref_ys = make_sample_traj(int(simulation_time/dt))
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # get traj's curvature
- NUM_SKIP = 3
- MARGIN = 50
- angles, curvatures = calc_curvatures(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save traj ref
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # print(history_traj_ref)
- # input()
-
- # evaluation function weight
- Q = np.diag([1e2, 1., 1e3])
- R = np.diag([1e2])
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # make controller with discreted matrix
- lead_controller = IterativeMpcController(lead_car_system_model, Q, R, PREDICT_STEP,
- dt_input_upper=np.array([1 * dt]), dt_input_lower=np.array([-1 * dt]),
- input_upper=np.array([1.]), input_lower=np.array([-1.]))
-
-
- # initialize
- lead_controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
-
- ## lead
- # world traj
- lead_states = lead_car.xs
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # end check
- if len(traj_ref_ys) <= index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN:
- print("break")
- break
-
- # get traj's curvature
- angles, curvatures = calc_curvatures(traj_ref[:, index_min+MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # transformation
- # car
- relative_car_position = coordinate_transformation_in_position(lead_states[:2].reshape(2, 1), nearest_point)
- relative_car_position = coordinate_transformation_in_angle(relative_car_position, angles[0])
-
- relative_car_angle = lead_states[2] - angles[0]
- relative_car_state = np.hstack((relative_car_position[1], relative_car_angle, lead_states[-1]))
-
- # traj_ref
- relative_traj = coordinate_transformation_in_position(traj_ref[:, index_min:index_min + PREDICT_STEP], nearest_point)
- relative_traj = coordinate_transformation_in_angle(relative_traj, angles[0])
- relative_ref_angle = np.array(angles) - angles[0]
-
- # make ref
- lead_reference = np.array([[relative_traj[1, -1], relative_ref_angle[-1], 0.] for i in range(PREDICT_STEP)]).flatten()
-
- print("relative car state = {}".format(relative_car_state))
- print("nearest point = {}".format(nearest_point))
- # input()
-
- # update system matrix
- lead_controller.update_system_model(lead_car_system_model)
-
- lead_opt_u, all_opt_u = lead_controller.calc_input(relative_car_state, lead_reference)
-
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- all_opt_u = np.stack((np.ones(PREDICT_STEP)*V, all_opt_u.flatten()))
-
- print("opt_u = {}".format(lead_opt_u))
- print("all_opt_u = {}".format(all_opt_u))
-
- # predict
- lead_car.predict_state(all_opt_u, dt=dt)
-
- # update
- lead_car.update_state(lead_opt_u, dt=dt)
-
- # print(lead_car.history_predict_xs)
- # input()
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- lead_history_predict_states = lead_car.history_predict_xs
-
- """
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
- """
-
- animdrawer = AnimDrawer([lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/mpc_func_with_cvxopt.py b/mpc/extend/mpc_func_with_cvxopt.py
deleted file mode 100644
index a46d2d2..0000000
--- a/mpc/extend/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,304 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, W_D, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.W_D = np.array(W_D)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D)
-
- for _ in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
-
- def update_system_model(self, A, B, W_D):
- """update system model
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- """
-
- self.A = A
- self.B = B
- self.W_D = W_D
-
- self.initialize_controller()
diff --git a/mpc/extend/traj_func.py b/mpc/extend/traj_func.py
deleted file mode 100644
index 8f5ce18..0000000
--- a/mpc/extend/traj_func.py
+++ /dev/null
@@ -1,31 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-def make_sample_traj(NUM, dt=0.01, a=30.):
- """
- make sample trajectory
- Parameters
- ------------
- NUM : int
- dt : float
- a : float
-
- Returns
- ----------
- traj_xs : list
- traj_ys : list
- """
- DELAY = 2.
- traj_xs = []
- traj_ys = []
-
- for i in range(NUM):
- traj_xs.append(i * 0.1)
- traj_ys.append(a * math.sin(dt * i / DELAY))
-
- plt.plot(traj_xs, traj_ys)
- plt.show()
-
- return traj_xs, traj_ys
-
diff --git a/nmpc/cgmres/README.md b/nmpc/cgmres/README.md
deleted file mode 100644
index a46901c..0000000
--- a/nmpc/cgmres/README.md
+++ /dev/null
@@ -1,79 +0,0 @@
-# CGMRES method of Nonlinear Model Predictive Control
-This program is about Continuous gmres method for NMPC
-Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
-By using CGMRES, we can pass the calculating step and get the optimal input quickly.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
-
-
-# Usage
-
-```
-$ python main_track.py
-```
-
-# Reference
-- 1. https://qiita.com/taka_horibe/items/47f86e02e2db83b0c570#%E8%BB%8A%E4%B8%A1%E3%81%AE%E8%BB%8C%E9%81%93%E8%BF%BD%E5%BE%93%E5%95%8F%E9%A1%8C%E9%9D%9E%E7%B7%9A%E5%BD%A2%E3%81%AB%E9%81%A9%E7%94%A8%E3%81%99%E3%82%8B (Japanese)
diff --git a/mpc/extend/animation.py b/mpc/extend/animation.py
deleted file mode 100755
index a085b5a..0000000
--- a/mpc/extend/animation.py
+++ /dev/null
@@ -1,324 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.lead_car_history_state = objects[0]
- self.lead_car_history_predict_state = objects[1]
- self.traj = objects[2]
- self.history_traj_ref = objects[3]
- self.history_angle_ref = objects[4]
-
- self.history_xs = [self.lead_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
- self.predict_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 5
- HIGH_MARGIN = 5
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], ".", color="m")
- self.traj_imgs.append(temp_img)
-
- # predict
- for _ in range(2 * len(self.history_angle_ref[0])):
- temp_img, = self.axis.plot([],[], color="g", linewidth=0.5) # point
- # temp_img, = self.axis.plot([],[], ".", color="g", linewidth=0.5) # point
- self.predict_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs, self.predict_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 5.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # all traj_ref
- self.traj_imgs[1].set_data(self.traj[0, :], self.traj[1, :])
-
- # traj_ref
- # self.traj_imgs[2].set_data(self.history_traj_ref[i][0, :], self.history_traj_ref[i][1, :])
-
- def _draw_prediction(self, i):
- """draw prediction
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
-
- for j in range(0, len(self.history_angle_ref[0]), 4):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y =\
- circle_make_with_angles(self.lead_car_history_predict_state[i][j, 0],
- self.lead_car_history_predict_state[i][j, 1], 1.,
- self.lead_car_history_predict_state[i][j, 2])
-
- self.predict_imgs[fix_j].set_data(object_x, object_y)
- self.predict_imgs[fix_j + 1].set_data(angle_x, angle_y)
\ No newline at end of file
diff --git a/mpc/extend/coordinate_trans.py b/mpc/extend/coordinate_trans.py
deleted file mode 100755
index 9cfa220..0000000
--- a/mpc/extend/coordinate_trans.py
+++ /dev/null
@@ -1,112 +0,0 @@
-import math
-import numpy as np
-import copy
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def coordinate_transformation_in_position(positions, base_positions):
- '''
- Transformation the coordinate in the positions
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_positions : numpy.ndarray
- this parameter is composed of x, y
- shoulg have (2, 1) shape
-
- Returns
- -------
- traslated_positions : numpy.ndarray, shape(2, N)
-
- '''
-
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- base_positions = np.array(base_positions)
- base_positions = base_positions.reshape(2, 1)
-
- translated_positions = positions - base_positions
-
- return translated_positions
-
-
-def coordinate_transformation_in_matrix_angles(positions, base_angles):
- '''
- Transformation the coordinate in the matrix angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- translated_positions = np.zeros_like(positions)
-
- for i in range(len(base_angles)):
- rot_matrix = [[np.cos(base_angles[i]), np.sin(base_angles[i])],
- [-1*np.sin(base_angles[i]), np.cos(base_angles[i])]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_position = np.dot(rot_matrix, positions[:, i].reshape(2, 1))
-
- translated_positions[:, i] = translated_position.flatten()
-
- return translated_positions.reshape(2, -1)
-
-# def coordinate_inv_transformation
-if __name__ == '__main__':
- positions_1 = np.array([[1.0], [2.0]])
- base_angle = 1.25
-
- translated_positions_1 = coordinate_transformation_in_angle(positions_1, base_angle)
- print(translated_positions_1)
-
diff --git a/mpc/extend/extended_MPC.py b/mpc/extend/extended_MPC.py
deleted file mode 100644
index c365aaf..0000000
--- a/mpc/extend/extended_MPC.py
+++ /dev/null
@@ -1,306 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-import cvxopt
-cvxopt.solvers.options['show_progress'] = False # not display
-
-class IterativeMpcController():
- """
- Attributes
- ------------
- Ad_s : list of numpy.ndarray
- system matrix
- Bd_s : list of numpy.ndarray
- input matrix
- W_D_s : list of numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, system_model, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- system_model : SystemModel class
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.Ad_s[0].shape[0]
- self.input_size = self.Bd_s[0].shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.Ad_s[0]]
-
- self.phi_mat = copy.deepcopy(self.Ad_s[0])
-
- for i in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.Ad_s[i + 1])
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- # print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.Bd_s[0])
- gammma_mat_temp = copy.deepcopy(self.Bd_s[0])
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.Bd_s[i + 1])
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- # print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- # print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- # print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- # print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- # print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D_s[0])
-
- for i in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D_s[i + 1]))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- # print("Qs = \n{0}".format(self.Qs))
- # print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- # print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- # print("F = \n{0}".format(self.F))
- # print("F1 = \n{0}".format(self.F1))
- # print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- # print("W = \n{0}".format(self.W))
- # print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_u : numpy.ndarray, shape(input_length, )
- optimal input
- all_opt_u : numpy.ndarray, shape(PREDICT_STEP, input_length)
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # calc all predit u
- all_opt_u = [copy.deepcopy(opt_u)]
- temp_u = copy.deepcopy(opt_u)
-
- for i in range(1, self.pre_step):
- temp_u += opt_dt_us[i * self.input_size: (i + 1) * self.input_size]
- all_opt_u.append(copy.deepcopy(temp_u))
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u, np.array(all_opt_u)
-
- def update_system_model(self, system_model):
- """update system model
- Parameters
- -----------
- system_model : SystemModel class
- """
-
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
-
- self.initialize_controller()
diff --git a/mpc/extend/func_curvature.py b/mpc/extend/func_curvature.py
deleted file mode 100644
index cdd99e6..0000000
--- a/mpc/extend/func_curvature.py
+++ /dev/null
@@ -1,182 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-import random
-
-from traj_func import make_sample_traj
-
-def calc_curvature(points):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape (2, 3)
- these points should follow subseqently
-
- Returns
- ----------
- curvature : float
- """
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.show()
- """
-
- return 1. / R
-
-def calc_curvatures(traj_ref, predict_step, num_skip):
- """
- Parameters
- -----------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- predict_step : int
- predict step
- num_skip : int
- skip_num
-
- Returns
- ----------
- angles : list
- curvature : list
- """
-
- angles = []
- curvatures = []
-
- for i in range(predict_step):
- # make pairs
- points = np.zeros((2, 3))
-
- points[:, 0] = traj_ref[:, i]
- points[:, 1] = traj_ref[:, i + num_skip]
- points[:, 2] = traj_ref[:, i + 2 * num_skip]
-
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- # calc R
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- # add
- diff = points[:, 2] - points[:, 0]
- angles.append(math.atan2(diff[1], diff[0]))
- curvatures.append(1. / R)
-
- # plot
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for x in np.arange(-5, 5, 0.01):
- plot_points_x.append(x)
- plot_points_y.append(x * math.tan(angles[-1]))
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.xlim(-1, 10)
- plt.ylim(-1, 2)
-
- plt.show()
- """
-
- return angles, curvatures
-
-def calc_ideal_vel(traj_ref, dt):
- """
- Parameters
- ------------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- dt : float
- sampling time of system
- """
- # end point and start point
- diff = traj_ref[:, -1] - traj_ref[:, 0]
- distance = np.sqrt(np.sum(diff**2))
-
- V = distance / (dt * traj_ref.shape[1])
-
- return V
-
-def main():
- """
- points = np.zeros((2, 3))
- points[:, 0] = np.array([1. + random.random(), random.random()])
-
- points[:, 1] = np.array([random.random(), 3 + random.random()])
-
- points[:, 2] = np.array([3 + random.random(), -3 + random.random()])
-
- calc_cuvature(points)
- """
-
- traj_ref_xs, traj_ref_ys = make_sample_traj(1000)
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- calc_curvatures(traj_ref[:, 10:10 + 15 + 100 * 2], 15, 100)
-
-
-if __name__ == "__main__":
- main()
-
-
-
-
-
diff --git a/mpc/extend/main_track.py b/mpc/extend/main_track.py
deleted file mode 100644
index f78413f..0000000
--- a/mpc/extend/main_track.py
+++ /dev/null
@@ -1,464 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-# from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from extended_MPC import IterativeMpcController
-from animation import AnimDrawer
-# from control import matlab
-from coordinate_trans import coordinate_transformation_in_angle, coordinate_transformation_in_position
-from traj_func import make_sample_traj
-from func_curvature import calc_curvatures, calc_ideal_vel
-
-class WheeledSystem():
- """SampleSystem, this is the simulator
- Kinematic model of car
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, phi, beta]
- history_xs : list
- time history of state
- tau : float
- time constant of tire
- FRONT_WHEEL_BASE : float
- REAR_WHEEL_BASE : float
- predict_xs :
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.NUM_STATE = 4
- self.xs = np.zeros(self.NUM_STATE)
-
- self.tau = 0.01
-
- self.FRONT_WHEELE_BASE = 1.0
- self.REAR_WHEELE_BASE = 1.0
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], self.xs[3], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., self.xs[3] + k0[3]/2, us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k1[0]/2., self.xs[1] + k1[1]/2., self.xs[2] + k1[2]/2., self.xs[3] + k1[3]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], self.xs[3] + k2[3], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- self.xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.xs)
-
- def predict_state(self, us, dt=0.01):
- """make predict state by using optimal input made by MPC
- Paramaters
- -----------
- us : array-like, shape(2, N)
- optimal input made by MPC
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
-
- xs = copy.deepcopy(self.xs)
- predict_xs = [copy.deepcopy(xs)]
-
- for i in range(us.shape[1]):
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(xs[0], xs[1], xs[2], xs[3], us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(xs[0] + k0[0]/2., xs[1] + k0[1]/2., xs[2] + k0[2]/2., xs[3] + k0[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(xs[0] + k1[0]/2., xs[1] + k1[1]/2., xs[2] + k1[2]/2., xs[3] + k1[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(xs[0] + k2[0], xs[1] + k2[1], xs[2] + k2[2], xs[3] + k2[3], us[0, i], us[1, i])
-
- xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- predict_xs.append(copy.deepcopy(xs))
-
- self.history_predict_xs.append(np.array(predict_xs))
-
- def _func_x_1(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.cos(y_3 + y_4)
- y_dot = u_1 * math.cos(y_3)
-
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.sin(y_3 + y_4)
- y_dot = u_1 * math.sin(y_3)
-
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 / self.REAR_WHEELE_BASE * math.sin(y_4)
- y_dot = u_1 * math.tan(y_4) / (self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
-
- return y_dot
-
- def _func_x_4(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """Ad, Bd, W_D, Q, R
- ParAd, Bd, W_D, Q, R
- ---Ad, Bd, W_D, Q, R
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = math.atan2(self.REAR_WHEELE_BASE * math.tan(u_2) ,self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
- y_dot = - 1. / self.tau * (y_4 - u_2)
-
- return y_dot
-
-class SystemModel():
- """
- Attributes
- -----------
- WHEEL_BASE : float
- wheel base of the car
- Ad_s : list
- list of system model matrix Ad
- Bd_s : list
- list of system model matrix Bd
- W_D_s : list
- list of system model matrix W_D_s
- Q : numpy.ndarray
- R : numpy.ndarray
- """
- def __init__(self, tau = 0.01, dt = 0.01):
- """
- Parameters
- -----------
- tau : time constant, optional
- dt : sampling time, optional
- """
- self.dt = dt
- self.tau = tau
- self.WHEEL_BASE = 2.2
-
- self.Ad_s = []
- self.Bd_s = []
- self.W_D_s = []
-
- def calc_predict_sytem_model(self, V, curvatures, predict_step):
- """
- calc next predict systemo models
- V : float
- current speed of car
- curvatures : list
- this is the next curvature's list
- predict_step : int
- predict step of MPC
- """
- for i in range(predict_step):
- delta_r = math.atan2(self.WHEEL_BASE, 1. / curvatures[i])
-
- A12 = (V / self.WHEEL_BASE) / (math.cos(delta_r)**2)
- A22 = (1. - 1. / self.tau * self.dt)
-
- Ad = np.array([[1., V * self.dt, 0.],
- [0., 1., A12 * self.dt],
- [0., 0., A22]])
-
- Bd = np.array([[0.], [0.], [1. / self.tau]]) * self.dt
-
- # -v*curvature + v/L*(tan(delta_r)-delta_r*cos_delta_r_squared_inv);
- # W_D_0 = V / self.WHEEL_BASE * (delta_r / (math.cos(delta_r)**2)
- W_D_0 = -V * curvatures[i] + (V / self.WHEEL_BASE) * (math.tan(delta_r) - delta_r / (math.cos(delta_r)**2))
-
- W_D = np.array([[0.], [W_D_0], [0.]]) * self.dt
-
- self.Ad_s.append(Ad)
- self.Bd_s.append(Bd)
- self.W_D_s.append(W_D)
-
- # return self.Ad_s, self.Bd_s, self.W_D_s
-
-def search_nearest_point(points, base_point):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape is (2, N)
- base_point : numpy.ndarray, shape is (2, 1)
-
- Returns
- -------
- nearest_index :
- nearest_point :
- """
- distance_mat = np.sqrt(np.sum((points - base_point)**2, axis=0))
-
- index_min = np.argmin(distance_mat)
-
- return index_min, points[:, index_min]
-
-
-def main():
- # parameters
- dt = 0.01
- simulation_time = 20 # in seconds
- PREDICT_STEP = 30
- iteration_num = int(simulation_time / dt)
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([0., 0., math.pi/5, 0.])
- lead_car = WheeledSystem(init_states=init_xs_lead)
-
- # make system model
- lead_car_system_model = SystemModel()
-
- # reference
- history_traj_ref = []
- history_angle_ref = []
- traj_ref_xs, traj_ref_ys = make_sample_traj(int(simulation_time/dt))
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # get traj's curvature
- NUM_SKIP = 3
- MARGIN = 50
- angles, curvatures = calc_curvatures(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save traj ref
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # print(history_traj_ref)
- # input()
-
- # evaluation function weight
- Q = np.diag([1e2, 1., 1e3])
- R = np.diag([1e2])
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # make controller with discreted matrix
- lead_controller = IterativeMpcController(lead_car_system_model, Q, R, PREDICT_STEP,
- dt_input_upper=np.array([1 * dt]), dt_input_lower=np.array([-1 * dt]),
- input_upper=np.array([1.]), input_lower=np.array([-1.]))
-
-
- # initialize
- lead_controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
-
- ## lead
- # world traj
- lead_states = lead_car.xs
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # end check
- if len(traj_ref_ys) <= index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN:
- print("break")
- break
-
- # get traj's curvature
- angles, curvatures = calc_curvatures(traj_ref[:, index_min+MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # transformation
- # car
- relative_car_position = coordinate_transformation_in_position(lead_states[:2].reshape(2, 1), nearest_point)
- relative_car_position = coordinate_transformation_in_angle(relative_car_position, angles[0])
-
- relative_car_angle = lead_states[2] - angles[0]
- relative_car_state = np.hstack((relative_car_position[1], relative_car_angle, lead_states[-1]))
-
- # traj_ref
- relative_traj = coordinate_transformation_in_position(traj_ref[:, index_min:index_min + PREDICT_STEP], nearest_point)
- relative_traj = coordinate_transformation_in_angle(relative_traj, angles[0])
- relative_ref_angle = np.array(angles) - angles[0]
-
- # make ref
- lead_reference = np.array([[relative_traj[1, -1], relative_ref_angle[-1], 0.] for i in range(PREDICT_STEP)]).flatten()
-
- print("relative car state = {}".format(relative_car_state))
- print("nearest point = {}".format(nearest_point))
- # input()
-
- # update system matrix
- lead_controller.update_system_model(lead_car_system_model)
-
- lead_opt_u, all_opt_u = lead_controller.calc_input(relative_car_state, lead_reference)
-
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- all_opt_u = np.stack((np.ones(PREDICT_STEP)*V, all_opt_u.flatten()))
-
- print("opt_u = {}".format(lead_opt_u))
- print("all_opt_u = {}".format(all_opt_u))
-
- # predict
- lead_car.predict_state(all_opt_u, dt=dt)
-
- # update
- lead_car.update_state(lead_opt_u, dt=dt)
-
- # print(lead_car.history_predict_xs)
- # input()
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- lead_history_predict_states = lead_car.history_predict_xs
-
- """
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
- """
-
- animdrawer = AnimDrawer([lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/mpc_func_with_cvxopt.py b/mpc/extend/mpc_func_with_cvxopt.py
deleted file mode 100644
index a46d2d2..0000000
--- a/mpc/extend/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,304 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, W_D, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.W_D = np.array(W_D)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D)
-
- for _ in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
-
- def update_system_model(self, A, B, W_D):
- """update system model
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- """
-
- self.A = A
- self.B = B
- self.W_D = W_D
-
- self.initialize_controller()
diff --git a/mpc/extend/traj_func.py b/mpc/extend/traj_func.py
deleted file mode 100644
index 8f5ce18..0000000
--- a/mpc/extend/traj_func.py
+++ /dev/null
@@ -1,31 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-def make_sample_traj(NUM, dt=0.01, a=30.):
- """
- make sample trajectory
- Parameters
- ------------
- NUM : int
- dt : float
- a : float
-
- Returns
- ----------
- traj_xs : list
- traj_ys : list
- """
- DELAY = 2.
- traj_xs = []
- traj_ys = []
-
- for i in range(NUM):
- traj_xs.append(i * 0.1)
- traj_ys.append(a * math.sin(dt * i / DELAY))
-
- plt.plot(traj_xs, traj_ys)
- plt.show()
-
- return traj_xs, traj_ys
-
diff --git a/nmpc/cgmres/README.md b/nmpc/cgmres/README.md
deleted file mode 100644
index a46901c..0000000
--- a/nmpc/cgmres/README.md
+++ /dev/null
@@ -1,79 +0,0 @@
-# CGMRES method of Nonlinear Model Predictive Control
-This program is about Continuous gmres method for NMPC
-Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
-By using CGMRES, we can pass the calculating step and get the optimal input quickly.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
-x_2-x_1+u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5) -
-- evaluation function
-
-
-
-- evaluation function
-
-+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau) -
-
-- **two wheeled model**
-
-- model
-
-
-
-
-- **two wheeled model**
-
-- model
-
-&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}) -
-- evaluation function
-
-
-
-- evaluation function
-
-^2&space;+&space;\int_{t_0}^{t_0&space;+&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt) -
-
-if you want to see more detail about this methods, you should go https://qiita.com/MENDY/items/4108190a579395053924.
-However, it is written in Japanese
-
-# Expected Results
-
-- example
-
-
-
-- two wheeled model
-
-- trajectory
-
-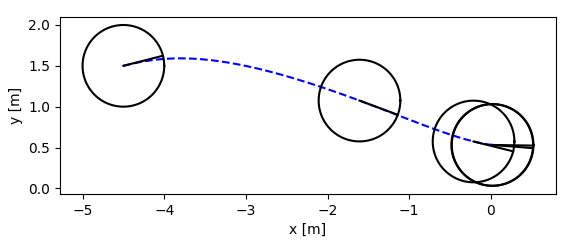
-
-- time history
-
-
-
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-```
-$ python main_two_wheeled.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
\ No newline at end of file
diff --git a/nmpc/cgmres/main_example.py b/nmpc/cgmres/main_example.py
deleted file mode 100644
index 696742c..0000000
--- a/nmpc/cgmres/main_example.py
+++ /dev/null
@@ -1,645 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(self.x_1)
- self.history_x_2.append(self.x_2)
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
- None
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = [x_1]
- x_2s = [x_2]
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s.append(temp_x_1)
- x_2s.append(temp_x_2)
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = [x_1s[-1]]
- lam_2s = [x_2s[-1]]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[0] ,lam_2s[0], us[i], dt)
- lam_1s.insert(0, temp_lam_1)
- lam_2s.insert(0, temp_lam_2)
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-class NMPCController_with_CGMRES():
- """
- Attributes
- ------------
- zeta : float
- gain of optimal answer stability
- ht : float
- update value of NMPC this should be decided by zeta
- tf : float
- predict time
- alpha : float
- gain of predict time
- N : int
- predicte step, discritize value
- threshold : float
- cgmres's threshold value
- input_num : int
- system input length, this should include dummy u and constraint variables
- max_iteration : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.zeta = 100. # 安定化ゲイン
- self.ht = 0.01 # 差分近似の幅
- self.tf = 1. # 最終時間
- self.alpha = 0.5 # 時間の上昇ゲイン
- self.N = 10 # 分割数
- self.threshold = 0.001 # break値
-
- self.input_num = 3 # dummy, 制約条件に対するuにも合わせた入力の数
- self.max_iteration = self.input_num * self.N
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros(self.N)
- self.dummy_us = np.ones(self.N) * 0.49
- self.raws = np.ones(self.N) * 0.011
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = self.tf * (1. - np.exp(-self.alpha * time)) / float(self.N)
-
- # x_dot
- x_1_dot = self.simulator.func_x_1(x_1, x_2, self.us[0])
- x_2_dot = self.simulator.func_x_2(x_1, x_2, self.us[0])
-
- dx_1 = x_1_dot * self.ht
- dx_2 = x_2_dot * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us, self.N, dt)
-
- # Fxt
- Fxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- # F
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- right = -self.zeta * F - ((Fxt - F) / self.ht)
-
- du = self.us * self.ht
- ddummy_u = self.dummy_us * self.ht
- draw = self.raws * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us + du, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us + du, self.dummy_us + ddummy_u,
- self.raws + draw, self.N, dt)
-
- left = ((Fuxt - Fxt) / self.ht)
-
- # calculationg cgmres
- r0 = right - left
- r0_norm = np.linalg.norm(r0)
-
- vs = np.zeros((self.max_iteration, self.max_iteration + 1)) # 数×iterarion回数
-
- vs[:, 0] = r0 / r0_norm # 最初の基底を算出
-
- hs = np.zeros((self.max_iteration + 1, self.max_iteration + 1))
-
- e = np.zeros((self.max_iteration + 1, 1)) # in this case the state is 3(u and dummy_u)
- e[0] = 1.
-
- for i in range(self.max_iteration):
- du = vs[::3, i] * self.ht
- ddummy_u = vs[1::3, i] * self.ht
- draw = vs[2::3, i] * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us + du, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us + du, self.dummy_us + ddummy_u,
- self.raws + draw, self.N, dt)
-
- Av = (( Fuxt - Fxt) / self.ht)
-
- sum_Av = np.zeros(self.max_iteration)
-
- for j in range(i + 1): # グラムシュミットの直交化法です、和を取って差分を取って算出します
- hs[j, i] = np.dot(Av, vs[:, j])
- sum_Av = sum_Av + hs[j, i] * vs[:, j]
-
- v_est = Av - sum_Av
-
- hs[i+1, i] = np.linalg.norm(v_est)
-
- vs[:, i+1] = v_est / hs[i+1, i]
-
- inv_hs = np.linalg.pinv(hs[:i+1, :i]) # この辺は教科書(実時間の方)にのっています
- ys = np.dot(inv_hs, r0_norm * e[:i+1])
-
- judge_value = r0_norm * e[:i+1] - np.dot(hs[:i+1, :i], ys[:i])
-
- if np.linalg.norm(judge_value) < self.threshold or i == self.max_iteration-1:
- update_value = np.dot(vs[:, :i-1], ys_pre[:i-1]).flatten()
- du_new = du + update_value[::3]
- ddummy_u_new = ddummy_u + update_value[1::3]
- draw_new = draw + update_value[2::3]
- break
-
- ys_pre = ys
-
- # update
- self.us += du_new * self.ht
- self.dummy_us += ddummy_u_new * self.ht
- self.raws += draw_new * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- print("check F = {0}".format(np.linalg.norm(F)))
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, us, dummy_us, raws, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = []
-
- for i in range(N):
- F.append(us[i] + lam_2s[i] + 2. * raws[i] * us[i])
- F.append(-0.01 + 2. * raws[i] * dummy_us[i])
- F.append(us[i]**2 + dummy_us[i]**2 - 0.5**2)
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCController_with_CGMRES()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
-
-
-
diff --git a/nmpc/cgmres/main_two_wheeled.py b/nmpc/cgmres/main_two_wheeled.py
deleted file mode 100644
index febf11d..0000000
--- a/nmpc/cgmres/main_two_wheeled.py
+++ /dev/null
@@ -1,893 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0., init_x_3=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- init_x_3 : float, optional
- initial value of x_3, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.x_3 = init_x_3
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
- self.history_x_3 = [init_x_3]
-
- def update_state(self, u_1, u_2, dt=0.01):
- """
- Palameters
- ------------
- u_1 : float
- input of system in some cases this means the reference, u_velocity
- u_2 : float
- input of system in some cases this means the reference, u_omega
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, self.x_3, u_1, u_2)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., self.x_3 + k0[2]/2., u_1, u_2)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., self.x_3 + k1[2]/2., u_1, u_2)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], self.x_3 + k2[2], u_1, u_2)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.x_3 += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- self.history_x_1.append(self.x_1)
- self.history_x_2.append(self.x_2)
- self.history_x_3.append(self.x_3)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
- None
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, x_3, u_1s, u_2s, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_3s, lam_3s for N steps
- """
- x_1s, x_2s, x_3s = self._calc_predict_states(x_1, x_2, x_3, u_1s, u_2s, N, dt) # by usin state equation
- lam_1s, lam_2s, lam_3s = self._calc_adjoint_states(x_1s, x_2s, x_3s, u_1s, u_2s, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s
-
- def _calc_predict_states(self, x_1, x_2, x_3, u_1s, u_2s, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- """
- # initial state
- x_1s = [x_1]
- x_2s = [x_2]
- x_3s = [x_3]
-
- for i in range(N):
- temp_x_1, temp_x_2, temp_x_3 = self._predict_state_with_oylar(x_1s[i], x_2s[i], x_3s[i], u_1s[i], u_2s[i], dt)
- x_1s.append(temp_x_1)
- x_2s.append(temp_x_2)
- x_3s.append(temp_x_3)
-
- return x_1s, x_2s, x_3s
-
- def _calc_adjoint_states(self, x_1s, x_2s, x_3s, u_1s, u_2s, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = [x_1s[-1]]
- lam_2s = [x_2s[-1]]
- lam_3s = [x_3s[-1]]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2, temp_lam_3 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], x_3s[i], lam_1s[0] ,lam_2s[0], lam_3s[0], u_1s[i], u_2s[i], dt)
- lam_1s.insert(0, temp_lam_1)
- lam_2s.insert(0, temp_lam_2)
- lam_3s.insert(0, temp_lam_3)
-
- return lam_1s, lam_2s, lam_3s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, x_3, u_1, u_2, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- x_3 : float
- system state
- u_1 : float
- system input
- u_2 : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- next_x_3 : float
- next state, x_3 calculated by using state equation
- """
- k0 = [0. for _ in range(3)]
-
- functions = [self.func_x_1, self.func_x_2, self.func_x_3]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, x_3, u_1, u_2)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
- next_x_3 = x_3 + k0[2]
-
- return next_x_1, next_x_2, next_x_3
-
- def func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, x_3, lam_1, lam_2, lam_3, u_1, u_2, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- x_3 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- lam_3 : float
- adjoint state
- u_1 : float
- system input
- u_2 : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- pre_lam_3 : float
- pre, 1 step before lam_3 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(3)]
-
- functions = [self._func_lam_1, self._func_lam_2, self._func_lam_3]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, x_3, lam_1, lam_2, lam_3, u_1, u_2)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
- pre_lam_3 = lam_3 + k0[2]
-
- return pre_lam_1, pre_lam_2, pre_lam_3
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = 0.
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = 0.
- return y_dot
-
- def _func_lam_3(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_3}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_3}
- """
- y_dot = - y_4 * math.sin(y_3) * u_1 + y_5 * math.cos(y_3) * u_1
- return y_dot
-
-class NMPCController_with_CGMRES():
- """
- Attributes
- ------------
- zeta : float
- gain of optimal answer stability
- ht : float
- update value of NMPC this should be decided by zeta
- tf : float
- predict time
- alpha : float
- gain of predict time
- N : int
- predicte step, discritize value
- threshold : float
- cgmres's threshold value
- input_num : int
- system input length, this should include dummy u and constraint variables
- max_iteration : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- dummy_u_1s : list of float
- estimated dummy input
- dummy_u_2s : list of float
- estimated dummy input
- raw_1s : list of float
- estimated constraint variable
- raw_2s : list of float
- estimated constraint variable
- history_u_1 : list of float
- time history of actual system input
- history_u_2 : list of float
- time history of actual system input
- history_dummy_u_1 : list of float
- time history of actual dummy u_1
- history_dummy_u_2 : list of float
- time history of actual dummy u_2
- history_raw_1 : list of float
- time history of actual raw_1
- history_raw_2 : list of float
- time history of actual raw_2
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.zeta = 100. # 安定化ゲイン
- self.ht = 0.01 # 差分近似の幅
- self.tf = 1. # 最終時間
- self.alpha = 0.5 # 時間の上昇ゲイン
- self.N = 10 # 分割数
- self.threshold = 0.001 # break値
-
- self.input_num = 6 # dummy, 制約条件に対するuにも合わせた入力の数
- self.max_iteration = self.input_num * self.N
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.u_1s = np.ones(self.N) * 1.
- self.u_2s = np.ones(self.N) * 0.1
- self.dummy_u_1s = np.ones(self.N) * 0.1
- self.dummy_u_2s = np.ones(self.N) * 2.5
- self.raw_1s = np.ones(self.N) * 0.8
- self.raw_2s = np.ones(self.N) * 0.8
-
- # for fig
- self.history_u_1 = []
- self.history_u_2 = []
- self.history_dummy_u_1 = []
- self.history_dummy_u_2 = []
- self.history_raw_1 = []
- self.history_raw_2 = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, x_3, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = self.tf * (1. - np.exp(-self.alpha * time)) / float(self.N)
-
- # x_dot
- x_1_dot = self.simulator.func_x_1(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
- x_2_dot = self.simulator.func_x_2(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
- x_3_dot = self.simulator.func_x_3(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
-
- dx_1 = x_1_dot * self.ht
- dx_2 = x_2_dot * self.ht
- dx_3 = x_3_dot * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s, self.u_2s, self.N, dt)
-
- # Fxt
- Fxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- # F
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, x_3, self.u_1s, self.u_2s, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- right = -self.zeta * F - ((Fxt - F) / self.ht)
-
- du_1 = self.u_1s * self.ht
- du_2 = self.u_2s * self.ht
- ddummy_u_1 = self.dummy_u_1s * self.ht
- ddummy_u_2 = self.dummy_u_2s * self.ht
- draw_1 = self.raw_1s * self.ht
- draw_2 = self.raw_2s * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s + du_1, self.u_2s + du_2, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s + du_1, self.u_2s + du_2, self.dummy_u_1s + ddummy_u_1, self.dummy_u_2s + ddummy_u_2,
- self.raw_1s + draw_1, self.raw_2s + draw_2, self.N, dt)
-
- left = ((Fuxt - Fxt) / self.ht)
-
- # calculationg cgmres
- r0 = right - left
- r0_norm = np.linalg.norm(r0)
-
- vs = np.zeros((self.max_iteration, self.max_iteration + 1)) # 数×iterarion回数
-
- vs[:, 0] = r0 / r0_norm # 最初の基底を算出
-
- hs = np.zeros((self.max_iteration + 1, self.max_iteration + 1))
-
- e = np.zeros((self.max_iteration + 1, 1)) # in this case the state is 3(u and dummy_u)
- e[0] = 1.
-
- for i in range(self.max_iteration):
- du_1 = vs[::self.input_num, i] * self.ht
- du_2 = vs[1::self.input_num, i] * self.ht
- ddummy_u_1 = vs[2::self.input_num, i] * self.ht
- ddummy_u_2 = vs[3::self.input_num, i] * self.ht
- draw_1 = vs[4::self.input_num, i] * self.ht
- draw_2 = vs[5::self.input_num, i] * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s + du_1, self.u_2s + du_2, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s + du_1, self.u_2s + du_2, self.dummy_u_1s + ddummy_u_1, self.dummy_u_2s + ddummy_u_2,
- self.raw_1s + draw_1, self.raw_2s + draw_2, self.N, dt)
-
- Av = (( Fuxt - Fxt) / self.ht)
-
- sum_Av = np.zeros(self.max_iteration)
-
- for j in range(i + 1): # グラムシュミットの直交化法です、和を取って差分を取って算出します
- hs[j, i] = np.dot(Av, vs[:, j])
- sum_Av = sum_Av + hs[j, i] * vs[:, j]
-
- v_est = Av - sum_Av
-
- hs[i+1, i] = np.linalg.norm(v_est)
-
- vs[:, i+1] = v_est / hs[i+1, i]
-
- inv_hs = np.linalg.pinv(hs[:i+1, :i]) # この辺は教科書(実時間の方)にのっています
- ys = np.dot(inv_hs, r0_norm * e[:i+1])
-
- judge_value = r0_norm * e[:i+1] - np.dot(hs[:i+1, :i], ys[:i])
-
- if np.linalg.norm(judge_value) < self.threshold or i == self.max_iteration-1:
- update_value = np.dot(vs[:, :i-1], ys_pre[:i-1]).flatten()
- du_1_new = du_1 + update_value[::self.input_num]
- du_2_new = du_2 + update_value[1::self.input_num]
- ddummy_u_1_new = ddummy_u_1 + update_value[2::self.input_num]
- ddummy_u_2_new = ddummy_u_2 + update_value[3::self.input_num]
- draw_1_new = draw_1 + update_value[4::self.input_num]
- draw_2_new = draw_2 + update_value[5::self.input_num]
- break
-
- ys_pre = ys
-
- # update
- self.u_1s += du_1_new * self.ht
- self.u_2s += du_2_new * self.ht
- self.dummy_u_1s += ddummy_u_1_new * self.ht
- self.dummy_u_2s += ddummy_u_2_new * self.ht
- self.raw_1s += draw_1_new * self.ht
- self.raw_2s += draw_2_new * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, x_3, self.u_1s, self.u_2s, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- print("check F = {0}".format(np.linalg.norm(F)))
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u_1.append(self.u_1s[0])
- self.history_u_2.append(self.u_2s[0])
- self.history_dummy_u_1.append(self.dummy_u_1s[0])
- self.history_dummy_u_2.append(self.dummy_u_2s[0])
- self.history_raw_1.append(self.raw_1s[0])
- self.history_raw_2.append(self.raw_2s[0])
-
- return self.u_1s, self.u_2s
-
- def _calc_f(self, x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, u_1s, u_2s, dummy_u_1s, dummy_u_2s, raw_1s, raw_2s, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_2s, lam_3s for N steps
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- dummy_u_1s : list of float
- estimated dummy input
- dummy_u_2s : list of float
- estimated dummy input
- raw_1s : list of float
- estimated constraint variable
- raw_2s : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = []
-
- for i in range(N):
- F.append(u_1s[i] + lam_1s[i] * math.cos(x_3s[i]) + lam_2s[i] * math.sin(x_3s[i]) + 2 * raw_1s[i] * u_1s[i])
- F.append(u_2s[i] + lam_3s[i] + 2 * raw_2s[i] * u_2s[i])
- F.append(-0.01 + 2. * raw_1s[i] * dummy_u_1s[i])
- F.append(-0.01 + 2. * raw_2s[i] * dummy_u_2s[i])
- F.append(u_1s[i]**2 + dummy_u_1s[i]**2 - 1.**2)
- F.append(u_2s[i]**2 + dummy_u_2s[i]**2 - 1.5**2)
-
- return np.array(F)
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 15.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = TwoWheeledSystem(init_x_1=-4.5, init_x_2=1.5, init_x_3=0.25)
-
- # controller
- controller = NMPCController_with_CGMRES()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- x_3 = plant_system.x_3
- # make input
- u_1s, u_2s = controller.calc_input(x_1, x_2, x_3, time)
- # update state
- plant_system.update_state(u_1s[0], u_2s[0])
-
- # figure
- # time history
- fig_p = plt.figure()
- fig_u = plt.figure()
- fig_f = plt.figure()
-
- # traj
- fig_t = plt.figure()
- fig_traj = fig_t.add_subplot(111)
- fig_traj.set_aspect('equal')
-
- x_1_fig = fig_p.add_subplot(311)
- x_2_fig = fig_p.add_subplot(312)
- x_3_fig = fig_p.add_subplot(313)
-
- u_1_fig = fig_u.add_subplot(411)
- u_2_fig = fig_u.add_subplot(412)
- dummy_1_fig = fig_u.add_subplot(413)
- dummy_2_fig = fig_u.add_subplot(414)
-
- raw_1_fig = fig_f.add_subplot(311)
- raw_2_fig = fig_f.add_subplot(312)
- f_fig = fig_f.add_subplot(313)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- x_3_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_3)
- x_3_fig.set_xlabel("time [s]")
- x_3_fig.set_ylabel("x_3")
-
- u_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u_1)
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_v")
-
- u_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u_2)
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_omega")
-
- dummy_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u_1)
- dummy_1_fig.set_xlabel("time [s]")
- dummy_1_fig.set_ylabel("dummy u_1")
-
- dummy_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u_2)
- dummy_2_fig.set_xlabel("time [s]")
- dummy_2_fig.set_ylabel("dummy u_2")
-
- raw_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw_1)
- raw_1_fig.set_xlabel("time [s]")
- raw_1_fig.set_ylabel("raw_1")
-
- raw_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw_2)
- raw_2_fig.set_xlabel("time [s]")
- raw_2_fig.set_ylabel("raw_2")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig_traj.plot(plant_system.history_x_1, plant_system.history_x_2, color="b", linestyle="dashed")
- fig_traj.set_xlabel("x [m]")
- fig_traj.set_ylabel("y [m]")
-
- write_obj_num = 5
- count_num = int(iteration_num / write_obj_num)
-
- for i in np.arange(0, iteration_num, count_num):
- obj_xs, obj_ys, obj_line_xs, obj_line_ys = circle_make_with_angles(plant_system.history_x_1[i], plant_system.history_x_2[i], 0.5, plant_system.history_x_3[i])
- fig_traj.plot(obj_xs, obj_ys, color="k")
- fig_traj.plot(obj_line_xs, obj_line_ys, color="k")
-
- fig_p.tight_layout()
- fig_u.tight_layout()
- fig_f.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
-
-
-
diff --git a/nmpc/newton/README.md b/nmpc/newton/README.md
deleted file mode 100644
index 94f24c9..0000000
--- a/nmpc/newton/README.md
+++ /dev/null
@@ -1,65 +0,0 @@
-# Newton method of Nonlinear Model Predictive Control
-This program is about NMPC with newton method.
-Usually we have to calculate the partial differential of optimal matrix.
-In this program, in stead of using any paticular methods to calculate the partial differential of optimal matrix, I used numerical differentiation.
-Therefore, I believe that it easy to understand and extend your model.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
-
-
-
-if you want to see more detail about this methods, you should go https://qiita.com/MENDY/items/4108190a579395053924.
-However, it is written in Japanese
-
-# Expected Results
-
-- example
-
-
-
-- two wheeled model
-
-- trajectory
-
-
-
-- time history
-
-
-
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-```
-$ python main_two_wheeled.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
\ No newline at end of file
diff --git a/nmpc/cgmres/main_example.py b/nmpc/cgmres/main_example.py
deleted file mode 100644
index 696742c..0000000
--- a/nmpc/cgmres/main_example.py
+++ /dev/null
@@ -1,645 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(self.x_1)
- self.history_x_2.append(self.x_2)
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
- None
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = [x_1]
- x_2s = [x_2]
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s.append(temp_x_1)
- x_2s.append(temp_x_2)
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = [x_1s[-1]]
- lam_2s = [x_2s[-1]]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[0] ,lam_2s[0], us[i], dt)
- lam_1s.insert(0, temp_lam_1)
- lam_2s.insert(0, temp_lam_2)
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-class NMPCController_with_CGMRES():
- """
- Attributes
- ------------
- zeta : float
- gain of optimal answer stability
- ht : float
- update value of NMPC this should be decided by zeta
- tf : float
- predict time
- alpha : float
- gain of predict time
- N : int
- predicte step, discritize value
- threshold : float
- cgmres's threshold value
- input_num : int
- system input length, this should include dummy u and constraint variables
- max_iteration : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.zeta = 100. # 安定化ゲイン
- self.ht = 0.01 # 差分近似の幅
- self.tf = 1. # 最終時間
- self.alpha = 0.5 # 時間の上昇ゲイン
- self.N = 10 # 分割数
- self.threshold = 0.001 # break値
-
- self.input_num = 3 # dummy, 制約条件に対するuにも合わせた入力の数
- self.max_iteration = self.input_num * self.N
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros(self.N)
- self.dummy_us = np.ones(self.N) * 0.49
- self.raws = np.ones(self.N) * 0.011
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = self.tf * (1. - np.exp(-self.alpha * time)) / float(self.N)
-
- # x_dot
- x_1_dot = self.simulator.func_x_1(x_1, x_2, self.us[0])
- x_2_dot = self.simulator.func_x_2(x_1, x_2, self.us[0])
-
- dx_1 = x_1_dot * self.ht
- dx_2 = x_2_dot * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us, self.N, dt)
-
- # Fxt
- Fxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- # F
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- right = -self.zeta * F - ((Fxt - F) / self.ht)
-
- du = self.us * self.ht
- ddummy_u = self.dummy_us * self.ht
- draw = self.raws * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us + du, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us + du, self.dummy_us + ddummy_u,
- self.raws + draw, self.N, dt)
-
- left = ((Fuxt - Fxt) / self.ht)
-
- # calculationg cgmres
- r0 = right - left
- r0_norm = np.linalg.norm(r0)
-
- vs = np.zeros((self.max_iteration, self.max_iteration + 1)) # 数×iterarion回数
-
- vs[:, 0] = r0 / r0_norm # 最初の基底を算出
-
- hs = np.zeros((self.max_iteration + 1, self.max_iteration + 1))
-
- e = np.zeros((self.max_iteration + 1, 1)) # in this case the state is 3(u and dummy_u)
- e[0] = 1.
-
- for i in range(self.max_iteration):
- du = vs[::3, i] * self.ht
- ddummy_u = vs[1::3, i] * self.ht
- draw = vs[2::3, i] * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, self.us + du, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us + du, self.dummy_us + ddummy_u,
- self.raws + draw, self.N, dt)
-
- Av = (( Fuxt - Fxt) / self.ht)
-
- sum_Av = np.zeros(self.max_iteration)
-
- for j in range(i + 1): # グラムシュミットの直交化法です、和を取って差分を取って算出します
- hs[j, i] = np.dot(Av, vs[:, j])
- sum_Av = sum_Av + hs[j, i] * vs[:, j]
-
- v_est = Av - sum_Av
-
- hs[i+1, i] = np.linalg.norm(v_est)
-
- vs[:, i+1] = v_est / hs[i+1, i]
-
- inv_hs = np.linalg.pinv(hs[:i+1, :i]) # この辺は教科書(実時間の方)にのっています
- ys = np.dot(inv_hs, r0_norm * e[:i+1])
-
- judge_value = r0_norm * e[:i+1] - np.dot(hs[:i+1, :i], ys[:i])
-
- if np.linalg.norm(judge_value) < self.threshold or i == self.max_iteration-1:
- update_value = np.dot(vs[:, :i-1], ys_pre[:i-1]).flatten()
- du_new = du + update_value[::3]
- ddummy_u_new = ddummy_u + update_value[1::3]
- draw_new = draw + update_value[2::3]
- break
-
- ys_pre = ys
-
- # update
- self.us += du_new * self.ht
- self.dummy_us += ddummy_u_new * self.ht
- self.raws += draw_new * self.ht
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, self.us, self.dummy_us,
- self.raws, self.N, dt)
-
- print("check F = {0}".format(np.linalg.norm(F)))
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, us, dummy_us, raws, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = []
-
- for i in range(N):
- F.append(us[i] + lam_2s[i] + 2. * raws[i] * us[i])
- F.append(-0.01 + 2. * raws[i] * dummy_us[i])
- F.append(us[i]**2 + dummy_us[i]**2 - 0.5**2)
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCController_with_CGMRES()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
-
-
-
diff --git a/nmpc/cgmres/main_two_wheeled.py b/nmpc/cgmres/main_two_wheeled.py
deleted file mode 100644
index febf11d..0000000
--- a/nmpc/cgmres/main_two_wheeled.py
+++ /dev/null
@@ -1,893 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0., init_x_3=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- init_x_3 : float, optional
- initial value of x_3, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.x_3 = init_x_3
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
- self.history_x_3 = [init_x_3]
-
- def update_state(self, u_1, u_2, dt=0.01):
- """
- Palameters
- ------------
- u_1 : float
- input of system in some cases this means the reference, u_velocity
- u_2 : float
- input of system in some cases this means the reference, u_omega
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, self.x_3, u_1, u_2)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., self.x_3 + k0[2]/2., u_1, u_2)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., self.x_3 + k1[2]/2., u_1, u_2)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], self.x_3 + k2[2], u_1, u_2)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.x_3 += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- self.history_x_1.append(self.x_1)
- self.history_x_2.append(self.x_2)
- self.history_x_3.append(self.x_3)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
- None
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, x_3, u_1s, u_2s, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_3s, lam_3s for N steps
- """
- x_1s, x_2s, x_3s = self._calc_predict_states(x_1, x_2, x_3, u_1s, u_2s, N, dt) # by usin state equation
- lam_1s, lam_2s, lam_3s = self._calc_adjoint_states(x_1s, x_2s, x_3s, u_1s, u_2s, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s
-
- def _calc_predict_states(self, x_1, x_2, x_3, u_1s, u_2s, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- """
- # initial state
- x_1s = [x_1]
- x_2s = [x_2]
- x_3s = [x_3]
-
- for i in range(N):
- temp_x_1, temp_x_2, temp_x_3 = self._predict_state_with_oylar(x_1s[i], x_2s[i], x_3s[i], u_1s[i], u_2s[i], dt)
- x_1s.append(temp_x_1)
- x_2s.append(temp_x_2)
- x_3s.append(temp_x_3)
-
- return x_1s, x_2s, x_3s
-
- def _calc_adjoint_states(self, x_1s, x_2s, x_3s, u_1s, u_2s, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- u_1s : list of float
- estimated optimal input Us for N steps
- u_2s : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = [x_1s[-1]]
- lam_2s = [x_2s[-1]]
- lam_3s = [x_3s[-1]]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2, temp_lam_3 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], x_3s[i], lam_1s[0] ,lam_2s[0], lam_3s[0], u_1s[i], u_2s[i], dt)
- lam_1s.insert(0, temp_lam_1)
- lam_2s.insert(0, temp_lam_2)
- lam_3s.insert(0, temp_lam_3)
-
- return lam_1s, lam_2s, lam_3s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, x_3, u_1, u_2, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- x_3 : float
- system state
- u_1 : float
- system input
- u_2 : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- next_x_3 : float
- next state, x_3 calculated by using state equation
- """
- k0 = [0. for _ in range(3)]
-
- functions = [self.func_x_1, self.func_x_2, self.func_x_3]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, x_3, u_1, u_2)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
- next_x_3 = x_3 + k0[2]
-
- return next_x_1, next_x_2, next_x_3
-
- def func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, x_3, lam_1, lam_2, lam_3, u_1, u_2, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- x_3 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- lam_3 : float
- adjoint state
- u_1 : float
- system input
- u_2 : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- pre_lam_3 : float
- pre, 1 step before lam_3 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(3)]
-
- functions = [self._func_lam_1, self._func_lam_2, self._func_lam_3]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, x_3, lam_1, lam_2, lam_3, u_1, u_2)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
- pre_lam_3 = lam_3 + k0[2]
-
- return pre_lam_1, pre_lam_2, pre_lam_3
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = 0.
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = 0.
- return y_dot
-
- def _func_lam_3(self, y_1, y_2, y_3, y_4, y_5, y_6, u_1, u_2):
- """calculating -\dot{lam_3}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means x_3
- y_4 : float
- means lam_1
- y_5 : float
- means lam_2
- y_6 : float
- means lam_3
- u_1 : float
- means system input
- u_2 : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_3}
- """
- y_dot = - y_4 * math.sin(y_3) * u_1 + y_5 * math.cos(y_3) * u_1
- return y_dot
-
-class NMPCController_with_CGMRES():
- """
- Attributes
- ------------
- zeta : float
- gain of optimal answer stability
- ht : float
- update value of NMPC this should be decided by zeta
- tf : float
- predict time
- alpha : float
- gain of predict time
- N : int
- predicte step, discritize value
- threshold : float
- cgmres's threshold value
- input_num : int
- system input length, this should include dummy u and constraint variables
- max_iteration : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- dummy_u_1s : list of float
- estimated dummy input
- dummy_u_2s : list of float
- estimated dummy input
- raw_1s : list of float
- estimated constraint variable
- raw_2s : list of float
- estimated constraint variable
- history_u_1 : list of float
- time history of actual system input
- history_u_2 : list of float
- time history of actual system input
- history_dummy_u_1 : list of float
- time history of actual dummy u_1
- history_dummy_u_2 : list of float
- time history of actual dummy u_2
- history_raw_1 : list of float
- time history of actual raw_1
- history_raw_2 : list of float
- time history of actual raw_2
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.zeta = 100. # 安定化ゲイン
- self.ht = 0.01 # 差分近似の幅
- self.tf = 1. # 最終時間
- self.alpha = 0.5 # 時間の上昇ゲイン
- self.N = 10 # 分割数
- self.threshold = 0.001 # break値
-
- self.input_num = 6 # dummy, 制約条件に対するuにも合わせた入力の数
- self.max_iteration = self.input_num * self.N
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.u_1s = np.ones(self.N) * 1.
- self.u_2s = np.ones(self.N) * 0.1
- self.dummy_u_1s = np.ones(self.N) * 0.1
- self.dummy_u_2s = np.ones(self.N) * 2.5
- self.raw_1s = np.ones(self.N) * 0.8
- self.raw_2s = np.ones(self.N) * 0.8
-
- # for fig
- self.history_u_1 = []
- self.history_u_2 = []
- self.history_dummy_u_1 = []
- self.history_dummy_u_2 = []
- self.history_raw_1 = []
- self.history_raw_2 = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, x_3, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- x_3 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = self.tf * (1. - np.exp(-self.alpha * time)) / float(self.N)
-
- # x_dot
- x_1_dot = self.simulator.func_x_1(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
- x_2_dot = self.simulator.func_x_2(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
- x_3_dot = self.simulator.func_x_3(x_1, x_2, x_3, self.u_1s[0], self.u_2s[0])
-
- dx_1 = x_1_dot * self.ht
- dx_2 = x_2_dot * self.ht
- dx_3 = x_3_dot * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s, self.u_2s, self.N, dt)
-
- # Fxt
- Fxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- # F
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, x_3, self.u_1s, self.u_2s, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- right = -self.zeta * F - ((Fxt - F) / self.ht)
-
- du_1 = self.u_1s * self.ht
- du_2 = self.u_2s * self.ht
- ddummy_u_1 = self.dummy_u_1s * self.ht
- ddummy_u_2 = self.dummy_u_2s * self.ht
- draw_1 = self.raw_1s * self.ht
- draw_2 = self.raw_2s * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s + du_1, self.u_2s + du_2, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s + du_1, self.u_2s + du_2, self.dummy_u_1s + ddummy_u_1, self.dummy_u_2s + ddummy_u_2,
- self.raw_1s + draw_1, self.raw_2s + draw_2, self.N, dt)
-
- left = ((Fuxt - Fxt) / self.ht)
-
- # calculationg cgmres
- r0 = right - left
- r0_norm = np.linalg.norm(r0)
-
- vs = np.zeros((self.max_iteration, self.max_iteration + 1)) # 数×iterarion回数
-
- vs[:, 0] = r0 / r0_norm # 最初の基底を算出
-
- hs = np.zeros((self.max_iteration + 1, self.max_iteration + 1))
-
- e = np.zeros((self.max_iteration + 1, 1)) # in this case the state is 3(u and dummy_u)
- e[0] = 1.
-
- for i in range(self.max_iteration):
- du_1 = vs[::self.input_num, i] * self.ht
- du_2 = vs[1::self.input_num, i] * self.ht
- ddummy_u_1 = vs[2::self.input_num, i] * self.ht
- ddummy_u_2 = vs[3::self.input_num, i] * self.ht
- draw_1 = vs[4::self.input_num, i] * self.ht
- draw_2 = vs[5::self.input_num, i] * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1 + dx_1, x_2 + dx_2, x_3 + dx_3, self.u_1s + du_1, self.u_2s + du_2, self.N, dt)
-
- Fuxt = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s + du_1, self.u_2s + du_2, self.dummy_u_1s + ddummy_u_1, self.dummy_u_2s + ddummy_u_2,
- self.raw_1s + draw_1, self.raw_2s + draw_2, self.N, dt)
-
- Av = (( Fuxt - Fxt) / self.ht)
-
- sum_Av = np.zeros(self.max_iteration)
-
- for j in range(i + 1): # グラムシュミットの直交化法です、和を取って差分を取って算出します
- hs[j, i] = np.dot(Av, vs[:, j])
- sum_Av = sum_Av + hs[j, i] * vs[:, j]
-
- v_est = Av - sum_Av
-
- hs[i+1, i] = np.linalg.norm(v_est)
-
- vs[:, i+1] = v_est / hs[i+1, i]
-
- inv_hs = np.linalg.pinv(hs[:i+1, :i]) # この辺は教科書(実時間の方)にのっています
- ys = np.dot(inv_hs, r0_norm * e[:i+1])
-
- judge_value = r0_norm * e[:i+1] - np.dot(hs[:i+1, :i], ys[:i])
-
- if np.linalg.norm(judge_value) < self.threshold or i == self.max_iteration-1:
- update_value = np.dot(vs[:, :i-1], ys_pre[:i-1]).flatten()
- du_1_new = du_1 + update_value[::self.input_num]
- du_2_new = du_2 + update_value[1::self.input_num]
- ddummy_u_1_new = ddummy_u_1 + update_value[2::self.input_num]
- ddummy_u_2_new = ddummy_u_2 + update_value[3::self.input_num]
- draw_1_new = draw_1 + update_value[4::self.input_num]
- draw_2_new = draw_2 + update_value[5::self.input_num]
- break
-
- ys_pre = ys
-
- # update
- self.u_1s += du_1_new * self.ht
- self.u_2s += du_2_new * self.ht
- self.dummy_u_1s += ddummy_u_1_new * self.ht
- self.dummy_u_2s += ddummy_u_2_new * self.ht
- self.raw_1s += draw_1_new * self.ht
- self.raw_2s += draw_2_new * self.ht
-
- x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, x_3, self.u_1s, self.u_2s, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, self.u_1s, self.u_2s, self.dummy_u_1s, self.dummy_u_2s,
- self.raw_1s, self.raw_2s, self.N, dt)
-
- print("check F = {0}".format(np.linalg.norm(F)))
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u_1.append(self.u_1s[0])
- self.history_u_2.append(self.u_2s[0])
- self.history_dummy_u_1.append(self.dummy_u_1s[0])
- self.history_dummy_u_2.append(self.dummy_u_2s[0])
- self.history_raw_1.append(self.raw_1s[0])
- self.history_raw_2.append(self.raw_2s[0])
-
- return self.u_1s, self.u_2s
-
- def _calc_f(self, x_1s, x_2s, x_3s, lam_1s, lam_2s, lam_3s, u_1s, u_2s, dummy_u_1s, dummy_u_2s, raw_1s, raw_2s, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- x_3s : list of float
- predicted x_3s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- lam_3s : list of float
- adjoint state of x_2s, lam_3s for N steps
- u_1s : list of float
- estimated optimal system input
- u_2s : list of float
- estimated optimal system input
- dummy_u_1s : list of float
- estimated dummy input
- dummy_u_2s : list of float
- estimated dummy input
- raw_1s : list of float
- estimated constraint variable
- raw_2s : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = []
-
- for i in range(N):
- F.append(u_1s[i] + lam_1s[i] * math.cos(x_3s[i]) + lam_2s[i] * math.sin(x_3s[i]) + 2 * raw_1s[i] * u_1s[i])
- F.append(u_2s[i] + lam_3s[i] + 2 * raw_2s[i] * u_2s[i])
- F.append(-0.01 + 2. * raw_1s[i] * dummy_u_1s[i])
- F.append(-0.01 + 2. * raw_2s[i] * dummy_u_2s[i])
- F.append(u_1s[i]**2 + dummy_u_1s[i]**2 - 1.**2)
- F.append(u_2s[i]**2 + dummy_u_2s[i]**2 - 1.5**2)
-
- return np.array(F)
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 15.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = TwoWheeledSystem(init_x_1=-4.5, init_x_2=1.5, init_x_3=0.25)
-
- # controller
- controller = NMPCController_with_CGMRES()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- x_3 = plant_system.x_3
- # make input
- u_1s, u_2s = controller.calc_input(x_1, x_2, x_3, time)
- # update state
- plant_system.update_state(u_1s[0], u_2s[0])
-
- # figure
- # time history
- fig_p = plt.figure()
- fig_u = plt.figure()
- fig_f = plt.figure()
-
- # traj
- fig_t = plt.figure()
- fig_traj = fig_t.add_subplot(111)
- fig_traj.set_aspect('equal')
-
- x_1_fig = fig_p.add_subplot(311)
- x_2_fig = fig_p.add_subplot(312)
- x_3_fig = fig_p.add_subplot(313)
-
- u_1_fig = fig_u.add_subplot(411)
- u_2_fig = fig_u.add_subplot(412)
- dummy_1_fig = fig_u.add_subplot(413)
- dummy_2_fig = fig_u.add_subplot(414)
-
- raw_1_fig = fig_f.add_subplot(311)
- raw_2_fig = fig_f.add_subplot(312)
- f_fig = fig_f.add_subplot(313)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- x_3_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_3)
- x_3_fig.set_xlabel("time [s]")
- x_3_fig.set_ylabel("x_3")
-
- u_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u_1)
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_v")
-
- u_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u_2)
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_omega")
-
- dummy_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u_1)
- dummy_1_fig.set_xlabel("time [s]")
- dummy_1_fig.set_ylabel("dummy u_1")
-
- dummy_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u_2)
- dummy_2_fig.set_xlabel("time [s]")
- dummy_2_fig.set_ylabel("dummy u_2")
-
- raw_1_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw_1)
- raw_1_fig.set_xlabel("time [s]")
- raw_1_fig.set_ylabel("raw_1")
-
- raw_2_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw_2)
- raw_2_fig.set_xlabel("time [s]")
- raw_2_fig.set_ylabel("raw_2")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig_traj.plot(plant_system.history_x_1, plant_system.history_x_2, color="b", linestyle="dashed")
- fig_traj.set_xlabel("x [m]")
- fig_traj.set_ylabel("y [m]")
-
- write_obj_num = 5
- count_num = int(iteration_num / write_obj_num)
-
- for i in np.arange(0, iteration_num, count_num):
- obj_xs, obj_ys, obj_line_xs, obj_line_ys = circle_make_with_angles(plant_system.history_x_1[i], plant_system.history_x_2[i], 0.5, plant_system.history_x_3[i])
- fig_traj.plot(obj_xs, obj_ys, color="k")
- fig_traj.plot(obj_line_xs, obj_line_ys, color="k")
-
- fig_p.tight_layout()
- fig_u.tight_layout()
- fig_f.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
-
-
-
diff --git a/nmpc/newton/README.md b/nmpc/newton/README.md
deleted file mode 100644
index 94f24c9..0000000
--- a/nmpc/newton/README.md
+++ /dev/null
@@ -1,65 +0,0 @@
-# Newton method of Nonlinear Model Predictive Control
-This program is about NMPC with newton method.
-Usually we have to calculate the partial differential of optimal matrix.
-In this program, in stead of using any paticular methods to calculate the partial differential of optimal matrix, I used numerical differentiation.
-Therefore, I believe that it easy to understand and extend your model.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
-x_2-x_1+u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5) -
-- evaluation function
-
-To consider the constraints of input u, I introduced dummy input.
-
-
-
-- evaluation function
-
-To consider the constraints of input u, I introduced dummy input.
-
-+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau) -
-
-- **two wheeled model**
-
-coming soon !
-
-# Expected Results
-
-- example
-
-
-
-
-- **two wheeled model**
-
-coming soon !
-
-# Expected Results
-
-- example
-
- -
-you can confirm that the my method could consider the constraints of input.
-
-- two wheeled model
-
-coming soon !
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-coming soon !
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
diff --git a/nmpc/newton/main_example.py b/nmpc/newton/main_example.py
deleted file mode 100644
index 4ab4a4c..0000000
--- a/nmpc/newton/main_example.py
+++ /dev/null
@@ -1,657 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(copy.deepcopy(self.x_1))
- self.history_x_2.append(copy.deepcopy(self.x_2))
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = np.zeros(N+1)
- x_2s = np.zeros(N+1)
-
- # input initial state
- x_1s[0] = x_1
- x_2s[0] = x_2
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s[i+1] = temp_x_1
- x_2s[i+1] = temp_x_2
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = np.zeros(N)
- lam_2s = np.zeros(N)
-
- # input final state
- lam_1s[-1] = x_1s[-1]
- lam_2s[-1] = x_2s[-1]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[i] ,lam_2s[i], us[i], dt)
- lam_1s[i-1] = temp_lam_1
- lam_2s[i-1] = temp_lam_2
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-
-def calc_numerical_gradient(forward_prop, grad_f, all_us, shape, input_size):
- """
- Parameters
- ------------
- forward_prop : function
- forward prop
- grad_f : function
- gradient function
- all_us : numpy.ndarray, shape(pred_len, input_size*3)
- all inputs including with dummy input
- shape : tuple
- shape of Jacobian
- input_size : int
- input size of system
-
- Returns
- ---------
- grad : numpy.ndarray, shape is the same as shape
- results of numercial gradient of the input
-
- References
- -----------
- - oreilly japan 0 から作るdeeplearning
- https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/gradient.py
- """
- h = 1e-3 # 0.01
- grad = np.zeros(shape)
- grad_idx = 0
-
- it = np.nditer(all_us, flags=['multi_index'], op_flags=['readwrite'])
- while not it.finished:
- # get index
- idx = it.multi_index
- # save and return
- tmp_val = all_us[idx]
-
- # 差分を取る
- # 上側の差分
- all_us[idx] = float(tmp_val) + h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh1 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- # 下側の差分
- all_us[idx] = float(tmp_val) - h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh2 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- grad[:, grad_idx] = ((fuh1 - fuh2) / (2.*h)).flatten() # to flat でgradに代入できるように
-
- all_us[idx] = tmp_val
- it.iternext()
- grad_idx += 1
-
- return np.array(grad)
-
-class NMPCControllerWithNewton():
- """
- Attributes
- ------------
- N : int
- predicte step, discritize value
- threshold : float
- newton's threshold value
- NUM_INPUT : int
- system input length, this should include dummy u and constraint variables
- MAX_ITERATION : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.N = 10 # time step
- self.threshold = 0.0001 # break
-
- self.NUM_ALL_INPUT = 3 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.NUM_INPUT = 1 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.Jacobian_size = self.NUM_ALL_INPUT * self.N
-
- # newton parameters
- self.MAX_ITERATION = 100
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros((self.N, self.NUM_INPUT))
- self.dummy_us = np.ones((self.N, self.NUM_INPUT)) * 0.25
- self.raws = np.ones((self.N, self.NUM_INPUT)) * 0.01
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = 0.01
-
- # concat all us, shape (pred_len, input_size)
- all_us = np.hstack((self.us, self.dummy_us, self.raws))
-
- # Newton method
- for i in range(self.MAX_ITERATION):
- # calc all state
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- # F
- F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # judge
- if np.linalg.norm(F_hat) < self.threshold:
- # print("break!!")
- break
-
- grad_f = lambda x_1s, x_2s, lam_1s, lam_2s, all_us : self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
- forward_prop_f = lambda us : self.simulator.calc_predict_and_adjoint_state(x_1, x_2, us, self.N, dt)
- grads = calc_numerical_gradient(forward_prop_f, grad_f, all_us, (self.Jacobian_size, self.Jacobian_size), self.NUM_INPUT)
-
- # make jacobian and calc inverse of it
- # grads += np.eye(self.Jacobian_size) * 1e-8
- try:
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
- except np.linalg.LinAlgError:
- print("Warning : singular matrix!!")
- grads += np.eye(self.Jacobian_size) * 1e-10 # add noise
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
-
- all_us = all_us.reshape(self.N, self.NUM_ALL_INPUT)
-
- # update
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- # final insert
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, all_us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = np.zeros((N, self.NUM_INPUT*3))
-
- us = all_us[:, :self.NUM_INPUT].flatten()
- dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT].flatten()
- raws = all_us[:, 2*self.NUM_INPUT:].flatten()
-
- for i in range(N):
- F_u = 0.5 * us[i] + lam_2s[i] + 2. * raws[i] * us[i]
- F_dummy = -0.01 + 2. * raws[i] * dummy_us[i]
- F_raw = us[i]**2 + dummy_us[i]**2 - 0.5**2
-
- F[i] = np.array([F_u, F_dummy, F_raw])
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCControllerWithNewton()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- print("iteration = {}".format(i))
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/scripts/simple_run.py b/scripts/simple_run.py
new file mode 100644
index 0000000..510e24e
--- /dev/null
+++ b/scripts/simple_run.py
@@ -0,0 +1,53 @@
+import argparse
+
+from PythonLinearNonlinearControl.helper import bool_flag, make_logger
+from PythonLinearNonlinearControl.controllers.make_controllers import make_controller
+from PythonLinearNonlinearControl.planners.make_planners import make_planner
+from PythonLinearNonlinearControl.configs.make_configs import make_config
+from PythonLinearNonlinearControl.models.make_models import make_model
+from PythonLinearNonlinearControl.envs.make_envs import make_env
+from PythonLinearNonlinearControl.runners.make_runners import make_runner
+from PythonLinearNonlinearControl.plotters.plot_func import plot_results
+
+def run(args):
+ # logger
+ make_logger(args.result_dir)
+
+ # make envs
+ env = make_env(args)
+
+ # make config
+ config = make_config(args)
+
+ # make planner
+ planner = make_planner(args, config)
+
+ # make model
+ model = make_model(args, config)
+
+ # make controller
+ controller = make_controller(args, config, model)
+
+ # make simulator
+ runner = make_runner(args)
+
+ # run experiment
+ history_x, history_u, history_g = runner.run(env, controller, planner)
+
+ # plot results
+ plot_results(args, history_x, history_u, history_g=history_g)
+
+def main():
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--controller_type", type=str, default="MPC")
+ parser.add_argument("--planner_type", type=str, default="const")
+ parser.add_argument("--env", type=str, default="FirstOrderLag")
+ parser.add_argument("--result_dir", type=str, default="./result")
+
+ args = parser.parse_args()
+
+ run(args)
+
+if __name__ == "__main__":
+ main()
\ No newline at end of file
diff --git a/setup.py b/setup.py
new file mode 100644
index 0000000..7ea6a7c
--- /dev/null
+++ b/setup.py
@@ -0,0 +1,21 @@
+from setuptools import find_packages
+from setuptools import setup
+
+install_requires = ['numpy', 'matplotlib', 'cvxopt']
+tests_require = ['pytest']
+setup_requires = ["pytest-runner"]
+
+setup(
+ name='PythonLinearNonlinearControl',
+ version='2.0',
+ description='Implementing linear and non-linear control method in python',
+ author='Shunichi Sekiguchi',
+ author_email='quick1st97of@gmail.com',
+ install_requires=install_requires,
+ url='https://github.com/Shunichi09/PythonLinearNonlinearControl',
+ license='MIT License',
+ packages=find_packages(exclude=('tests')),
+ setup_requires=setup_requires,
+ test_suite='tests',
+ tests_require=tests_require
+)
\ No newline at end of file
diff --git a/tests/__init__.py b/tests/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/__init__.py b/tests/configs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/test_first_order_lag.py b/tests/configs/test_first_order_lag.py
new file mode 100644
index 0000000..a013fac
--- /dev/null
+++ b/tests/configs/test_first_order_lag.py
@@ -0,0 +1,34 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.configs.first_order_lag \
+ import FirstOrderLagConfigModule
+
+class TestCalcCost():
+ def test_calc_costs(self):
+ # make config
+ config = FirstOrderLagConfigModule()
+ # set
+ pred_len = 5
+ state_size = 4
+ input_size = 2
+ pop_size = 2
+ pred_xs = np.ones((pop_size, pred_len, state_size))
+ g_xs = np.ones((pop_size, pred_len, state_size)) * 0.5
+ input_samples = np.ones((pop_size, pred_len, input_size)) * 0.5
+
+ costs = config.input_cost_fn(input_samples)
+ expected_costs = np.ones((pop_size, pred_len, input_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.R))
+
+ costs = config.state_cost_fn(pred_xs, g_xs)
+ expected_costs = np.ones((pop_size, pred_len, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Q))
+
+ costs = config.terminal_state_cost_fn(pred_xs[:, -1, :],\
+ g_xs[:, -1, :])
+ expected_costs = np.ones((pop_size, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Sf))
\ No newline at end of file
diff --git a/tests/models/__init__.py b/tests/models/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/models/test_model.py b/tests/models/test_model.py
new file mode 100644
index 0000000..e11a439
--- /dev/null
+++ b/tests/models/test_model.py
@@ -0,0 +1,53 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.models.model import LinearModel
+
+class TestLinearModel():
+ """
+ """
+ def test_predict(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ assert pred_xs == pytest.approx(np.array([[0.5, 0.5], [0.75, 1.3]]))
+
+ def test_alltogether(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ u = np.tile(u, (1, 1, 1))
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)[0]
+
+ assert pred_xs_alltogether == pytest.approx(pred_xs)
+
+ def test_alltogether_val(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.stack((np.ones((1, 1)), np.ones((1, 1))*0.5), axis=0)
+
+ linear_model = LinearModel(A, B)
+
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)
+
+ expected_val = np.array([[[0.5, 0.5], [0.75, 1.3]],
+ [[0.5, 0.5], [0.65, 1.05]]])
+
+ assert pred_xs_alltogether == pytest.approx(expected_val)
\ No newline at end of file
-
-you can confirm that the my method could consider the constraints of input.
-
-- two wheeled model
-
-coming soon !
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-coming soon !
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
diff --git a/nmpc/newton/main_example.py b/nmpc/newton/main_example.py
deleted file mode 100644
index 4ab4a4c..0000000
--- a/nmpc/newton/main_example.py
+++ /dev/null
@@ -1,657 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(copy.deepcopy(self.x_1))
- self.history_x_2.append(copy.deepcopy(self.x_2))
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = np.zeros(N+1)
- x_2s = np.zeros(N+1)
-
- # input initial state
- x_1s[0] = x_1
- x_2s[0] = x_2
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s[i+1] = temp_x_1
- x_2s[i+1] = temp_x_2
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = np.zeros(N)
- lam_2s = np.zeros(N)
-
- # input final state
- lam_1s[-1] = x_1s[-1]
- lam_2s[-1] = x_2s[-1]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[i] ,lam_2s[i], us[i], dt)
- lam_1s[i-1] = temp_lam_1
- lam_2s[i-1] = temp_lam_2
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-
-def calc_numerical_gradient(forward_prop, grad_f, all_us, shape, input_size):
- """
- Parameters
- ------------
- forward_prop : function
- forward prop
- grad_f : function
- gradient function
- all_us : numpy.ndarray, shape(pred_len, input_size*3)
- all inputs including with dummy input
- shape : tuple
- shape of Jacobian
- input_size : int
- input size of system
-
- Returns
- ---------
- grad : numpy.ndarray, shape is the same as shape
- results of numercial gradient of the input
-
- References
- -----------
- - oreilly japan 0 から作るdeeplearning
- https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/gradient.py
- """
- h = 1e-3 # 0.01
- grad = np.zeros(shape)
- grad_idx = 0
-
- it = np.nditer(all_us, flags=['multi_index'], op_flags=['readwrite'])
- while not it.finished:
- # get index
- idx = it.multi_index
- # save and return
- tmp_val = all_us[idx]
-
- # 差分を取る
- # 上側の差分
- all_us[idx] = float(tmp_val) + h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh1 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- # 下側の差分
- all_us[idx] = float(tmp_val) - h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh2 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- grad[:, grad_idx] = ((fuh1 - fuh2) / (2.*h)).flatten() # to flat でgradに代入できるように
-
- all_us[idx] = tmp_val
- it.iternext()
- grad_idx += 1
-
- return np.array(grad)
-
-class NMPCControllerWithNewton():
- """
- Attributes
- ------------
- N : int
- predicte step, discritize value
- threshold : float
- newton's threshold value
- NUM_INPUT : int
- system input length, this should include dummy u and constraint variables
- MAX_ITERATION : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.N = 10 # time step
- self.threshold = 0.0001 # break
-
- self.NUM_ALL_INPUT = 3 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.NUM_INPUT = 1 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.Jacobian_size = self.NUM_ALL_INPUT * self.N
-
- # newton parameters
- self.MAX_ITERATION = 100
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros((self.N, self.NUM_INPUT))
- self.dummy_us = np.ones((self.N, self.NUM_INPUT)) * 0.25
- self.raws = np.ones((self.N, self.NUM_INPUT)) * 0.01
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = 0.01
-
- # concat all us, shape (pred_len, input_size)
- all_us = np.hstack((self.us, self.dummy_us, self.raws))
-
- # Newton method
- for i in range(self.MAX_ITERATION):
- # calc all state
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- # F
- F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # judge
- if np.linalg.norm(F_hat) < self.threshold:
- # print("break!!")
- break
-
- grad_f = lambda x_1s, x_2s, lam_1s, lam_2s, all_us : self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
- forward_prop_f = lambda us : self.simulator.calc_predict_and_adjoint_state(x_1, x_2, us, self.N, dt)
- grads = calc_numerical_gradient(forward_prop_f, grad_f, all_us, (self.Jacobian_size, self.Jacobian_size), self.NUM_INPUT)
-
- # make jacobian and calc inverse of it
- # grads += np.eye(self.Jacobian_size) * 1e-8
- try:
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
- except np.linalg.LinAlgError:
- print("Warning : singular matrix!!")
- grads += np.eye(self.Jacobian_size) * 1e-10 # add noise
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
-
- all_us = all_us.reshape(self.N, self.NUM_ALL_INPUT)
-
- # update
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- # final insert
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, all_us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = np.zeros((N, self.NUM_INPUT*3))
-
- us = all_us[:, :self.NUM_INPUT].flatten()
- dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT].flatten()
- raws = all_us[:, 2*self.NUM_INPUT:].flatten()
-
- for i in range(N):
- F_u = 0.5 * us[i] + lam_2s[i] + 2. * raws[i] * us[i]
- F_dummy = -0.01 + 2. * raws[i] * dummy_us[i]
- F_raw = us[i]**2 + dummy_us[i]**2 - 0.5**2
-
- F[i] = np.array([F_u, F_dummy, F_raw])
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCControllerWithNewton()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- print("iteration = {}".format(i))
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/scripts/simple_run.py b/scripts/simple_run.py
new file mode 100644
index 0000000..510e24e
--- /dev/null
+++ b/scripts/simple_run.py
@@ -0,0 +1,53 @@
+import argparse
+
+from PythonLinearNonlinearControl.helper import bool_flag, make_logger
+from PythonLinearNonlinearControl.controllers.make_controllers import make_controller
+from PythonLinearNonlinearControl.planners.make_planners import make_planner
+from PythonLinearNonlinearControl.configs.make_configs import make_config
+from PythonLinearNonlinearControl.models.make_models import make_model
+from PythonLinearNonlinearControl.envs.make_envs import make_env
+from PythonLinearNonlinearControl.runners.make_runners import make_runner
+from PythonLinearNonlinearControl.plotters.plot_func import plot_results
+
+def run(args):
+ # logger
+ make_logger(args.result_dir)
+
+ # make envs
+ env = make_env(args)
+
+ # make config
+ config = make_config(args)
+
+ # make planner
+ planner = make_planner(args, config)
+
+ # make model
+ model = make_model(args, config)
+
+ # make controller
+ controller = make_controller(args, config, model)
+
+ # make simulator
+ runner = make_runner(args)
+
+ # run experiment
+ history_x, history_u, history_g = runner.run(env, controller, planner)
+
+ # plot results
+ plot_results(args, history_x, history_u, history_g=history_g)
+
+def main():
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--controller_type", type=str, default="MPC")
+ parser.add_argument("--planner_type", type=str, default="const")
+ parser.add_argument("--env", type=str, default="FirstOrderLag")
+ parser.add_argument("--result_dir", type=str, default="./result")
+
+ args = parser.parse_args()
+
+ run(args)
+
+if __name__ == "__main__":
+ main()
\ No newline at end of file
diff --git a/setup.py b/setup.py
new file mode 100644
index 0000000..7ea6a7c
--- /dev/null
+++ b/setup.py
@@ -0,0 +1,21 @@
+from setuptools import find_packages
+from setuptools import setup
+
+install_requires = ['numpy', 'matplotlib', 'cvxopt']
+tests_require = ['pytest']
+setup_requires = ["pytest-runner"]
+
+setup(
+ name='PythonLinearNonlinearControl',
+ version='2.0',
+ description='Implementing linear and non-linear control method in python',
+ author='Shunichi Sekiguchi',
+ author_email='quick1st97of@gmail.com',
+ install_requires=install_requires,
+ url='https://github.com/Shunichi09/PythonLinearNonlinearControl',
+ license='MIT License',
+ packages=find_packages(exclude=('tests')),
+ setup_requires=setup_requires,
+ test_suite='tests',
+ tests_require=tests_require
+)
\ No newline at end of file
diff --git a/tests/__init__.py b/tests/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/__init__.py b/tests/configs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/test_first_order_lag.py b/tests/configs/test_first_order_lag.py
new file mode 100644
index 0000000..a013fac
--- /dev/null
+++ b/tests/configs/test_first_order_lag.py
@@ -0,0 +1,34 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.configs.first_order_lag \
+ import FirstOrderLagConfigModule
+
+class TestCalcCost():
+ def test_calc_costs(self):
+ # make config
+ config = FirstOrderLagConfigModule()
+ # set
+ pred_len = 5
+ state_size = 4
+ input_size = 2
+ pop_size = 2
+ pred_xs = np.ones((pop_size, pred_len, state_size))
+ g_xs = np.ones((pop_size, pred_len, state_size)) * 0.5
+ input_samples = np.ones((pop_size, pred_len, input_size)) * 0.5
+
+ costs = config.input_cost_fn(input_samples)
+ expected_costs = np.ones((pop_size, pred_len, input_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.R))
+
+ costs = config.state_cost_fn(pred_xs, g_xs)
+ expected_costs = np.ones((pop_size, pred_len, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Q))
+
+ costs = config.terminal_state_cost_fn(pred_xs[:, -1, :],\
+ g_xs[:, -1, :])
+ expected_costs = np.ones((pop_size, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Sf))
\ No newline at end of file
diff --git a/tests/models/__init__.py b/tests/models/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/models/test_model.py b/tests/models/test_model.py
new file mode 100644
index 0000000..e11a439
--- /dev/null
+++ b/tests/models/test_model.py
@@ -0,0 +1,53 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.models.model import LinearModel
+
+class TestLinearModel():
+ """
+ """
+ def test_predict(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ assert pred_xs == pytest.approx(np.array([[0.5, 0.5], [0.75, 1.3]]))
+
+ def test_alltogether(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ u = np.tile(u, (1, 1, 1))
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)[0]
+
+ assert pred_xs_alltogether == pytest.approx(pred_xs)
+
+ def test_alltogether_val(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.stack((np.ones((1, 1)), np.ones((1, 1))*0.5), axis=0)
+
+ linear_model = LinearModel(A, B)
+
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)
+
+ expected_val = np.array([[[0.5, 0.5], [0.75, 1.3]],
+ [[0.5, 0.5], [0.65, 1.05]]])
+
+ assert pred_xs_alltogether == pytest.approx(expected_val)
\ No newline at end of file
 -
-
-
- -
-
-- track the goal
-
-
-
-
-
-- track the goal
-
-
- -
-
-
- -
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-
-- study wolf
-https://github.com/studywolf/control
-
-- Sergey Levine's lecture
-http://rail.eecs.berkeley.edu/deeprlcourse/
-
-- Tassa, Y., Erez, T., & Todorov, E. (2012). Synthesis and stabilization of complex behaviors through online trajectory optimization. IEEE International Conference on Intelligent Robots and Systems, 4906–4913. https://doi.org/10.1109/IROS.2012.6386025
-
-- Li, W., & Todorov, E. (n.d.). Iterative Linear Quadratic Regulator Design for Nonlinear Biological Movement Systems. Retrieved from https://homes.cs.washington.edu/~todorov/papers/LiICINCO04.pdf
diff --git a/ilqr/animation.py b/ilqr/animation.py
deleted file mode 100644
index ccb3b0d..0000000
--- a/ilqr/animation.py
+++ /dev/null
@@ -1,297 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.car_history_state = objects[0]
- self.target = objects[1]
-
- self.history_target_x = [self.target[:, 0]]
- self.history_target_y = [self.target[:, 1]]
-
- self.history_xs = [self.car_history_state[:, 0]]
- self.history_ys = [self.car_history_state[:, 1]]
- self.history_ths = [self.car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure()
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=10):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 2
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 2
- HIGH_MARGIN = 2
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], "*", color="b")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 1.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # goal
- self.traj_imgs[-1].set_data(self.history_target_x[0][i-1], self.history_target_y[0][i-1])
-
- # traj_ref
- self.traj_imgs[1].set_data(self.history_target_x[0][:i], self.history_target_y[0][:i])
\ No newline at end of file
diff --git a/ilqr/goal_maker.py b/ilqr/goal_maker.py
deleted file mode 100644
index 2112006..0000000
--- a/ilqr/goal_maker.py
+++ /dev/null
@@ -1,117 +0,0 @@
-import numpy as np
-import math
-import matplotlib.pyplot as plt
-
-def make_trajectory(goal_type, N):
- """
- Parameters
- -------------
- goal_type : str
- goal type
- N : int
- length of reference trajectory
- Returns
- -----------
- ref_trajectory : numpy.ndarray, shape(N, STATE_SIZE)
-
- Notes
- ---------
- this function can only deal with the
- """
-
- if goal_type == "const":
- ref_trajectory = np.array([[5., 3., 0.]])
-
- return ref_trajectory
-
- if goal_type == "sin":
- # parameters
- amplitude = 2.
- num_period = 2.
-
- ref_x_trajectory = np.linspace(0., 2 * math.pi * num_period, N)
- ref_y_trajectory = amplitude * np.sin(ref_x_trajectory)
-
- ref_xy_trajectory = np.stack((ref_x_trajectory, ref_y_trajectory))
-
- # target of theta is always zero
- ref_trajectory = np.vstack((ref_xy_trajectory, np.zeros((1, N))))
-
- return ref_trajectory.T
-
-class GoalMaker():
- """
- Attributes
- -----------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- ref_traj : numpy.ndarray, shape(N, STATE_SIZE)
- in this case the state size is 3
- """
-
- def __init__(self, N=500, goal_type="const", dt=0.01):
- """
- Parameters
- --------------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- """
- self.N = N
- self.goal_type = goal_type
- self.dt = dt
-
- self.ref_traj = None
- self.history_target = []
-
- def preprocess(self):
- """preprocess of make goal
- """
- goal_type_list = ["const", "sin"]
-
- if self.goal_type not in goal_type_list:
- raise KeyError("{0} is not in implemented goal type. please implement that!!".format(self.goal_type))
-
- self.ref_traj = make_trajectory(self.goal_type, self.N)
-
- def calc_goal(self, x):
- """ calclate nearest goal
- Parameters
- ------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- state of the system
-
- Returns
- ------------
- goal : numpy.ndarray, shape(STATE_SIZE, )
- """
-
- # search nearest point
- x_dis = (self.ref_traj[:, 0]-x[0])**2
- y_dis = (self.ref_traj[:, 1]-x[1])**2
- index = np.argmin(np.sqrt(x_dis + y_dis))
-
- print(index)
-
- MARGIN = 30
- if not self.goal_type == "const":
- index += MARGIN
-
- if index > self.N-1:
- index = self.N - 1
-
- goal = self.ref_traj[index]
-
- self.history_target.append(goal)
-
- return goal
-
-if __name__ == "__main__":
- make_trajectory("sin", 400)
\ No newline at end of file
diff --git a/ilqr/ilqr.py b/ilqr/ilqr.py
deleted file mode 100644
index 21a0c16..0000000
--- a/ilqr/ilqr.py
+++ /dev/null
@@ -1,463 +0,0 @@
-import numpy as np
-from copy import copy, deepcopy
-
-from model import TwoWheeledCar
-
-class iLQRController():
- """
- A controller that implements iterative Linear Quadratic control.
- Controls the (x, y, th) of the two wheeled car
-
- Attributes:
- ------------
- tN : int
- number of time step
- STATE_SIZE : int
- system state size
- INPUT_SIZE : int
- system input size
- dt : float
- sampling time
- max_iter : int
- number of max iteration
- lamb_factor : int
- lambda factor is that the adding value to make the matrix of Q _uu be positive
- lamb_max : float
- maximum lambda value to make the matrix of Q _uu be positive
- eps_converge : float
- threshold value of the iteration
- """
-
- def __init__(self, N=100, max_iter=400, dt=0.01):
- """
- Parameters
- ----------
- N : int, optional
- number of time step, default is 100
- max_iter : int, optional
- number of max iteration, default is 400
- dt : float, optional
- sampling time, default is 0.01
- """
- self.tN = N
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
- self.dt = dt
-
- self.max_iter = max_iter
- self.lamb_factor = 10
- self.lamb_max = 1e4
- self.eps_converge = 0.001
-
- def calc_input(self, car, x_target):
- """main loop of iterative LQR
-
- Parameters
- -------------
- car : model class
- should have initialize state and update state
- x_target : numpy.ndarray, shape(STATE_SIZE, )
- target state
-
- Returns
- -----------
- u : numpy.ndarray, shape(INPUT_SIZE, )
-
- See also
- ----------
- model.py
- """
-
- # initialize
- self.reset(x_target)
-
- # Compute the optimization
- x0 = np.zeros(self.STATE_SIZE)
- self.simulator, x0 = self.initialize_simulator(car)
- U = np.copy(self.U)
- self.X, self.U, cost = self.ilqr(x0, U)
-
- self.u = self.U[self.t] # use only one time step (like MPC)
-
- return self.u
-
- def initialize_simulator(self, car):
- """ make copy for controller
- Parameters
- -------------
- car : model class
- should have initialize state and update state
-
- Returns
- ----------
- simulator : model class
- should have initialize state and update state
- x0 : numpy.ndarray, shape(STATE_SIZE)
- initial state of the simulator
- """
- # copy
- simulator = TwoWheeledCar(deepcopy(car.xs))
-
- return simulator, deepcopy(simulator.xs)
-
- def cost(self, xs, us):
- """ the immediate state cost function
-
- Parameters
- ------------
- xs : shape(STATE_SIZE, tN + 1)
- predict state of the system
- us : shape(STATE_SIZE, tN)
- predict input of the system
-
- Returns
- ----------
- l : float
- stage cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- l_u : numpy.ndarray, shape(INPUT_SIZE, )
- differential of stage cost by u
- l_uu : numpy.ndarray, shape(INPUT_SIZE, INPUT_SIZE)
- second order differential of stage cost by uu
- l_ux numpy.ndarray, shape(INPUT_SIZE, STATE_SIZE)
- second order differential of stage cost by ux
- """
-
- # total cost
- R_11 = 1e-4 # terminal u_v cost weight
- R_22 = 1e-4 # terminal u_th cost weight
-
- l = np.dot(us.T, np.dot(np.diag([R_11, R_22]), us))
-
- # compute derivatives of cost
- l_x = np.zeros(self.STATE_SIZE)
- l_xx = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- l_u1 = 2. * us[0] * R_11
- l_u2 = 2. * us[1] * R_22
-
- l_u = np.array([l_u1, l_u2])
-
- l_uu = 2. * np.diag([R_11, R_22])
-
- l_ux = np.zeros((self.INPUT_SIZE, self.STATE_SIZE))
-
- return l, l_x, l_xx, l_u, l_uu, l_ux
-
- def cost_final(self, x):
- """ the final state cost function
-
- Parameters
- -------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- predict state of the system
-
- Returns
- ---------
- l : float
- terminal cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- """
- Q_11 = 10. # terminal x cost weight
- Q_22 = 10. # terminal y cost weight
- Q_33 = 0.1 # terminal theta cost weight
-
- error = self.simulator.xs - self.target
-
- l = np.dot(error.T, np.dot(np.diag([Q_11, Q_22, Q_33]), error))
-
- # about L_x
- l_x1 = 2. * (x[0] - self.target[0]) * Q_11
- l_x2 = 2. * (x[1] - self.target[1]) * Q_22
- l_x3 = 2. * (x[2] -self.target[2]) * Q_33
- l_x = np.array([l_x1, l_x2, l_x3])
-
- # about l_xx
- l_xx = 2. * np.diag([Q_11, Q_22, Q_33])
-
- # Final cost only requires these three values
- return l, l_x, l_xx
-
- def finite_differences(self, x, u):
- """ calculate gradient of plant dynamics using finite differences
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE,)
- the control input
-
- Returns
- ------------
- A : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- differential of the model /alpha X
- B : numpy.ndarray, shape(STATE_SIZE, INPUT_SIZE)
- differential of the model /alpha U
-
- Notes
- -------
- in this case, I pre-calculated the differential of the model because the tow-wheeled model is not difficult to calculate the gradient.
- If you dont or cannot do that, you can use the numerical differentiation.
- However, sometimes the the numerical differentiation affect the accuracy of calculations.
- """
-
- A = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
- A_ideal = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- B = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
- B_ideal = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- eps = 1e-4 # finite differences epsilon
-
- for ii in range(self.STATE_SIZE):
- # calculate partial differential w.r.t. x
- inc_x = x.copy()
- inc_x[ii] += eps
- state_inc,_ = self.plant_dynamics(inc_x, u.copy())
- dec_x = x.copy()
- dec_x[ii] -= eps
- state_dec,_ = self.plant_dynamics(dec_x, u.copy())
- A[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- A_ideal[0, 2] = -np.sin(x[2]) * u[0]
- A_ideal[1, 2] = np.cos(x[2]) * u[0]
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- for ii in range(self.INPUT_SIZE):
- # calculate partial differential w.r.t. u
- inc_u = u.copy()
- inc_u[ii] += eps
- state_inc,_ = self.plant_dynamics(x.copy(), inc_u)
- dec_u = u.copy()
- dec_u[ii] -= eps
- state_dec,_ = self.plant_dynamics(x.copy(), dec_u)
- B[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- B_ideal[0, 0] = np.cos(x[2])
- B_ideal[1, 0] = np.sin(x[2])
- B_ideal[2, 1] = 1.
-
- return A_ideal, B_ideal
-
- def ilqr(self, x0, U=None):
- """ use iterative linear quadratic regulation to find a control
- sequence that minimizes the cost function
-
- Parameters
- --------------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray(TIME, INPUT_SIZE)
- the initial control trajectory dimension
- """
- U = self.U if U is None else U
-
- lamb = 1.0 # regularization parameter
- sim_new_trajectory = True
- tN = U.shape[0] # number of time steps
-
- for ii in range(self.max_iter):
-
- if sim_new_trajectory == True:
- # simulate forward using the current control trajectory
- X, cost = self.simulate(x0, U)
- oldcost = np.copy(cost) # copy for exit condition check
-
- #
- f_x = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # df / dx
- f_u = np.zeros((tN, self.STATE_SIZE, self.INPUT_SIZE)) # df / du
- # for storing quadratized cost function
-
- l = np.zeros((tN,1)) # immediate state cost
- l_x = np.zeros((tN, self.STATE_SIZE)) # dl / dx
- l_xx = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # d^2 l / dx^2
- l_u = np.zeros((tN, self.INPUT_SIZE)) # dl / du
- l_uu = np.zeros((tN, self.INPUT_SIZE, self.INPUT_SIZE)) # d^2 l / du^2
- l_ux = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # d^2 l / du / dx
- # for everything except final state
- for t in range(tN-1):
- # x(t+1) = f(x(t), u(t)) = x(t) + dx(t) * dt
- # linearized dx(t) = np.dot(A(t), x(t)) + np.dot(B(t), u(t))
- # f_x = (np.eye + A(t)) * dt
- # f_u = (B(t)) * dt
- # continuous --> discrete
- A, B = self.finite_differences(X[t], U[t])
- f_x[t] = np.eye(self.STATE_SIZE) + A * self.dt
- f_u[t] = B * self.dt
-
- """ NOTE: why multiply dt in original program ??
- So the dt multiplication and + I is because we’re actually taking the derivative of the state with respect to the previous state. Which is not
- dx = Ax + Bu,
- but rather
- x(t) = x(t-1) + (Ax(t-1) + Bu(t-1))*dt
- And that’s where the identity matrix and dt come from!
- So that part’s in the comments of the code, but the *dt on all the cost function stuff is not commented on at all!
- So here the dt lets you normalize behaviour for different time steps (assuming you also scale the number of steps in the sequence).
- So if you have a time step of .01 or .001 you’re not racking up 10 times as much cost function in the latter case.
- And if you run the code with 50 steps in the sequence and dt=.01 and 500 steps in the sequence
- and dt=.001 you’ll see that you get the same results, which is not the case at all when you don’t take dt into account in the cost function!
- """
-
- (l[t], l_x[t], l_xx[t], l_u[t], l_uu[t], l_ux[t]) = self.cost(X[t], U[t])
-
- l[t] *= self.dt
- l_x[t] *= self.dt
- l_xx[t] *= self.dt
- l_u[t] *= self.dt
- l_uu[t] *= self.dt
- l_ux[t] *= self.dt
-
- # and for final state
- l[-1], l_x[-1], l_xx[-1] = self.cost_final(X[-1])
-
- sim_new_trajectory = False
-
- V = l[-1].copy() # value function
- V_x = l_x[-1].copy() # dV / dx
- V_xx = l_xx[-1].copy() # d^2 V / dx^2
- k = np.zeros((tN, self.INPUT_SIZE)) # feedforward modification
- K = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # feedback gain
-
- # work backwards to solve for V, Q, k, and K
- for t in range(self.tN-2, -1, -1):
- Q_x = l_x[t] + np.dot(f_x[t].T, V_x)
- Q_u = l_u[t] + np.dot(f_u[t].T, V_x)
-
- Q_xx = l_xx[t] + np.dot(f_x[t].T, np.dot(V_xx, f_x[t]))
- Q_ux = l_ux[t] + np.dot(f_u[t].T, np.dot(V_xx, f_x[t]))
- Q_uu = l_uu[t] + np.dot(f_u[t].T, np.dot(V_xx, f_u[t]))
-
- Q_uu_evals, Q_uu_evecs = np.linalg.eig(Q_uu)
- Q_uu_evals[Q_uu_evals < 0] = 0.0
- Q_uu_evals += lamb
- Q_uu_inv = np.dot(Q_uu_evecs, np.dot(np.diag(1.0/Q_uu_evals), Q_uu_evecs.T))
-
- k[t] = -1. * np.dot(Q_uu_inv, Q_u)
- K[t] = -1. * np.dot(Q_uu_inv, Q_ux)
-
- V_x = Q_x - np.dot(K[t].T, np.dot(Q_uu, k[t]))
- V_xx = Q_xx - np.dot(K[t].T, np.dot(Q_uu, K[t]))
-
- U_new = np.zeros((tN, self.INPUT_SIZE))
- x_new = x0.copy()
- for t in range(tN - 1):
- # use feedforward (k) and feedback (K) gain matrices
- # calculated from our value function approximation
- U_new[t] = U[t] + k[t] + np.dot(K[t], x_new - X[t])
- _,x_new = self.plant_dynamics(x_new, U_new[t])
-
- # evaluate the new trajectory
- X_new, cost_new = self.simulate(x0, U_new)
-
- if cost_new < cost:
- # decrease lambda (get closer to Newton's method)
- lamb /= self.lamb_factor
-
- X = np.copy(X_new) # update trajectory
- U = np.copy(U_new) # update control signal
- oldcost = np.copy(cost)
- cost = np.copy(cost_new)
-
- sim_new_trajectory = True # do another rollout
-
- # check to see if update is small enough to exit
- if ii > 0 and ((abs(oldcost-cost)/cost) < self.eps_converge):
- print("Converged at iteration = %d; Cost = %.4f;"%(ii,cost_new) +
- " logLambda = %.1f"%np.log(lamb))
- break
-
- else:
- # increase lambda (get closer to gradient descent)
- lamb *= self.lamb_factor
- # print("cost: %.4f, increasing lambda to %.4f")%(cost, lamb)
- if lamb > self.lamb_max:
- print("lambda > max_lambda at iteration = %d;"%ii +
- " Cost = %.4f; logLambda = %.1f"%(cost,
- np.log(lamb)))
- break
-
- return X, U, cost
-
- def plant_dynamics(self, x, u):
- """ simulate a single time step of the plant, from
- initial state x and applying control signal u
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE, )
- the control signal
-
- Returns
- -----------
- xdot : numpy.ndarray, shape(STATE_SIZE, )
- the gradient of x
- x_next : numpy.ndarray, shape(STATE_SIZE, )
- next state of x
- """
- self.simulator.initialize_state(x)
-
- # apply the control signal
- x_next = self.simulator.update_state(u, self.dt)
-
- # calculate the change in state
- xdot = ((x_next - x) / self.dt).squeeze()
-
- return xdot, x_next
-
- def reset(self, target):
- """ reset the state of the system """
-
- # Index along current control sequence
- self.t = 0
- self.U = np.zeros((self.tN, self.INPUT_SIZE))
- self.target = target.copy()
-
- def simulate(self, x0, U):
- """ do a rollout of the system, starting at x0 and
- applying the control sequence U
-
- Parameters
- ----------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray, shape(tN, INPUT_SIZE)
- the control sequence to apply
-
- Returns
- ---------
- X : numpy.ndarray, shape(tN, STATE_SIZE)
- the state sequence
- cost : float
- cost
- """
-
- tN = U.shape[0]
- X = np.zeros((tN, self.STATE_SIZE))
- X[0] = x0
- cost = 0
-
- # Run simulation with substeps
- for t in range(tN-1):
- _,X[t+1] = self.plant_dynamics(X[t], U[t])
- l, _ , _, _ , _ , _ = self.cost(X[t], U[t])
- cost = cost + self.dt * l
-
- # Adjust for final cost, subsample trajectory
- l_f, _, _ = self.cost_final(X[-1])
- cost = cost + l_f
-
- return X, cost
diff --git a/ilqr/main_dynamic.py b/ilqr/main_dynamic.py
deleted file mode 100644
index c6b22d6..0000000
--- a/ilqr/main_dynamic.py
+++ /dev/null
@@ -1,66 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="sin")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/main_static.py b/ilqr/main_static.py
deleted file mode 100644
index 3cceb82..0000000
--- a/ilqr/main_static.py
+++ /dev/null
@@ -1,68 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="const")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
-
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/model.py b/ilqr/model.py
deleted file mode 100644
index 4030c8f..0000000
--- a/ilqr/model.py
+++ /dev/null
@@ -1,131 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-
-"""
-このWheeled modelはコントローラー用
-ホントはbase作って、継承すべきですが省略
-"""
-class TwoWheeledCar():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
-
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt):
- """
- Palameters
- ------------
- us : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
- return self.xs.copy()
-
- def initialize_state(self, init_xs):
- """
- initialize the state
-
- Parameters
- ------------
- init_xs : numpy.ndarray
- """
- self.xs = init_xs.flatten()
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
\ No newline at end of file
diff --git a/mpc/basic/README.md b/mpc/basic/README.md
deleted file mode 100644
index 0d64664..0000000
--- a/mpc/basic/README.md
+++ /dev/null
@@ -1,146 +0,0 @@
-# Model Predictive Control Basic Tool
-This program is about template, generic function of linear model predictive control
-
-# Documentation of the MPC function
-Linear model predicitive control should have state equation.
-So if you want to use this function, you should model the plant as state equation.
-Therefore, the parameters of this class are as following
-
-**class MpcController()**
-
-Attributes :
-
-- A : numpy.ndarray
- - system matrix
-- B : numpy.ndarray
- - input matrix
-- Q : numpy.ndarray
- - evaluation function weight for states
-- Qs : numpy.ndarray
- - concatenated evaluation function weight for states
-- R : numpy.ndarray
- - evaluation function weight for inputs
-- Rs : numpy.ndarray
- - concatenated evaluation function weight for inputs
-- pre_step : int
- - prediction step
-- state_size : int
- - state size of the plant
-- input_size : int
- - input size of the plant
-- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-- input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-
-Methods:
-
-- initialize_controller() initialize the controller
-- calc_input(states, references) calculating optimal input
-
-More details, please look the **mpc_func_with_scipy.py** and **mpc_func_with_cvxopt.py**
-
-We have two function, mpc_func_with_cvxopt.py and mpc_func_with_scipy.py
-Both functions have same variable and member function. However the solver is different.
-Plese choose the right method for your environment.
-
-- example of import
-
-```py
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-```
-
-# Examples
-## Problem Formulation
-
-- **first order system**
-
-
-
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-
-- study wolf
-https://github.com/studywolf/control
-
-- Sergey Levine's lecture
-http://rail.eecs.berkeley.edu/deeprlcourse/
-
-- Tassa, Y., Erez, T., & Todorov, E. (2012). Synthesis and stabilization of complex behaviors through online trajectory optimization. IEEE International Conference on Intelligent Robots and Systems, 4906–4913. https://doi.org/10.1109/IROS.2012.6386025
-
-- Li, W., & Todorov, E. (n.d.). Iterative Linear Quadratic Regulator Design for Nonlinear Biological Movement Systems. Retrieved from https://homes.cs.washington.edu/~todorov/papers/LiICINCO04.pdf
diff --git a/ilqr/animation.py b/ilqr/animation.py
deleted file mode 100644
index ccb3b0d..0000000
--- a/ilqr/animation.py
+++ /dev/null
@@ -1,297 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.car_history_state = objects[0]
- self.target = objects[1]
-
- self.history_target_x = [self.target[:, 0]]
- self.history_target_y = [self.target[:, 1]]
-
- self.history_xs = [self.car_history_state[:, 0]]
- self.history_ys = [self.car_history_state[:, 1]]
- self.history_ths = [self.car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure()
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=10):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 2
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 2
- HIGH_MARGIN = 2
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], "*", color="b")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 1.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # goal
- self.traj_imgs[-1].set_data(self.history_target_x[0][i-1], self.history_target_y[0][i-1])
-
- # traj_ref
- self.traj_imgs[1].set_data(self.history_target_x[0][:i], self.history_target_y[0][:i])
\ No newline at end of file
diff --git a/ilqr/goal_maker.py b/ilqr/goal_maker.py
deleted file mode 100644
index 2112006..0000000
--- a/ilqr/goal_maker.py
+++ /dev/null
@@ -1,117 +0,0 @@
-import numpy as np
-import math
-import matplotlib.pyplot as plt
-
-def make_trajectory(goal_type, N):
- """
- Parameters
- -------------
- goal_type : str
- goal type
- N : int
- length of reference trajectory
- Returns
- -----------
- ref_trajectory : numpy.ndarray, shape(N, STATE_SIZE)
-
- Notes
- ---------
- this function can only deal with the
- """
-
- if goal_type == "const":
- ref_trajectory = np.array([[5., 3., 0.]])
-
- return ref_trajectory
-
- if goal_type == "sin":
- # parameters
- amplitude = 2.
- num_period = 2.
-
- ref_x_trajectory = np.linspace(0., 2 * math.pi * num_period, N)
- ref_y_trajectory = amplitude * np.sin(ref_x_trajectory)
-
- ref_xy_trajectory = np.stack((ref_x_trajectory, ref_y_trajectory))
-
- # target of theta is always zero
- ref_trajectory = np.vstack((ref_xy_trajectory, np.zeros((1, N))))
-
- return ref_trajectory.T
-
-class GoalMaker():
- """
- Attributes
- -----------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- ref_traj : numpy.ndarray, shape(N, STATE_SIZE)
- in this case the state size is 3
- """
-
- def __init__(self, N=500, goal_type="const", dt=0.01):
- """
- Parameters
- --------------
- N : int
- length of reference
- goal_type : str
- goal type
- dt : float
- sampling time
- """
- self.N = N
- self.goal_type = goal_type
- self.dt = dt
-
- self.ref_traj = None
- self.history_target = []
-
- def preprocess(self):
- """preprocess of make goal
- """
- goal_type_list = ["const", "sin"]
-
- if self.goal_type not in goal_type_list:
- raise KeyError("{0} is not in implemented goal type. please implement that!!".format(self.goal_type))
-
- self.ref_traj = make_trajectory(self.goal_type, self.N)
-
- def calc_goal(self, x):
- """ calclate nearest goal
- Parameters
- ------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- state of the system
-
- Returns
- ------------
- goal : numpy.ndarray, shape(STATE_SIZE, )
- """
-
- # search nearest point
- x_dis = (self.ref_traj[:, 0]-x[0])**2
- y_dis = (self.ref_traj[:, 1]-x[1])**2
- index = np.argmin(np.sqrt(x_dis + y_dis))
-
- print(index)
-
- MARGIN = 30
- if not self.goal_type == "const":
- index += MARGIN
-
- if index > self.N-1:
- index = self.N - 1
-
- goal = self.ref_traj[index]
-
- self.history_target.append(goal)
-
- return goal
-
-if __name__ == "__main__":
- make_trajectory("sin", 400)
\ No newline at end of file
diff --git a/ilqr/ilqr.py b/ilqr/ilqr.py
deleted file mode 100644
index 21a0c16..0000000
--- a/ilqr/ilqr.py
+++ /dev/null
@@ -1,463 +0,0 @@
-import numpy as np
-from copy import copy, deepcopy
-
-from model import TwoWheeledCar
-
-class iLQRController():
- """
- A controller that implements iterative Linear Quadratic control.
- Controls the (x, y, th) of the two wheeled car
-
- Attributes:
- ------------
- tN : int
- number of time step
- STATE_SIZE : int
- system state size
- INPUT_SIZE : int
- system input size
- dt : float
- sampling time
- max_iter : int
- number of max iteration
- lamb_factor : int
- lambda factor is that the adding value to make the matrix of Q _uu be positive
- lamb_max : float
- maximum lambda value to make the matrix of Q _uu be positive
- eps_converge : float
- threshold value of the iteration
- """
-
- def __init__(self, N=100, max_iter=400, dt=0.01):
- """
- Parameters
- ----------
- N : int, optional
- number of time step, default is 100
- max_iter : int, optional
- number of max iteration, default is 400
- dt : float, optional
- sampling time, default is 0.01
- """
- self.tN = N
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
- self.dt = dt
-
- self.max_iter = max_iter
- self.lamb_factor = 10
- self.lamb_max = 1e4
- self.eps_converge = 0.001
-
- def calc_input(self, car, x_target):
- """main loop of iterative LQR
-
- Parameters
- -------------
- car : model class
- should have initialize state and update state
- x_target : numpy.ndarray, shape(STATE_SIZE, )
- target state
-
- Returns
- -----------
- u : numpy.ndarray, shape(INPUT_SIZE, )
-
- See also
- ----------
- model.py
- """
-
- # initialize
- self.reset(x_target)
-
- # Compute the optimization
- x0 = np.zeros(self.STATE_SIZE)
- self.simulator, x0 = self.initialize_simulator(car)
- U = np.copy(self.U)
- self.X, self.U, cost = self.ilqr(x0, U)
-
- self.u = self.U[self.t] # use only one time step (like MPC)
-
- return self.u
-
- def initialize_simulator(self, car):
- """ make copy for controller
- Parameters
- -------------
- car : model class
- should have initialize state and update state
-
- Returns
- ----------
- simulator : model class
- should have initialize state and update state
- x0 : numpy.ndarray, shape(STATE_SIZE)
- initial state of the simulator
- """
- # copy
- simulator = TwoWheeledCar(deepcopy(car.xs))
-
- return simulator, deepcopy(simulator.xs)
-
- def cost(self, xs, us):
- """ the immediate state cost function
-
- Parameters
- ------------
- xs : shape(STATE_SIZE, tN + 1)
- predict state of the system
- us : shape(STATE_SIZE, tN)
- predict input of the system
-
- Returns
- ----------
- l : float
- stage cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- l_u : numpy.ndarray, shape(INPUT_SIZE, )
- differential of stage cost by u
- l_uu : numpy.ndarray, shape(INPUT_SIZE, INPUT_SIZE)
- second order differential of stage cost by uu
- l_ux numpy.ndarray, shape(INPUT_SIZE, STATE_SIZE)
- second order differential of stage cost by ux
- """
-
- # total cost
- R_11 = 1e-4 # terminal u_v cost weight
- R_22 = 1e-4 # terminal u_th cost weight
-
- l = np.dot(us.T, np.dot(np.diag([R_11, R_22]), us))
-
- # compute derivatives of cost
- l_x = np.zeros(self.STATE_SIZE)
- l_xx = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- l_u1 = 2. * us[0] * R_11
- l_u2 = 2. * us[1] * R_22
-
- l_u = np.array([l_u1, l_u2])
-
- l_uu = 2. * np.diag([R_11, R_22])
-
- l_ux = np.zeros((self.INPUT_SIZE, self.STATE_SIZE))
-
- return l, l_x, l_xx, l_u, l_uu, l_ux
-
- def cost_final(self, x):
- """ the final state cost function
-
- Parameters
- -------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- predict state of the system
-
- Returns
- ---------
- l : float
- terminal cost
- l_x : numpy.ndarray, shape(STATE_SIZE, )
- differential of stage cost by x
- l_xx : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- second order differential of stage cost by x
- """
- Q_11 = 10. # terminal x cost weight
- Q_22 = 10. # terminal y cost weight
- Q_33 = 0.1 # terminal theta cost weight
-
- error = self.simulator.xs - self.target
-
- l = np.dot(error.T, np.dot(np.diag([Q_11, Q_22, Q_33]), error))
-
- # about L_x
- l_x1 = 2. * (x[0] - self.target[0]) * Q_11
- l_x2 = 2. * (x[1] - self.target[1]) * Q_22
- l_x3 = 2. * (x[2] -self.target[2]) * Q_33
- l_x = np.array([l_x1, l_x2, l_x3])
-
- # about l_xx
- l_xx = 2. * np.diag([Q_11, Q_22, Q_33])
-
- # Final cost only requires these three values
- return l, l_x, l_xx
-
- def finite_differences(self, x, u):
- """ calculate gradient of plant dynamics using finite differences
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE,)
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE,)
- the control input
-
- Returns
- ------------
- A : numpy.ndarray, shape(STATE_SIZE, STATE_SIZE)
- differential of the model /alpha X
- B : numpy.ndarray, shape(STATE_SIZE, INPUT_SIZE)
- differential of the model /alpha U
-
- Notes
- -------
- in this case, I pre-calculated the differential of the model because the tow-wheeled model is not difficult to calculate the gradient.
- If you dont or cannot do that, you can use the numerical differentiation.
- However, sometimes the the numerical differentiation affect the accuracy of calculations.
- """
-
- A = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
- A_ideal = np.zeros((self.STATE_SIZE, self.STATE_SIZE))
-
- B = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
- B_ideal = np.zeros((self.STATE_SIZE, self.INPUT_SIZE))
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- eps = 1e-4 # finite differences epsilon
-
- for ii in range(self.STATE_SIZE):
- # calculate partial differential w.r.t. x
- inc_x = x.copy()
- inc_x[ii] += eps
- state_inc,_ = self.plant_dynamics(inc_x, u.copy())
- dec_x = x.copy()
- dec_x[ii] -= eps
- state_dec,_ = self.plant_dynamics(dec_x, u.copy())
- A[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- A_ideal[0, 2] = -np.sin(x[2]) * u[0]
- A_ideal[1, 2] = np.cos(x[2]) * u[0]
-
- # if you want to use the numerical differentiation, please comment out this code
- """
- for ii in range(self.INPUT_SIZE):
- # calculate partial differential w.r.t. u
- inc_u = u.copy()
- inc_u[ii] += eps
- state_inc,_ = self.plant_dynamics(x.copy(), inc_u)
- dec_u = u.copy()
- dec_u[ii] -= eps
- state_dec,_ = self.plant_dynamics(x.copy(), dec_u)
- B[:, ii] = (state_inc - state_dec) / (2 * eps)
- """
-
- B_ideal[0, 0] = np.cos(x[2])
- B_ideal[1, 0] = np.sin(x[2])
- B_ideal[2, 1] = 1.
-
- return A_ideal, B_ideal
-
- def ilqr(self, x0, U=None):
- """ use iterative linear quadratic regulation to find a control
- sequence that minimizes the cost function
-
- Parameters
- --------------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray(TIME, INPUT_SIZE)
- the initial control trajectory dimension
- """
- U = self.U if U is None else U
-
- lamb = 1.0 # regularization parameter
- sim_new_trajectory = True
- tN = U.shape[0] # number of time steps
-
- for ii in range(self.max_iter):
-
- if sim_new_trajectory == True:
- # simulate forward using the current control trajectory
- X, cost = self.simulate(x0, U)
- oldcost = np.copy(cost) # copy for exit condition check
-
- #
- f_x = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # df / dx
- f_u = np.zeros((tN, self.STATE_SIZE, self.INPUT_SIZE)) # df / du
- # for storing quadratized cost function
-
- l = np.zeros((tN,1)) # immediate state cost
- l_x = np.zeros((tN, self.STATE_SIZE)) # dl / dx
- l_xx = np.zeros((tN, self.STATE_SIZE, self.STATE_SIZE)) # d^2 l / dx^2
- l_u = np.zeros((tN, self.INPUT_SIZE)) # dl / du
- l_uu = np.zeros((tN, self.INPUT_SIZE, self.INPUT_SIZE)) # d^2 l / du^2
- l_ux = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # d^2 l / du / dx
- # for everything except final state
- for t in range(tN-1):
- # x(t+1) = f(x(t), u(t)) = x(t) + dx(t) * dt
- # linearized dx(t) = np.dot(A(t), x(t)) + np.dot(B(t), u(t))
- # f_x = (np.eye + A(t)) * dt
- # f_u = (B(t)) * dt
- # continuous --> discrete
- A, B = self.finite_differences(X[t], U[t])
- f_x[t] = np.eye(self.STATE_SIZE) + A * self.dt
- f_u[t] = B * self.dt
-
- """ NOTE: why multiply dt in original program ??
- So the dt multiplication and + I is because we’re actually taking the derivative of the state with respect to the previous state. Which is not
- dx = Ax + Bu,
- but rather
- x(t) = x(t-1) + (Ax(t-1) + Bu(t-1))*dt
- And that’s where the identity matrix and dt come from!
- So that part’s in the comments of the code, but the *dt on all the cost function stuff is not commented on at all!
- So here the dt lets you normalize behaviour for different time steps (assuming you also scale the number of steps in the sequence).
- So if you have a time step of .01 or .001 you’re not racking up 10 times as much cost function in the latter case.
- And if you run the code with 50 steps in the sequence and dt=.01 and 500 steps in the sequence
- and dt=.001 you’ll see that you get the same results, which is not the case at all when you don’t take dt into account in the cost function!
- """
-
- (l[t], l_x[t], l_xx[t], l_u[t], l_uu[t], l_ux[t]) = self.cost(X[t], U[t])
-
- l[t] *= self.dt
- l_x[t] *= self.dt
- l_xx[t] *= self.dt
- l_u[t] *= self.dt
- l_uu[t] *= self.dt
- l_ux[t] *= self.dt
-
- # and for final state
- l[-1], l_x[-1], l_xx[-1] = self.cost_final(X[-1])
-
- sim_new_trajectory = False
-
- V = l[-1].copy() # value function
- V_x = l_x[-1].copy() # dV / dx
- V_xx = l_xx[-1].copy() # d^2 V / dx^2
- k = np.zeros((tN, self.INPUT_SIZE)) # feedforward modification
- K = np.zeros((tN, self.INPUT_SIZE, self.STATE_SIZE)) # feedback gain
-
- # work backwards to solve for V, Q, k, and K
- for t in range(self.tN-2, -1, -1):
- Q_x = l_x[t] + np.dot(f_x[t].T, V_x)
- Q_u = l_u[t] + np.dot(f_u[t].T, V_x)
-
- Q_xx = l_xx[t] + np.dot(f_x[t].T, np.dot(V_xx, f_x[t]))
- Q_ux = l_ux[t] + np.dot(f_u[t].T, np.dot(V_xx, f_x[t]))
- Q_uu = l_uu[t] + np.dot(f_u[t].T, np.dot(V_xx, f_u[t]))
-
- Q_uu_evals, Q_uu_evecs = np.linalg.eig(Q_uu)
- Q_uu_evals[Q_uu_evals < 0] = 0.0
- Q_uu_evals += lamb
- Q_uu_inv = np.dot(Q_uu_evecs, np.dot(np.diag(1.0/Q_uu_evals), Q_uu_evecs.T))
-
- k[t] = -1. * np.dot(Q_uu_inv, Q_u)
- K[t] = -1. * np.dot(Q_uu_inv, Q_ux)
-
- V_x = Q_x - np.dot(K[t].T, np.dot(Q_uu, k[t]))
- V_xx = Q_xx - np.dot(K[t].T, np.dot(Q_uu, K[t]))
-
- U_new = np.zeros((tN, self.INPUT_SIZE))
- x_new = x0.copy()
- for t in range(tN - 1):
- # use feedforward (k) and feedback (K) gain matrices
- # calculated from our value function approximation
- U_new[t] = U[t] + k[t] + np.dot(K[t], x_new - X[t])
- _,x_new = self.plant_dynamics(x_new, U_new[t])
-
- # evaluate the new trajectory
- X_new, cost_new = self.simulate(x0, U_new)
-
- if cost_new < cost:
- # decrease lambda (get closer to Newton's method)
- lamb /= self.lamb_factor
-
- X = np.copy(X_new) # update trajectory
- U = np.copy(U_new) # update control signal
- oldcost = np.copy(cost)
- cost = np.copy(cost_new)
-
- sim_new_trajectory = True # do another rollout
-
- # check to see if update is small enough to exit
- if ii > 0 and ((abs(oldcost-cost)/cost) < self.eps_converge):
- print("Converged at iteration = %d; Cost = %.4f;"%(ii,cost_new) +
- " logLambda = %.1f"%np.log(lamb))
- break
-
- else:
- # increase lambda (get closer to gradient descent)
- lamb *= self.lamb_factor
- # print("cost: %.4f, increasing lambda to %.4f")%(cost, lamb)
- if lamb > self.lamb_max:
- print("lambda > max_lambda at iteration = %d;"%ii +
- " Cost = %.4f; logLambda = %.1f"%(cost,
- np.log(lamb)))
- break
-
- return X, U, cost
-
- def plant_dynamics(self, x, u):
- """ simulate a single time step of the plant, from
- initial state x and applying control signal u
-
- Parameters
- --------------
- x : numpy.ndarray, shape(STATE_SIZE, )
- the state of the system
- u : numpy.ndarray, shape(INPUT_SIZE, )
- the control signal
-
- Returns
- -----------
- xdot : numpy.ndarray, shape(STATE_SIZE, )
- the gradient of x
- x_next : numpy.ndarray, shape(STATE_SIZE, )
- next state of x
- """
- self.simulator.initialize_state(x)
-
- # apply the control signal
- x_next = self.simulator.update_state(u, self.dt)
-
- # calculate the change in state
- xdot = ((x_next - x) / self.dt).squeeze()
-
- return xdot, x_next
-
- def reset(self, target):
- """ reset the state of the system """
-
- # Index along current control sequence
- self.t = 0
- self.U = np.zeros((self.tN, self.INPUT_SIZE))
- self.target = target.copy()
-
- def simulate(self, x0, U):
- """ do a rollout of the system, starting at x0 and
- applying the control sequence U
-
- Parameters
- ----------
- x0 : numpy.ndarray, shape(STATE_SIZE, )
- the initial state of the system
- U : numpy.ndarray, shape(tN, INPUT_SIZE)
- the control sequence to apply
-
- Returns
- ---------
- X : numpy.ndarray, shape(tN, STATE_SIZE)
- the state sequence
- cost : float
- cost
- """
-
- tN = U.shape[0]
- X = np.zeros((tN, self.STATE_SIZE))
- X[0] = x0
- cost = 0
-
- # Run simulation with substeps
- for t in range(tN-1):
- _,X[t+1] = self.plant_dynamics(X[t], U[t])
- l, _ , _, _ , _ , _ = self.cost(X[t], U[t])
- cost = cost + self.dt * l
-
- # Adjust for final cost, subsample trajectory
- l_f, _, _ = self.cost_final(X[-1])
- cost = cost + l_f
-
- return X, cost
diff --git a/ilqr/main_dynamic.py b/ilqr/main_dynamic.py
deleted file mode 100644
index c6b22d6..0000000
--- a/ilqr/main_dynamic.py
+++ /dev/null
@@ -1,66 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="sin")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/main_static.py b/ilqr/main_static.py
deleted file mode 100644
index 3cceb82..0000000
--- a/ilqr/main_static.py
+++ /dev/null
@@ -1,68 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-from model import TwoWheeledCar
-from ilqr import iLQRController
-from goal_maker import GoalMaker
-from animation import AnimDrawer
-
-
-def main():
- """
- """
- # iteration parameters
- NUM_ITERATIONS = 500
- dt = 0.01
-
- # make plant
- init_x = np.array([0., 0., 0.5*math.pi])
- car = TwoWheeledCar(init_x)
-
- # make goal
- goal_maker = GoalMaker(goal_type="const")
- goal_maker.preprocess()
-
- # controller
- controller = iLQRController()
-
- for iteration in range(NUM_ITERATIONS):
- print("iteration num = {} / {}".format(iteration, NUM_ITERATIONS))
-
- target = goal_maker.calc_goal(car.xs)
- u = controller.calc_input(car, target)
- car.update_state(u, dt) # update state
-
- # figures and animation
- history_states = np.array(car.history_xs)
- history_targets = np.array(goal_maker.history_target)
-
- time_fig = plt.figure()
-
- x_fig = time_fig.add_subplot(311)
- y_fig = time_fig.add_subplot(312)
- th_fig = time_fig.add_subplot(313)
-
- time = len(history_states)
-
- x_fig.plot(np.arange(time), history_states[:, 0], "r")
- x_fig.plot(np.arange(1, time), history_targets[:, 0], "b", linestyle="dashdot")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(time), history_states[:, 1], "r")
- y_fig.plot(np.arange(1, time), history_targets[:, 1], "b", linestyle="dashdot")
- y_fig.set_ylabel("y")
-
- th_fig.plot(np.arange(time), history_states[:, 2], "r")
- th_fig.plot(np.arange(1, time), history_targets[:, 2], "b", linestyle="dashdot")
- th_fig.set_ylabel("th")
-
- plt.show()
-
- history_states = np.array(car.history_xs)
-
- animdrawer = AnimDrawer([history_states, history_targets])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/ilqr/model.py b/ilqr/model.py
deleted file mode 100644
index 4030c8f..0000000
--- a/ilqr/model.py
+++ /dev/null
@@ -1,131 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-
-"""
-このWheeled modelはコントローラー用
-ホントはbase作って、継承すべきですが省略
-"""
-class TwoWheeledCar():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.STATE_SIZE = 3
- self.INPUT_SIZE = 2
-
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt):
- """
- Palameters
- ------------
- us : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
- return self.xs.copy()
-
- def initialize_state(self, init_xs):
- """
- initialize the state
-
- Parameters
- ------------
- init_xs : numpy.ndarray
- """
- self.xs = init_xs.flatten()
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
\ No newline at end of file
diff --git a/mpc/basic/README.md b/mpc/basic/README.md
deleted file mode 100644
index 0d64664..0000000
--- a/mpc/basic/README.md
+++ /dev/null
@@ -1,146 +0,0 @@
-# Model Predictive Control Basic Tool
-This program is about template, generic function of linear model predictive control
-
-# Documentation of the MPC function
-Linear model predicitive control should have state equation.
-So if you want to use this function, you should model the plant as state equation.
-Therefore, the parameters of this class are as following
-
-**class MpcController()**
-
-Attributes :
-
-- A : numpy.ndarray
- - system matrix
-- B : numpy.ndarray
- - input matrix
-- Q : numpy.ndarray
- - evaluation function weight for states
-- Qs : numpy.ndarray
- - concatenated evaluation function weight for states
-- R : numpy.ndarray
- - evaluation function weight for inputs
-- Rs : numpy.ndarray
- - concatenated evaluation function weight for inputs
-- pre_step : int
- - prediction step
-- state_size : int
- - state size of the plant
-- input_size : int
- - input size of the plant
-- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input dt, default is None
-- input_upper : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-- input_lower : numpy.ndarray, shape(input_size, ), optional
- - constraints of input, default is None
-
-Methods:
-
-- initialize_controller() initialize the controller
-- calc_input(states, references) calculating optimal input
-
-More details, please look the **mpc_func_with_scipy.py** and **mpc_func_with_cvxopt.py**
-
-We have two function, mpc_func_with_cvxopt.py and mpc_func_with_scipy.py
-Both functions have same variable and member function. However the solver is different.
-Plese choose the right method for your environment.
-
-- example of import
-
-```py
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-```
-
-# Examples
-## Problem Formulation
-
-- **first order system**
-
- -
-- input
-
-
-
-- input
-
- -
-- ACC (Adaptive cruise control)
-
-- time history of states
-
-
-
-- ACC (Adaptive cruise control)
-
-- time history of states
-
- -
-- animation
-
-
-
-- animation
-
- -
-
-# Usage
-
-- for example(first order system)
-
-```
-$ python main_example.py
-```
-
-- for example(ACC (Adaptive cruise control))
-
-```
-$ python main_ACC.py
-```
-
-- for comparing two methods of optimization solvers
-
-```
-$ python test_compare_methods.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-- cvxopt
-- scipy1.2.0 or more
-- python-control
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- モデル予測制御―制約のもとでの最適制御 著:Jan M. Maciejowski 訳:足立修一 東京電機大学出版局
\ No newline at end of file
diff --git a/mpc/basic/animation.py b/mpc/basic/animation.py
deleted file mode 100755
index 6ece541..0000000
--- a/mpc/basic/animation.py
+++ /dev/null
@@ -1,233 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
- """
- self.lead_car_history_state = objects[0]
- self.follow_car_history_state = objects[1]
-
- self.history_xs = [self.lead_car_history_state[:, 0], self.follow_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1], self.follow_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2], self.follow_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.object_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- # (2) set the xlim and ylim
- self.axis.set_xlim(-5, 50)
- self.axis.set_ylim(-2, 5)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.object_imgs.append(temp_img)
-
- traj_color_list = ["k", "m"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- self._draw_objects(i)
- self._draw_traj(i)
-
- return self.object_imgs, self.traj_imgs,
-
- def _draw_objects(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- for j in range(2):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[j][i],
- self.history_ys[j][i],
- 1.0,
- self.history_ths[j][i])
-
- self.object_imgs[fix_j].set_data([object_x, object_y])
- self.object_imgs[fix_j + 1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- for j in range(2):
- self.traj_imgs[j].set_data(self.history_xs[j][:i], self.history_ys[j][:i])
\ No newline at end of file
diff --git a/mpc/basic/main_ACC.py b/mpc/basic/main_ACC.py
deleted file mode 100644
index a868559..0000000
--- a/mpc/basic/main_ACC.py
+++ /dev/null
@@ -1,246 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- A = np.array([[0., V], [0., 0.]])
- B = np.array([[0.], [1.]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_ACC_TEMP.py b/mpc/basic/main_ACC_TEMP.py
deleted file mode 100644
index 9ad7c97..0000000
--- a/mpc/basic/main_ACC_TEMP.py
+++ /dev/null
@@ -1,243 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-# from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- Ad = np.array([[1., V * dt], [0., 1.]])
- Bd = np.array([[0.], [1. * dt]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- # sysc = matlab.ss(A, B, C, D)
- # discrete system
- # sysd = matlab.c2d(sysc, dt)
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_example.py b/mpc/basic/main_example.py
deleted file mode 100644
index b768a21..0000000
--- a/mpc/basic/main_example.py
+++ /dev/null
@@ -1,188 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_xs : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- D : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
- # print("xs = {0}".format(self.xs))
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
-def main():
- dt = 0.05
- simulation_time = 30 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- print(Ad)
- print(Bd)
- input()
-
- # evaluation function weight
- Q = np.diag([1., 1., 1., 1.])
- R = np.diag([1., 1.])
- pre_step = 10
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
- states = plant.xs
- opt_u = controller.calc_input(states, reference)
- plant.update_state(opt_u, dt=dt)
-
- history_states = np.array(plant.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 0])
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 1])
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 2])
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 3])
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us = np.array(controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 0])
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 1])
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_cvxopt.py b/mpc/basic/mpc_func_with_cvxopt.py
deleted file mode 100644
index 4e04736..0000000
--- a/mpc/basic/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,256 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_scipy.py b/mpc/basic/mpc_func_with_scipy.py
deleted file mode 100644
index 54ef3c9..0000000
--- a/mpc/basic/mpc_func_with_scipy.py
+++ /dev/null
@@ -1,262 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from scipy.optimize import minimize
-from scipy.optimize import LinearConstraint
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error) )
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- def optimized_func(dt_us):
- """
- """
- temp_dt_us = np.array([dt_us[i] for i in range(self.input_size * self.pre_step)])
-
- return (np.dot(temp_dt_us, np.dot(H, temp_dt_us.reshape(-1, 1))) - np.dot(G.T, temp_dt_us.reshape(-1, 1)))[0]
-
- # constraint
- lb = np.array([-np.inf for _ in range(len(ub))])
- linear_cons = LinearConstraint(A, lb, ub)
-
- init_dt_us = np.zeros(self.input_size * self.pre_step)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = minimize(optimized_func, init_dt_us, constraints=[linear_cons])
-
- opt_dt_us = opt_result.x
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/test_compare_methods.py b/mpc/basic/test_compare_methods.py
deleted file mode 100644
index 5ddaea4..0000000
--- a/mpc/basic/test_compare_methods.py
+++ /dev/null
@@ -1,211 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- states : float
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_state : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- C : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
-
- # print("xs = {0}".format(self.xs))
- # a = input()
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.history_xs)
-
-def main():
- dt = 0.05
- simulation_time = 50 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant_cvxopt = FirstOrderSystem(A, B, C, init_states=init_xs)
- plant_scipy = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1., 10., 10.])
- R = np.diag([0.01, 0.01])
- pre_step = 5
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller_cvxopt = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_scipy = MpcController_scipy(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_cvxopt.initialize_controller()
- controller_scipy.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
-
- states_cvxopt = plant_cvxopt.xs
- states_scipy = plant_scipy.xs
-
- opt_u_cvxopt = controller_cvxopt.calc_input(states_cvxopt, reference)
- opt_u_scipy = controller_scipy.calc_input(states_scipy, reference)
-
- plant_cvxopt.update_state(opt_u_cvxopt)
- plant_scipy.update_state(opt_u_scipy)
-
- history_states_cvxopt = np.array(plant_cvxopt.history_xs)
- history_states_scipy = np.array(plant_scipy.history_xs)
-
- time_history_fig = plt.figure(dpi=75)
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 0], label="cvxopt")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 0], label="scipy", linestyle="dashdot")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
- v_x_fig.legend()
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 1], label="cvxopt")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 1], label="scipy", linestyle="dashdot")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
- v_y_fig.legend()
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 2], label="cvxopt")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 2], label="scipy", linestyle="dashdot")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 3], label ="cvxopt")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 3], label="scipy", linestyle="dashdot")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us_cvxopt = np.array(controller_cvxopt.history_us)
- history_us_scipy = np.array(controller_scipy.history_us)
-
- input_history_fig = plt.figure(dpi=75)
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 0], label="cvxopt")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 0], label="scipy", linestyle="dashdot")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
- u_1_fig.legend()
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 1], label="cvxopt")
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 1], label="scipy", linestyle="dashdot")
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- u_2_fig.legend()
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/README.md b/mpc/extend/README.md
deleted file mode 100644
index e926aa5..0000000
--- a/mpc/extend/README.md
+++ /dev/null
@@ -1,41 +0,0 @@
-# Model Predictive Control for Vehicle model
-This program is for controlling the vehicle model.
-I implemented the steering control for vehicle by using Model Predictive Control.
-
-# Model
-Usually, the vehicle model is expressed by extremely complicated nonlinear equation.
-Acoording to reference 1, I used the simple model as shown in following equation.
-
-
-
-
-# Usage
-
-- for example(first order system)
-
-```
-$ python main_example.py
-```
-
-- for example(ACC (Adaptive cruise control))
-
-```
-$ python main_ACC.py
-```
-
-- for comparing two methods of optimization solvers
-
-```
-$ python test_compare_methods.py
-```
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-- cvxopt
-- scipy1.2.0 or more
-- python-control
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- モデル予測制御―制約のもとでの最適制御 著:Jan M. Maciejowski 訳:足立修一 東京電機大学出版局
\ No newline at end of file
diff --git a/mpc/basic/animation.py b/mpc/basic/animation.py
deleted file mode 100755
index 6ece541..0000000
--- a/mpc/basic/animation.py
+++ /dev/null
@@ -1,233 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
- """
- self.lead_car_history_state = objects[0]
- self.follow_car_history_state = objects[1]
-
- self.history_xs = [self.lead_car_history_state[:, 0], self.follow_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1], self.follow_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2], self.follow_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.object_imgs = []
- self.traj_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- # (2) set the xlim and ylim
- self.axis.set_xlim(-5, 50)
- self.axis.set_ylim(-2, 5)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.object_imgs.append(temp_img)
-
- traj_color_list = ["k", "m"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- self._draw_objects(i)
- self._draw_traj(i)
-
- return self.object_imgs, self.traj_imgs,
-
- def _draw_objects(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- for j in range(2):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[j][i],
- self.history_ys[j][i],
- 1.0,
- self.history_ths[j][i])
-
- self.object_imgs[fix_j].set_data([object_x, object_y])
- self.object_imgs[fix_j + 1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- for j in range(2):
- self.traj_imgs[j].set_data(self.history_xs[j][:i], self.history_ys[j][:i])
\ No newline at end of file
diff --git a/mpc/basic/main_ACC.py b/mpc/basic/main_ACC.py
deleted file mode 100644
index a868559..0000000
--- a/mpc/basic/main_ACC.py
+++ /dev/null
@@ -1,246 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- A = np.array([[0., V], [0., 0.]])
- B = np.array([[0.], [1.]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_ACC_TEMP.py b/mpc/basic/main_ACC_TEMP.py
deleted file mode 100644
index 9ad7c97..0000000
--- a/mpc/basic/main_ACC_TEMP.py
+++ /dev/null
@@ -1,243 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from animation import AnimDrawer
-# from control import matlab
-
-class TwoWheeledSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, theta]
- history_xs : list
- time history of state
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.xs = np.zeros(3)
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(3)]
- k1 = [0.0 for _ in range(3)]
- k2 = [0.0 for _ in range(3)]
- k3 = [0.0 for _ in range(3)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- print(self.xs)
-
- def _func_x_1(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.cos(y_3) * u_1
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = math.sin(y_3) * u_1
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- y_dot = u_2
- return y_dot
-
-def main():
- dt = 0.05
- simulation_time = 10 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- # lineared car system
- V = 5.0
- Ad = np.array([[1., V * dt], [0., 1.]])
- Bd = np.array([[0.], [1. * dt]])
-
- C = np.eye(2)
- D = np.zeros((2, 1))
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([5., 0., 0.])
- init_xs_follow = np.array([0., 0., 0.])
- lead_car = TwoWheeledSystem(init_states=init_xs_lead)
- follow_car = TwoWheeledSystem(init_states=init_xs_follow)
-
- # create system
- # sysc = matlab.ss(A, B, C, D)
- # discrete system
- # sysd = matlab.c2d(sysc, dt)
-
- # evaluation function weight
- Q = np.diag([1., 1.])
- R = np.diag([5.])
- pre_step = 15
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- lead_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- follow_controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([30 * dt]), dt_input_lower=np.array([-30 * dt]),
- input_upper=np.array([30.]), input_lower=np.array([-30.]))
-
- lead_controller.initialize_controller()
- follow_controller.initialize_controller()
-
- # reference
- lead_reference = np.array([[0., 0.] for _ in range(pre_step)]).flatten()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- # make lead car's move
- if i > int(iteration_num / 3):
- lead_reference = np.array([[4., 0.] for _ in range(pre_step)]).flatten()
-
- lead_states = lead_car.xs
- lead_opt_u = lead_controller.calc_input(lead_states[1:], lead_reference)
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- # make follow car
- follow_reference = np.array([lead_states[1:] for _ in range(pre_step)]).flatten()
- follow_states = follow_car.xs
-
- follow_opt_u = follow_controller.calc_input(follow_states[1:], follow_reference)
- follow_opt_u = np.hstack((np.array([V]), follow_opt_u))
-
- lead_car.update_state(lead_opt_u, dt=dt)
- follow_car.update_state(follow_opt_u, dt=dt)
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- follow_history_states = np.array(follow_car.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
-
- animdrawer = AnimDrawer([lead_history_states, follow_history_states])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/main_example.py b/mpc/basic/main_example.py
deleted file mode 100644
index b768a21..0000000
--- a/mpc/basic/main_example.py
+++ /dev/null
@@ -1,188 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_xs : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- D : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
- # print("xs = {0}".format(self.xs))
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
-
-def main():
- dt = 0.05
- simulation_time = 30 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- print(Ad)
- print(Bd)
- input()
-
- # evaluation function weight
- Q = np.diag([1., 1., 1., 1.])
- R = np.diag([1., 1.])
- pre_step = 10
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
- states = plant.xs
- opt_u = controller.calc_input(states, reference)
- plant.update_state(opt_u, dt=dt)
-
- history_states = np.array(plant.history_xs)
-
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 0])
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 1])
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 2])
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states[:, 3])
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us = np.array(controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 0])
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us[:, 1])
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_cvxopt.py b/mpc/basic/mpc_func_with_cvxopt.py
deleted file mode 100644
index 4e04736..0000000
--- a/mpc/basic/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,256 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/mpc_func_with_scipy.py b/mpc/basic/mpc_func_with_scipy.py
deleted file mode 100644
index 54ef3c9..0000000
--- a/mpc/basic/mpc_func_with_scipy.py
+++ /dev/null
@@ -1,262 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from scipy.optimize import minimize
-from scipy.optimize import LinearConstraint
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error) )
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- def optimized_func(dt_us):
- """
- """
- temp_dt_us = np.array([dt_us[i] for i in range(self.input_size * self.pre_step)])
-
- return (np.dot(temp_dt_us, np.dot(H, temp_dt_us.reshape(-1, 1))) - np.dot(G.T, temp_dt_us.reshape(-1, 1)))[0]
-
- # constraint
- lb = np.array([-np.inf for _ in range(len(ub))])
- linear_cons = LinearConstraint(A, lb, ub)
-
- init_dt_us = np.zeros(self.input_size * self.pre_step)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = minimize(optimized_func, init_dt_us, constraints=[linear_cons])
-
- opt_dt_us = opt_result.x
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
\ No newline at end of file
diff --git a/mpc/basic/test_compare_methods.py b/mpc/basic/test_compare_methods.py
deleted file mode 100644
index 5ddaea4..0000000
--- a/mpc/basic/test_compare_methods.py
+++ /dev/null
@@ -1,211 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from mpc_func_with_scipy import MpcController as MpcController_scipy
-from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from control import matlab
-
-class FirstOrderSystem():
- """FirstOrderSystemWithStates
-
- Attributes
- -----------
- states : float
- system states
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- history_state : list
- time history of state
- """
- def __init__(self, A, B, C, D=None, init_states=None):
- """
- Parameters
- -----------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- control matrix
- C : numpy.ndarray
- observation matrix
- C : numpy.ndarray
- directly matrix
- init_state : float, optional
- initial state of system default is None
- history_xs : list
- time history of system states
- """
-
- self.A = A
- self.B = B
- self.C = C
-
- if D is not None:
- self.D = D
-
- self.xs = np.zeros(self.A.shape[0])
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
-
- def update_state(self, u, dt=0.01):
- """calculating input
- Parameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- temp_x = self.xs.reshape(-1, 1)
- temp_u = u.reshape(-1, 1)
-
- # solve Runge-Kutta
- k0 = dt * (np.dot(self.A, temp_x) + np.dot(self.B, temp_u))
- k1 = dt * (np.dot(self.A, temp_x + k0/2.) + np.dot(self.B, temp_u))
- k2 = dt * (np.dot(self.A, temp_x + k1/2.) + np.dot(self.B, temp_u))
- k3 = dt * (np.dot(self.A, temp_x + k2) + np.dot(self.B, temp_u))
-
- self.xs += ((k0 + 2 * k1 + 2 * k2 + k3) / 6.).flatten()
-
- # for oylar
- # self.xs += k0.flatten()
-
- # print("xs = {0}".format(self.xs))
- # a = input()
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.history_xs)
-
-def main():
- dt = 0.05
- simulation_time = 50 # in seconds
- iteration_num = int(simulation_time / dt)
-
- # you must be care about this matrix
- # these A and B are for continuos system if you want to use discret system matrix please skip this step
- tau = 0.63
- A = np.array([[-1./tau, 0., 0., 0.],
- [0., -1./tau, 0., 0.],
- [1., 0., 0., 0.],
- [0., 1., 0., 0.]])
- B = np.array([[1./tau, 0.],
- [0., 1./tau],
- [0., 0.],
- [0., 0.]])
-
- C = np.eye(4)
- D = np.zeros((4, 2))
-
- # make simulator with coninuous matrix
- init_xs = np.array([0., 0., 0., 0.])
- plant_cvxopt = FirstOrderSystem(A, B, C, init_states=init_xs)
- plant_scipy = FirstOrderSystem(A, B, C, init_states=init_xs)
-
- # create system
- sysc = matlab.ss(A, B, C, D)
- # discrete system
- sysd = matlab.c2d(sysc, dt)
-
- Ad = sysd.A
- Bd = sysd.B
-
- # evaluation function weight
- Q = np.diag([1., 1., 10., 10.])
- R = np.diag([0.01, 0.01])
- pre_step = 5
-
- # make controller with discreted matrix
- # please check the solver, if you want to use the scipy, set the MpcController_scipy
- controller_cvxopt = MpcController_cvxopt(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_scipy = MpcController_scipy(Ad, Bd, Q, R, pre_step,
- dt_input_upper=np.array([0.25 * dt, 0.25 * dt]), dt_input_lower=np.array([-0.5 * dt, -0.5 * dt]),
- input_upper=np.array([1. ,3.]), input_lower=np.array([-1., -3.]))
-
- controller_cvxopt.initialize_controller()
- controller_scipy.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
- reference = np.array([[0., 0., -5., 7.5] for _ in range(pre_step)]).flatten()
-
- states_cvxopt = plant_cvxopt.xs
- states_scipy = plant_scipy.xs
-
- opt_u_cvxopt = controller_cvxopt.calc_input(states_cvxopt, reference)
- opt_u_scipy = controller_scipy.calc_input(states_scipy, reference)
-
- plant_cvxopt.update_state(opt_u_cvxopt)
- plant_scipy.update_state(opt_u_scipy)
-
- history_states_cvxopt = np.array(plant_cvxopt.history_xs)
- history_states_scipy = np.array(plant_scipy.history_xs)
-
- time_history_fig = plt.figure(dpi=75)
- x_fig = time_history_fig.add_subplot(411)
- y_fig = time_history_fig.add_subplot(412)
- v_x_fig = time_history_fig.add_subplot(413)
- v_y_fig = time_history_fig.add_subplot(414)
-
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 0], label="cvxopt")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 0], label="scipy", linestyle="dashdot")
- v_x_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_x_fig.set_xlabel("time [s]")
- v_x_fig.set_ylabel("v_x")
- v_x_fig.legend()
-
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 1], label="cvxopt")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 1], label="scipy", linestyle="dashdot")
- v_y_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- v_y_fig.set_xlabel("time [s]")
- v_y_fig.set_ylabel("v_y")
- v_y_fig.legend()
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 2], label="cvxopt")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 2], label="scipy", linestyle="dashdot")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), [-5. for _ in range(iteration_num+1)], linestyle="dashed")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_cvxopt[:, 3], label ="cvxopt")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), history_states_scipy[:, 3], label="scipy", linestyle="dashdot")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [7.5 for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- time_history_fig.tight_layout()
- plt.show()
-
- history_us_cvxopt = np.array(controller_cvxopt.history_us)
- history_us_scipy = np.array(controller_scipy.history_us)
-
- input_history_fig = plt.figure(dpi=75)
- u_1_fig = input_history_fig.add_subplot(211)
- u_2_fig = input_history_fig.add_subplot(212)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 0], label="cvxopt")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 0], label="scipy", linestyle="dashdot")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_x")
- u_1_fig.legend()
-
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_cvxopt[:, 1], label="cvxopt")
- u_2_fig.plot(np.arange(0, simulation_time+0.01, dt), history_us_scipy[:, 1], label="scipy", linestyle="dashdot")
- u_2_fig.set_xlabel("time [s]")
- u_2_fig.set_ylabel("u_y")
- u_2_fig.legend()
- input_history_fig.tight_layout()
- plt.show()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/README.md b/mpc/extend/README.md
deleted file mode 100644
index e926aa5..0000000
--- a/mpc/extend/README.md
+++ /dev/null
@@ -1,41 +0,0 @@
-# Model Predictive Control for Vehicle model
-This program is for controlling the vehicle model.
-I implemented the steering control for vehicle by using Model Predictive Control.
-
-# Model
-Usually, the vehicle model is expressed by extremely complicated nonlinear equation.
-Acoording to reference 1, I used the simple model as shown in following equation.
-
- -
-
-
- -
-# Usage
-
-```
-$ python main_track.py
-```
-
-# Reference
-- 1. https://qiita.com/taka_horibe/items/47f86e02e2db83b0c570#%E8%BB%8A%E4%B8%A1%E3%81%AE%E8%BB%8C%E9%81%93%E8%BF%BD%E5%BE%93%E5%95%8F%E9%A1%8C%E9%9D%9E%E7%B7%9A%E5%BD%A2%E3%81%AB%E9%81%A9%E7%94%A8%E3%81%99%E3%82%8B (Japanese)
diff --git a/mpc/extend/animation.py b/mpc/extend/animation.py
deleted file mode 100755
index a085b5a..0000000
--- a/mpc/extend/animation.py
+++ /dev/null
@@ -1,324 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.lead_car_history_state = objects[0]
- self.lead_car_history_predict_state = objects[1]
- self.traj = objects[2]
- self.history_traj_ref = objects[3]
- self.history_angle_ref = objects[4]
-
- self.history_xs = [self.lead_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
- self.predict_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 5
- HIGH_MARGIN = 5
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], ".", color="m")
- self.traj_imgs.append(temp_img)
-
- # predict
- for _ in range(2 * len(self.history_angle_ref[0])):
- temp_img, = self.axis.plot([],[], color="g", linewidth=0.5) # point
- # temp_img, = self.axis.plot([],[], ".", color="g", linewidth=0.5) # point
- self.predict_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs, self.predict_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 5.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # all traj_ref
- self.traj_imgs[1].set_data(self.traj[0, :], self.traj[1, :])
-
- # traj_ref
- # self.traj_imgs[2].set_data(self.history_traj_ref[i][0, :], self.history_traj_ref[i][1, :])
-
- def _draw_prediction(self, i):
- """draw prediction
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
-
- for j in range(0, len(self.history_angle_ref[0]), 4):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y =\
- circle_make_with_angles(self.lead_car_history_predict_state[i][j, 0],
- self.lead_car_history_predict_state[i][j, 1], 1.,
- self.lead_car_history_predict_state[i][j, 2])
-
- self.predict_imgs[fix_j].set_data(object_x, object_y)
- self.predict_imgs[fix_j + 1].set_data(angle_x, angle_y)
\ No newline at end of file
diff --git a/mpc/extend/coordinate_trans.py b/mpc/extend/coordinate_trans.py
deleted file mode 100755
index 9cfa220..0000000
--- a/mpc/extend/coordinate_trans.py
+++ /dev/null
@@ -1,112 +0,0 @@
-import math
-import numpy as np
-import copy
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def coordinate_transformation_in_position(positions, base_positions):
- '''
- Transformation the coordinate in the positions
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_positions : numpy.ndarray
- this parameter is composed of x, y
- shoulg have (2, 1) shape
-
- Returns
- -------
- traslated_positions : numpy.ndarray, shape(2, N)
-
- '''
-
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- base_positions = np.array(base_positions)
- base_positions = base_positions.reshape(2, 1)
-
- translated_positions = positions - base_positions
-
- return translated_positions
-
-
-def coordinate_transformation_in_matrix_angles(positions, base_angles):
- '''
- Transformation the coordinate in the matrix angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- translated_positions = np.zeros_like(positions)
-
- for i in range(len(base_angles)):
- rot_matrix = [[np.cos(base_angles[i]), np.sin(base_angles[i])],
- [-1*np.sin(base_angles[i]), np.cos(base_angles[i])]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_position = np.dot(rot_matrix, positions[:, i].reshape(2, 1))
-
- translated_positions[:, i] = translated_position.flatten()
-
- return translated_positions.reshape(2, -1)
-
-# def coordinate_inv_transformation
-if __name__ == '__main__':
- positions_1 = np.array([[1.0], [2.0]])
- base_angle = 1.25
-
- translated_positions_1 = coordinate_transformation_in_angle(positions_1, base_angle)
- print(translated_positions_1)
-
diff --git a/mpc/extend/extended_MPC.py b/mpc/extend/extended_MPC.py
deleted file mode 100644
index c365aaf..0000000
--- a/mpc/extend/extended_MPC.py
+++ /dev/null
@@ -1,306 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-import cvxopt
-cvxopt.solvers.options['show_progress'] = False # not display
-
-class IterativeMpcController():
- """
- Attributes
- ------------
- Ad_s : list of numpy.ndarray
- system matrix
- Bd_s : list of numpy.ndarray
- input matrix
- W_D_s : list of numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, system_model, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- system_model : SystemModel class
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.Ad_s[0].shape[0]
- self.input_size = self.Bd_s[0].shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.Ad_s[0]]
-
- self.phi_mat = copy.deepcopy(self.Ad_s[0])
-
- for i in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.Ad_s[i + 1])
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- # print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.Bd_s[0])
- gammma_mat_temp = copy.deepcopy(self.Bd_s[0])
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.Bd_s[i + 1])
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- # print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- # print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- # print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- # print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- # print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D_s[0])
-
- for i in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D_s[i + 1]))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- # print("Qs = \n{0}".format(self.Qs))
- # print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- # print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- # print("F = \n{0}".format(self.F))
- # print("F1 = \n{0}".format(self.F1))
- # print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- # print("W = \n{0}".format(self.W))
- # print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_u : numpy.ndarray, shape(input_length, )
- optimal input
- all_opt_u : numpy.ndarray, shape(PREDICT_STEP, input_length)
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # calc all predit u
- all_opt_u = [copy.deepcopy(opt_u)]
- temp_u = copy.deepcopy(opt_u)
-
- for i in range(1, self.pre_step):
- temp_u += opt_dt_us[i * self.input_size: (i + 1) * self.input_size]
- all_opt_u.append(copy.deepcopy(temp_u))
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u, np.array(all_opt_u)
-
- def update_system_model(self, system_model):
- """update system model
- Parameters
- -----------
- system_model : SystemModel class
- """
-
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
-
- self.initialize_controller()
diff --git a/mpc/extend/func_curvature.py b/mpc/extend/func_curvature.py
deleted file mode 100644
index cdd99e6..0000000
--- a/mpc/extend/func_curvature.py
+++ /dev/null
@@ -1,182 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-import random
-
-from traj_func import make_sample_traj
-
-def calc_curvature(points):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape (2, 3)
- these points should follow subseqently
-
- Returns
- ----------
- curvature : float
- """
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.show()
- """
-
- return 1. / R
-
-def calc_curvatures(traj_ref, predict_step, num_skip):
- """
- Parameters
- -----------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- predict_step : int
- predict step
- num_skip : int
- skip_num
-
- Returns
- ----------
- angles : list
- curvature : list
- """
-
- angles = []
- curvatures = []
-
- for i in range(predict_step):
- # make pairs
- points = np.zeros((2, 3))
-
- points[:, 0] = traj_ref[:, i]
- points[:, 1] = traj_ref[:, i + num_skip]
- points[:, 2] = traj_ref[:, i + 2 * num_skip]
-
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- # calc R
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- # add
- diff = points[:, 2] - points[:, 0]
- angles.append(math.atan2(diff[1], diff[0]))
- curvatures.append(1. / R)
-
- # plot
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for x in np.arange(-5, 5, 0.01):
- plot_points_x.append(x)
- plot_points_y.append(x * math.tan(angles[-1]))
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.xlim(-1, 10)
- plt.ylim(-1, 2)
-
- plt.show()
- """
-
- return angles, curvatures
-
-def calc_ideal_vel(traj_ref, dt):
- """
- Parameters
- ------------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- dt : float
- sampling time of system
- """
- # end point and start point
- diff = traj_ref[:, -1] - traj_ref[:, 0]
- distance = np.sqrt(np.sum(diff**2))
-
- V = distance / (dt * traj_ref.shape[1])
-
- return V
-
-def main():
- """
- points = np.zeros((2, 3))
- points[:, 0] = np.array([1. + random.random(), random.random()])
-
- points[:, 1] = np.array([random.random(), 3 + random.random()])
-
- points[:, 2] = np.array([3 + random.random(), -3 + random.random()])
-
- calc_cuvature(points)
- """
-
- traj_ref_xs, traj_ref_ys = make_sample_traj(1000)
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- calc_curvatures(traj_ref[:, 10:10 + 15 + 100 * 2], 15, 100)
-
-
-if __name__ == "__main__":
- main()
-
-
-
-
-
diff --git a/mpc/extend/main_track.py b/mpc/extend/main_track.py
deleted file mode 100644
index f78413f..0000000
--- a/mpc/extend/main_track.py
+++ /dev/null
@@ -1,464 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-# from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from extended_MPC import IterativeMpcController
-from animation import AnimDrawer
-# from control import matlab
-from coordinate_trans import coordinate_transformation_in_angle, coordinate_transformation_in_position
-from traj_func import make_sample_traj
-from func_curvature import calc_curvatures, calc_ideal_vel
-
-class WheeledSystem():
- """SampleSystem, this is the simulator
- Kinematic model of car
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, phi, beta]
- history_xs : list
- time history of state
- tau : float
- time constant of tire
- FRONT_WHEEL_BASE : float
- REAR_WHEEL_BASE : float
- predict_xs :
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.NUM_STATE = 4
- self.xs = np.zeros(self.NUM_STATE)
-
- self.tau = 0.01
-
- self.FRONT_WHEELE_BASE = 1.0
- self.REAR_WHEELE_BASE = 1.0
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], self.xs[3], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., self.xs[3] + k0[3]/2, us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k1[0]/2., self.xs[1] + k1[1]/2., self.xs[2] + k1[2]/2., self.xs[3] + k1[3]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], self.xs[3] + k2[3], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- self.xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.xs)
-
- def predict_state(self, us, dt=0.01):
- """make predict state by using optimal input made by MPC
- Paramaters
- -----------
- us : array-like, shape(2, N)
- optimal input made by MPC
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
-
- xs = copy.deepcopy(self.xs)
- predict_xs = [copy.deepcopy(xs)]
-
- for i in range(us.shape[1]):
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(xs[0], xs[1], xs[2], xs[3], us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(xs[0] + k0[0]/2., xs[1] + k0[1]/2., xs[2] + k0[2]/2., xs[3] + k0[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(xs[0] + k1[0]/2., xs[1] + k1[1]/2., xs[2] + k1[2]/2., xs[3] + k1[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(xs[0] + k2[0], xs[1] + k2[1], xs[2] + k2[2], xs[3] + k2[3], us[0, i], us[1, i])
-
- xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- predict_xs.append(copy.deepcopy(xs))
-
- self.history_predict_xs.append(np.array(predict_xs))
-
- def _func_x_1(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.cos(y_3 + y_4)
- y_dot = u_1 * math.cos(y_3)
-
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.sin(y_3 + y_4)
- y_dot = u_1 * math.sin(y_3)
-
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 / self.REAR_WHEELE_BASE * math.sin(y_4)
- y_dot = u_1 * math.tan(y_4) / (self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
-
- return y_dot
-
- def _func_x_4(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """Ad, Bd, W_D, Q, R
- ParAd, Bd, W_D, Q, R
- ---Ad, Bd, W_D, Q, R
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = math.atan2(self.REAR_WHEELE_BASE * math.tan(u_2) ,self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
- y_dot = - 1. / self.tau * (y_4 - u_2)
-
- return y_dot
-
-class SystemModel():
- """
- Attributes
- -----------
- WHEEL_BASE : float
- wheel base of the car
- Ad_s : list
- list of system model matrix Ad
- Bd_s : list
- list of system model matrix Bd
- W_D_s : list
- list of system model matrix W_D_s
- Q : numpy.ndarray
- R : numpy.ndarray
- """
- def __init__(self, tau = 0.01, dt = 0.01):
- """
- Parameters
- -----------
- tau : time constant, optional
- dt : sampling time, optional
- """
- self.dt = dt
- self.tau = tau
- self.WHEEL_BASE = 2.2
-
- self.Ad_s = []
- self.Bd_s = []
- self.W_D_s = []
-
- def calc_predict_sytem_model(self, V, curvatures, predict_step):
- """
- calc next predict systemo models
- V : float
- current speed of car
- curvatures : list
- this is the next curvature's list
- predict_step : int
- predict step of MPC
- """
- for i in range(predict_step):
- delta_r = math.atan2(self.WHEEL_BASE, 1. / curvatures[i])
-
- A12 = (V / self.WHEEL_BASE) / (math.cos(delta_r)**2)
- A22 = (1. - 1. / self.tau * self.dt)
-
- Ad = np.array([[1., V * self.dt, 0.],
- [0., 1., A12 * self.dt],
- [0., 0., A22]])
-
- Bd = np.array([[0.], [0.], [1. / self.tau]]) * self.dt
-
- # -v*curvature + v/L*(tan(delta_r)-delta_r*cos_delta_r_squared_inv);
- # W_D_0 = V / self.WHEEL_BASE * (delta_r / (math.cos(delta_r)**2)
- W_D_0 = -V * curvatures[i] + (V / self.WHEEL_BASE) * (math.tan(delta_r) - delta_r / (math.cos(delta_r)**2))
-
- W_D = np.array([[0.], [W_D_0], [0.]]) * self.dt
-
- self.Ad_s.append(Ad)
- self.Bd_s.append(Bd)
- self.W_D_s.append(W_D)
-
- # return self.Ad_s, self.Bd_s, self.W_D_s
-
-def search_nearest_point(points, base_point):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape is (2, N)
- base_point : numpy.ndarray, shape is (2, 1)
-
- Returns
- -------
- nearest_index :
- nearest_point :
- """
- distance_mat = np.sqrt(np.sum((points - base_point)**2, axis=0))
-
- index_min = np.argmin(distance_mat)
-
- return index_min, points[:, index_min]
-
-
-def main():
- # parameters
- dt = 0.01
- simulation_time = 20 # in seconds
- PREDICT_STEP = 30
- iteration_num = int(simulation_time / dt)
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([0., 0., math.pi/5, 0.])
- lead_car = WheeledSystem(init_states=init_xs_lead)
-
- # make system model
- lead_car_system_model = SystemModel()
-
- # reference
- history_traj_ref = []
- history_angle_ref = []
- traj_ref_xs, traj_ref_ys = make_sample_traj(int(simulation_time/dt))
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # get traj's curvature
- NUM_SKIP = 3
- MARGIN = 50
- angles, curvatures = calc_curvatures(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save traj ref
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # print(history_traj_ref)
- # input()
-
- # evaluation function weight
- Q = np.diag([1e2, 1., 1e3])
- R = np.diag([1e2])
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # make controller with discreted matrix
- lead_controller = IterativeMpcController(lead_car_system_model, Q, R, PREDICT_STEP,
- dt_input_upper=np.array([1 * dt]), dt_input_lower=np.array([-1 * dt]),
- input_upper=np.array([1.]), input_lower=np.array([-1.]))
-
-
- # initialize
- lead_controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
-
- ## lead
- # world traj
- lead_states = lead_car.xs
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # end check
- if len(traj_ref_ys) <= index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN:
- print("break")
- break
-
- # get traj's curvature
- angles, curvatures = calc_curvatures(traj_ref[:, index_min+MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # transformation
- # car
- relative_car_position = coordinate_transformation_in_position(lead_states[:2].reshape(2, 1), nearest_point)
- relative_car_position = coordinate_transformation_in_angle(relative_car_position, angles[0])
-
- relative_car_angle = lead_states[2] - angles[0]
- relative_car_state = np.hstack((relative_car_position[1], relative_car_angle, lead_states[-1]))
-
- # traj_ref
- relative_traj = coordinate_transformation_in_position(traj_ref[:, index_min:index_min + PREDICT_STEP], nearest_point)
- relative_traj = coordinate_transformation_in_angle(relative_traj, angles[0])
- relative_ref_angle = np.array(angles) - angles[0]
-
- # make ref
- lead_reference = np.array([[relative_traj[1, -1], relative_ref_angle[-1], 0.] for i in range(PREDICT_STEP)]).flatten()
-
- print("relative car state = {}".format(relative_car_state))
- print("nearest point = {}".format(nearest_point))
- # input()
-
- # update system matrix
- lead_controller.update_system_model(lead_car_system_model)
-
- lead_opt_u, all_opt_u = lead_controller.calc_input(relative_car_state, lead_reference)
-
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- all_opt_u = np.stack((np.ones(PREDICT_STEP)*V, all_opt_u.flatten()))
-
- print("opt_u = {}".format(lead_opt_u))
- print("all_opt_u = {}".format(all_opt_u))
-
- # predict
- lead_car.predict_state(all_opt_u, dt=dt)
-
- # update
- lead_car.update_state(lead_opt_u, dt=dt)
-
- # print(lead_car.history_predict_xs)
- # input()
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- lead_history_predict_states = lead_car.history_predict_xs
-
- """
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
- """
-
- animdrawer = AnimDrawer([lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/mpc_func_with_cvxopt.py b/mpc/extend/mpc_func_with_cvxopt.py
deleted file mode 100644
index a46d2d2..0000000
--- a/mpc/extend/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,304 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, W_D, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.W_D = np.array(W_D)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D)
-
- for _ in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
-
- def update_system_model(self, A, B, W_D):
- """update system model
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- """
-
- self.A = A
- self.B = B
- self.W_D = W_D
-
- self.initialize_controller()
diff --git a/mpc/extend/traj_func.py b/mpc/extend/traj_func.py
deleted file mode 100644
index 8f5ce18..0000000
--- a/mpc/extend/traj_func.py
+++ /dev/null
@@ -1,31 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-def make_sample_traj(NUM, dt=0.01, a=30.):
- """
- make sample trajectory
- Parameters
- ------------
- NUM : int
- dt : float
- a : float
-
- Returns
- ----------
- traj_xs : list
- traj_ys : list
- """
- DELAY = 2.
- traj_xs = []
- traj_ys = []
-
- for i in range(NUM):
- traj_xs.append(i * 0.1)
- traj_ys.append(a * math.sin(dt * i / DELAY))
-
- plt.plot(traj_xs, traj_ys)
- plt.show()
-
- return traj_xs, traj_ys
-
diff --git a/nmpc/cgmres/README.md b/nmpc/cgmres/README.md
deleted file mode 100644
index a46901c..0000000
--- a/nmpc/cgmres/README.md
+++ /dev/null
@@ -1,79 +0,0 @@
-# CGMRES method of Nonlinear Model Predictive Control
-This program is about Continuous gmres method for NMPC
-Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
-By using CGMRES, we can pass the calculating step and get the optimal input quickly.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
-
-
-# Usage
-
-```
-$ python main_track.py
-```
-
-# Reference
-- 1. https://qiita.com/taka_horibe/items/47f86e02e2db83b0c570#%E8%BB%8A%E4%B8%A1%E3%81%AE%E8%BB%8C%E9%81%93%E8%BF%BD%E5%BE%93%E5%95%8F%E9%A1%8C%E9%9D%9E%E7%B7%9A%E5%BD%A2%E3%81%AB%E9%81%A9%E7%94%A8%E3%81%99%E3%82%8B (Japanese)
diff --git a/mpc/extend/animation.py b/mpc/extend/animation.py
deleted file mode 100755
index a085b5a..0000000
--- a/mpc/extend/animation.py
+++ /dev/null
@@ -1,324 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import matplotlib.animation as ani
-import matplotlib.font_manager as fon
-import sys
-import math
-
-# default setting of figures
-plt.rcParams["mathtext.fontset"] = 'stix' # math fonts
-plt.rcParams['xtick.direction'] = 'in' # x axis in
-plt.rcParams['ytick.direction'] = 'in' # y axis in
-plt.rcParams["font.size"] = 10
-plt.rcParams['axes.linewidth'] = 1.0 # axis line width
-plt.rcParams['axes.grid'] = True # make grid
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def square_make_with_angles(center_x, center_y, size, angle):
- '''
- Create square matrix with angle line matrix(2D)
-
- Parameters
- -------
- center_x : float in meters
- the center x position of the square
- center_y : float in meters
- the center y position of the square
- size : float in meters
- the square's half-size
- angle : float in radians
-
- Returns
- -------
- square xs : numpy.ndarray
- lenght is 5 (counterclockwise from right-up)
- square ys : numpy.ndarray
- length is 5 (counterclockwise from right-up)
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- # start with the up right points
- # create point in counterclockwise
- square_xys = np.array([[size, 0.5 * size], [-size, 0.5 * size], [-size, -0.5 * size], [size, -0.5 * size], [size, 0.5 * size]])
- trans_points = coordinate_transformation_in_angle(square_xys.T, -angle) # this is inverse type
- trans_points += np.array([[center_x], [center_y]])
-
- square_xs = trans_points[0, :]
- square_ys = trans_points[1, :]
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * size]
- angle_line_ys = [center_y, center_y + math.sin(angle) * size]
-
- return square_xs, square_ys, np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-def circle_make_with_angles(center_x, center_y, radius, angle):
- '''
- Create circle matrix with angle line matrix
-
- Parameters
- -------
- center_x : float
- the center x position of the circle
- center_y : float
- the center y position of the circle
- radius : float
- angle : float [rad]
-
- Returns
- -------
- circle xs : numpy.ndarray
- circle ys : numpy.ndarray
- angle line xs : numpy.ndarray
- angle line ys : numpy.ndarray
- '''
-
- point_num = 100 # 分解能
-
- circle_xs = []
- circle_ys = []
-
- for i in range(point_num + 1):
- circle_xs.append(center_x + radius * math.cos(i*2*math.pi/point_num))
- circle_ys.append(center_y + radius * math.sin(i*2*math.pi/point_num))
-
- angle_line_xs = [center_x, center_x + math.cos(angle) * radius]
- angle_line_ys = [center_y, center_y + math.sin(angle) * radius]
-
- return np.array(circle_xs), np.array(circle_ys), np.array(angle_line_xs), np.array(angle_line_ys)
-
-
-class AnimDrawer():
- """create animation of path and robot
-
- Attributes
- ------------
- cars :
- anim_fig : figure of matplotlib
- axis : axis of matplotlib
-
- """
- def __init__(self, objects):
- """
- Parameters
- ------------
- objects : list of objects
-
- Notes
- ---------
- lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref
- """
- self.lead_car_history_state = objects[0]
- self.lead_car_history_predict_state = objects[1]
- self.traj = objects[2]
- self.history_traj_ref = objects[3]
- self.history_angle_ref = objects[4]
-
- self.history_xs = [self.lead_car_history_state[:, 0]]
- self.history_ys = [self.lead_car_history_state[:, 1]]
- self.history_ths = [self.lead_car_history_state[:, 2]]
-
- # setting up figure
- self.anim_fig = plt.figure(dpi=150)
- self.axis = self.anim_fig.add_subplot(111)
-
- # imgs
- self.car_imgs = []
- self.traj_imgs = []
- self.predict_imgs = []
-
- def draw_anim(self, interval=50):
- """draw the animation and save
-
- Parameteres
- -------------
- interval : int, optional
- animation's interval time, you should link the sampling time of systems
- default is 50 [ms]
- """
- self._set_axis()
- self._set_img()
-
- self.skip_num = 1
- frame_num = int((len(self.history_xs[0])-1) / self.skip_num)
-
- animation = ani.FuncAnimation(self.anim_fig, self._update_anim, interval=interval, frames=frame_num)
-
- # self.axis.legend()
- print('save_animation?')
- shuold_save_animation = int(input())
-
- if shuold_save_animation:
- print('animation_number?')
- num = int(input())
- animation.save('animation_{0}.mp4'.format(num), writer='ffmpeg')
- # animation.save("Sample.gif", writer = 'imagemagick') # gif保存
-
- plt.show()
-
- def _set_axis(self):
- """ initialize the animation axies
- """
- # (1) set the axis name
- self.axis.set_xlabel(r'$\it{x}$ [m]')
- self.axis.set_ylabel(r'$\it{y}$ [m]')
- self.axis.set_aspect('equal', adjustable='box')
-
- LOW_MARGIN = 5
- HIGH_MARGIN = 5
-
- self.axis.set_xlim(np.min(self.history_xs) - LOW_MARGIN, np.max(self.history_xs) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys) - LOW_MARGIN, np.max(self.history_ys) + HIGH_MARGIN)
-
- def _set_img(self):
- """ initialize the imgs of animation
- this private function execute the make initial imgs for animation
- """
- # object imgs
- obj_color_list = ["k", "k", "m", "m"]
- obj_styles = ["solid", "solid", "solid", "solid"]
-
- for i in range(len(obj_color_list)):
- temp_img, = self.axis.plot([], [], color=obj_color_list[i], linestyle=obj_styles[i])
- self.car_imgs.append(temp_img)
-
- traj_color_list = ["k", "b"]
-
- for i in range(len(traj_color_list)):
- temp_img, = self.axis.plot([],[], color=traj_color_list[i], linestyle="dashed")
- self.traj_imgs.append(temp_img)
-
- temp_img, = self.axis.plot([],[], ".", color="m")
- self.traj_imgs.append(temp_img)
-
- # predict
- for _ in range(2 * len(self.history_angle_ref[0])):
- temp_img, = self.axis.plot([],[], color="g", linewidth=0.5) # point
- # temp_img, = self.axis.plot([],[], ".", color="g", linewidth=0.5) # point
- self.predict_imgs.append(temp_img)
-
- def _update_anim(self, i):
- """the update animation
- this function should be used in the animation functions
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
-
- Returns
- -----------
- object_imgs : list of img
- traj_imgs : list of img
- """
- i = int(i * self.skip_num)
-
- # self._draw_set_axis(i)
- self._draw_car(i)
- self._draw_traj(i)
- # self._draw_prediction(i)
-
- return self.car_imgs, self.traj_imgs, self.predict_imgs,
-
- def _draw_set_axis(self, i):
- """
- """
- # (2) set the xlim and ylim
- LOW_MARGIN = 20
- HIGH_MARGIN = 20
- OVER_LOOK = 50
- self.axis.set_xlim(np.min(self.history_xs[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_xs[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
- self.axis.set_ylim(np.min(self.history_ys[0][i : i + OVER_LOOK]) - LOW_MARGIN, np.max(self.history_ys[0][i : i + OVER_LOOK]) + HIGH_MARGIN)
-
- def _draw_car(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # cars
- object_x, object_y, angle_x, angle_y = square_make_with_angles(self.history_xs[0][i],
- self.history_ys[0][i],
- 5.0,
- self.history_ths[0][i])
-
- self.car_imgs[0].set_data([object_x, object_y])
- self.car_imgs[1].set_data([angle_x, angle_y])
-
- def _draw_traj(self, i):
- """
- This private function is just divided thing of
- the _update_anim to see the code more clear
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
- # car
- self.traj_imgs[0].set_data(self.history_xs[0][:i], self.history_ys[0][:i])
-
- # all traj_ref
- self.traj_imgs[1].set_data(self.traj[0, :], self.traj[1, :])
-
- # traj_ref
- # self.traj_imgs[2].set_data(self.history_traj_ref[i][0, :], self.history_traj_ref[i][1, :])
-
- def _draw_prediction(self, i):
- """draw prediction
-
- Parameters
- ------------
- i : int
- time step of the animation
- the sampling time should be related to the sampling time of system
- """
-
- for j in range(0, len(self.history_angle_ref[0]), 4):
- fix_j = j * 2
- object_x, object_y, angle_x, angle_y =\
- circle_make_with_angles(self.lead_car_history_predict_state[i][j, 0],
- self.lead_car_history_predict_state[i][j, 1], 1.,
- self.lead_car_history_predict_state[i][j, 2])
-
- self.predict_imgs[fix_j].set_data(object_x, object_y)
- self.predict_imgs[fix_j + 1].set_data(angle_x, angle_y)
\ No newline at end of file
diff --git a/mpc/extend/coordinate_trans.py b/mpc/extend/coordinate_trans.py
deleted file mode 100755
index 9cfa220..0000000
--- a/mpc/extend/coordinate_trans.py
+++ /dev/null
@@ -1,112 +0,0 @@
-import math
-import numpy as np
-import copy
-
-def coordinate_transformation_in_angle(positions, base_angle):
- '''
- Transformation the coordinate in the angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
-
- rot_matrix = [[np.cos(base_angle), np.sin(base_angle)],
- [-1*np.sin(base_angle), np.cos(base_angle)]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_positions = np.dot(rot_matrix, positions)
-
- return translated_positions
-
-def coordinate_transformation_in_position(positions, base_positions):
- '''
- Transformation the coordinate in the positions
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_positions : numpy.ndarray
- this parameter is composed of x, y
- shoulg have (2, 1) shape
-
- Returns
- -------
- traslated_positions : numpy.ndarray, shape(2, N)
-
- '''
-
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- base_positions = np.array(base_positions)
- base_positions = base_positions.reshape(2, 1)
-
- translated_positions = positions - base_positions
-
- return translated_positions
-
-
-def coordinate_transformation_in_matrix_angles(positions, base_angles):
- '''
- Transformation the coordinate in the matrix angle
-
- Parameters
- -------
- positions : numpy.ndarray
- this parameter is composed of xs, ys
- should have (2, N) shape
- base_angle : float [rad]
-
- Returns
- -------
- traslated_positions : numpy.ndarray
- the shape is (2, N)
-
- '''
- if positions.shape[0] != 2:
- raise ValueError('the input data should have (2, N)')
-
- positions = np.array(positions)
- positions = positions.reshape(2, -1)
- translated_positions = np.zeros_like(positions)
-
- for i in range(len(base_angles)):
- rot_matrix = [[np.cos(base_angles[i]), np.sin(base_angles[i])],
- [-1*np.sin(base_angles[i]), np.cos(base_angles[i])]]
-
- rot_matrix = np.array(rot_matrix)
-
- translated_position = np.dot(rot_matrix, positions[:, i].reshape(2, 1))
-
- translated_positions[:, i] = translated_position.flatten()
-
- return translated_positions.reshape(2, -1)
-
-# def coordinate_inv_transformation
-if __name__ == '__main__':
- positions_1 = np.array([[1.0], [2.0]])
- base_angle = 1.25
-
- translated_positions_1 = coordinate_transformation_in_angle(positions_1, base_angle)
- print(translated_positions_1)
-
diff --git a/mpc/extend/extended_MPC.py b/mpc/extend/extended_MPC.py
deleted file mode 100644
index c365aaf..0000000
--- a/mpc/extend/extended_MPC.py
+++ /dev/null
@@ -1,306 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-import cvxopt
-cvxopt.solvers.options['show_progress'] = False # not display
-
-class IterativeMpcController():
- """
- Attributes
- ------------
- Ad_s : list of numpy.ndarray
- system matrix
- Bd_s : list of numpy.ndarray
- input matrix
- W_D_s : list of numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, system_model, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- system_model : SystemModel class
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.Ad_s[0].shape[0]
- self.input_size = self.Bd_s[0].shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
- """
- A_factorials = [self.Ad_s[0]]
-
- self.phi_mat = copy.deepcopy(self.Ad_s[0])
-
- for i in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.Ad_s[i + 1])
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- # print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.Bd_s[0])
- gammma_mat_temp = copy.deepcopy(self.Bd_s[0])
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.Bd_s[i + 1])
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- # print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- # print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- # print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- # print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- # print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D_s[0])
-
- for i in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D_s[i + 1]))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- # print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- # print("Qs = \n{0}".format(self.Qs))
- # print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- # print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- # print("F = \n{0}".format(self.F))
- # print("F1 = \n{0}".format(self.F1))
- # print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- # print("W = \n{0}".format(self.W))
- # print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_u : numpy.ndarray, shape(input_length, )
- optimal input
- all_opt_u : numpy.ndarray, shape(PREDICT_STEP, input_length)
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # calc all predit u
- all_opt_u = [copy.deepcopy(opt_u)]
- temp_u = copy.deepcopy(opt_u)
-
- for i in range(1, self.pre_step):
- temp_u += opt_dt_us[i * self.input_size: (i + 1) * self.input_size]
- all_opt_u.append(copy.deepcopy(temp_u))
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u, np.array(all_opt_u)
-
- def update_system_model(self, system_model):
- """update system model
- Parameters
- -----------
- system_model : SystemModel class
- """
-
- self.Ad_s = system_model.Ad_s
- self.Bd_s = system_model.Bd_s
- self.W_D_s = system_model.W_D_s
-
- self.initialize_controller()
diff --git a/mpc/extend/func_curvature.py b/mpc/extend/func_curvature.py
deleted file mode 100644
index cdd99e6..0000000
--- a/mpc/extend/func_curvature.py
+++ /dev/null
@@ -1,182 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-import random
-
-from traj_func import make_sample_traj
-
-def calc_curvature(points):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape (2, 3)
- these points should follow subseqently
-
- Returns
- ----------
- curvature : float
- """
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.show()
- """
-
- return 1. / R
-
-def calc_curvatures(traj_ref, predict_step, num_skip):
- """
- Parameters
- -----------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- predict_step : int
- predict step
- num_skip : int
- skip_num
-
- Returns
- ----------
- angles : list
- curvature : list
- """
-
- angles = []
- curvatures = []
-
- for i in range(predict_step):
- # make pairs
- points = np.zeros((2, 3))
-
- points[:, 0] = traj_ref[:, i]
- points[:, 1] = traj_ref[:, i + num_skip]
- points[:, 2] = traj_ref[:, i + 2 * num_skip]
-
- # Gradient 1
- diff = points[:, 0] - points[:, 1]
- Gradient_1 = -1. / (diff[1] / diff[0])
- # Gradient 2
- diff = points[:, 1] - points[:, 2]
- Gradient_2 = -1. / (diff[1] / diff[0])
-
- # middle point 1
- middle_point_1 = (points[:, 0] + points[:, 1]) / 2.
-
- # middle point 2
- middle_point_2 = (points[:, 1] + points[:, 2]) / 2.
-
- # calc center
- c_x = (middle_point_1[1] - middle_point_2[1] - middle_point_1[0] * Gradient_1 + middle_point_2[0] * Gradient_2) / (Gradient_2 - Gradient_1)
- c_y = middle_point_1[1] - (middle_point_1[0] - c_x) * Gradient_1
-
- # calc R
- R = math.sqrt((points[0, 0] - c_x)**2 + (points[1, 0] - c_y)**2)
-
- # add
- diff = points[:, 2] - points[:, 0]
- angles.append(math.atan2(diff[1], diff[0]))
- curvatures.append(1. / R)
-
- # plot
- """
- plt.scatter(points[0, :], points[1, :])
- plt.scatter(c_x, c_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for theta in np.arange(0, 2*math.pi, 0.01):
- plot_points_x.append(math.cos(theta)*R + c_x)
- plot_points_y.append(math.sin(theta)*R + c_y)
-
- plt.plot(plot_points_x, plot_points_y)
-
- plot_points_x = []
- plot_points_y = []
-
- for x in np.arange(-5, 5, 0.01):
- plot_points_x.append(x)
- plot_points_y.append(x * math.tan(angles[-1]))
-
- plt.plot(plot_points_x, plot_points_y)
-
- plt.xlim(-1, 10)
- plt.ylim(-1, 2)
-
- plt.show()
- """
-
- return angles, curvatures
-
-def calc_ideal_vel(traj_ref, dt):
- """
- Parameters
- ------------
- traj_ref : numpy.ndarray, shape (2, N)
- these points should follow subseqently
- dt : float
- sampling time of system
- """
- # end point and start point
- diff = traj_ref[:, -1] - traj_ref[:, 0]
- distance = np.sqrt(np.sum(diff**2))
-
- V = distance / (dt * traj_ref.shape[1])
-
- return V
-
-def main():
- """
- points = np.zeros((2, 3))
- points[:, 0] = np.array([1. + random.random(), random.random()])
-
- points[:, 1] = np.array([random.random(), 3 + random.random()])
-
- points[:, 2] = np.array([3 + random.random(), -3 + random.random()])
-
- calc_cuvature(points)
- """
-
- traj_ref_xs, traj_ref_ys = make_sample_traj(1000)
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- calc_curvatures(traj_ref[:, 10:10 + 15 + 100 * 2], 15, 100)
-
-
-if __name__ == "__main__":
- main()
-
-
-
-
-
diff --git a/mpc/extend/main_track.py b/mpc/extend/main_track.py
deleted file mode 100644
index f78413f..0000000
--- a/mpc/extend/main_track.py
+++ /dev/null
@@ -1,464 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-# from mpc_func_with_cvxopt import MpcController as MpcController_cvxopt
-from extended_MPC import IterativeMpcController
-from animation import AnimDrawer
-# from control import matlab
-from coordinate_trans import coordinate_transformation_in_angle, coordinate_transformation_in_position
-from traj_func import make_sample_traj
-from func_curvature import calc_curvatures, calc_ideal_vel
-
-class WheeledSystem():
- """SampleSystem, this is the simulator
- Kinematic model of car
-
- Attributes
- -----------
- xs : numpy.ndarray
- system states, [x, y, phi, beta]
- history_xs : list
- time history of state
- tau : float
- time constant of tire
- FRONT_WHEEL_BASE : float
- REAR_WHEEL_BASE : float
- predict_xs :
- """
- def __init__(self, init_states=None):
- """
- Palameters
- -----------
- init_state : float, optional, shape(3, )
- initial state of system default is None
- """
- self.NUM_STATE = 4
- self.xs = np.zeros(self.NUM_STATE)
-
- self.tau = 0.01
-
- self.FRONT_WHEELE_BASE = 1.0
- self.REAR_WHEELE_BASE = 1.0
-
- if init_states is not None:
- self.xs = copy.deepcopy(init_states)
-
- self.history_xs = [init_states]
- self.history_predict_xs = []
-
- def update_state(self, us, dt=0.01):
- """
- Palameters
- ------------
- u : numpy.ndarray
- inputs of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.xs[0], self.xs[1], self.xs[2], self.xs[3], us[0], us[1])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.xs[0] + k0[0]/2., self.xs[1] + k0[1]/2., self.xs[2] + k0[2]/2., self.xs[3] + k0[3]/2, us[0], us[1])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.xs[0] + k1[0]/2., self.xs[1] + k1[1]/2., self.xs[2] + k1[2]/2., self.xs[3] + k1[3]/2., us[0], us[1])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.xs[0] + k2[0], self.xs[1] + k2[1], self.xs[2] + k2[2], self.xs[3] + k2[3], us[0], us[1])
-
- self.xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- self.xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- self.xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- # save
- save_states = copy.deepcopy(self.xs)
- self.history_xs.append(save_states)
- # print(self.xs)
-
- def predict_state(self, us, dt=0.01):
- """make predict state by using optimal input made by MPC
- Paramaters
- -----------
- us : array-like, shape(2, N)
- optimal input made by MPC
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
-
- xs = copy.deepcopy(self.xs)
- predict_xs = [copy.deepcopy(xs)]
-
- for i in range(us.shape[1]):
- k0 = [0.0 for _ in range(self.NUM_STATE)]
- k1 = [0.0 for _ in range(self.NUM_STATE)]
- k2 = [0.0 for _ in range(self.NUM_STATE)]
- k3 = [0.0 for _ in range(self.NUM_STATE)]
-
- functions = [self._func_x_1, self._func_x_2, self._func_x_3, self._func_x_4]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(xs[0], xs[1], xs[2], xs[3], us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(xs[0] + k0[0]/2., xs[1] + k0[1]/2., xs[2] + k0[2]/2., xs[3] + k0[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(xs[0] + k1[0]/2., xs[1] + k1[1]/2., xs[2] + k1[2]/2., xs[3] + k1[3]/2., us[0, i], us[1, i])
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(xs[0] + k2[0], xs[1] + k2[1], xs[2] + k2[2], xs[3] + k2[3], us[0, i], us[1, i])
-
- xs[0] += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- xs[1] += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
- xs[2] += (k0[2] + 2. * k1[2] + 2. * k2[2] + k3[2]) / 6.
- xs[3] += (k0[3] + 2. * k1[3] + 2. * k2[3] + k3[3]) / 6.
-
- predict_xs.append(copy.deepcopy(xs))
-
- self.history_predict_xs.append(np.array(predict_xs))
-
- def _func_x_1(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.cos(y_3 + y_4)
- y_dot = u_1 * math.cos(y_3)
-
- return y_dot
-
- def _func_x_2(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 * math.sin(y_3 + y_4)
- y_dot = u_1 * math.sin(y_3)
-
- return y_dot
-
- def _func_x_3(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = u_1 / self.REAR_WHEELE_BASE * math.sin(y_4)
- y_dot = u_1 * math.tan(y_4) / (self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
-
- return y_dot
-
- def _func_x_4(self, y_1, y_2, y_3, y_4, u_1, u_2):
- """Ad, Bd, W_D, Q, R
- ParAd, Bd, W_D, Q, R
- ---Ad, Bd, W_D, Q, R
- y_1 : float
- y_2 : float
- y_3 : float
- u_1 : float
- system input
- u_2 : float
- system input
- """
- # y_dot = math.atan2(self.REAR_WHEELE_BASE * math.tan(u_2) ,self.REAR_WHEELE_BASE + self.FRONT_WHEELE_BASE)
- y_dot = - 1. / self.tau * (y_4 - u_2)
-
- return y_dot
-
-class SystemModel():
- """
- Attributes
- -----------
- WHEEL_BASE : float
- wheel base of the car
- Ad_s : list
- list of system model matrix Ad
- Bd_s : list
- list of system model matrix Bd
- W_D_s : list
- list of system model matrix W_D_s
- Q : numpy.ndarray
- R : numpy.ndarray
- """
- def __init__(self, tau = 0.01, dt = 0.01):
- """
- Parameters
- -----------
- tau : time constant, optional
- dt : sampling time, optional
- """
- self.dt = dt
- self.tau = tau
- self.WHEEL_BASE = 2.2
-
- self.Ad_s = []
- self.Bd_s = []
- self.W_D_s = []
-
- def calc_predict_sytem_model(self, V, curvatures, predict_step):
- """
- calc next predict systemo models
- V : float
- current speed of car
- curvatures : list
- this is the next curvature's list
- predict_step : int
- predict step of MPC
- """
- for i in range(predict_step):
- delta_r = math.atan2(self.WHEEL_BASE, 1. / curvatures[i])
-
- A12 = (V / self.WHEEL_BASE) / (math.cos(delta_r)**2)
- A22 = (1. - 1. / self.tau * self.dt)
-
- Ad = np.array([[1., V * self.dt, 0.],
- [0., 1., A12 * self.dt],
- [0., 0., A22]])
-
- Bd = np.array([[0.], [0.], [1. / self.tau]]) * self.dt
-
- # -v*curvature + v/L*(tan(delta_r)-delta_r*cos_delta_r_squared_inv);
- # W_D_0 = V / self.WHEEL_BASE * (delta_r / (math.cos(delta_r)**2)
- W_D_0 = -V * curvatures[i] + (V / self.WHEEL_BASE) * (math.tan(delta_r) - delta_r / (math.cos(delta_r)**2))
-
- W_D = np.array([[0.], [W_D_0], [0.]]) * self.dt
-
- self.Ad_s.append(Ad)
- self.Bd_s.append(Bd)
- self.W_D_s.append(W_D)
-
- # return self.Ad_s, self.Bd_s, self.W_D_s
-
-def search_nearest_point(points, base_point):
- """
- Parameters
- -----------
- points : numpy.ndarray, shape is (2, N)
- base_point : numpy.ndarray, shape is (2, 1)
-
- Returns
- -------
- nearest_index :
- nearest_point :
- """
- distance_mat = np.sqrt(np.sum((points - base_point)**2, axis=0))
-
- index_min = np.argmin(distance_mat)
-
- return index_min, points[:, index_min]
-
-
-def main():
- # parameters
- dt = 0.01
- simulation_time = 20 # in seconds
- PREDICT_STEP = 30
- iteration_num = int(simulation_time / dt)
-
- # make simulator with coninuous matrix
- init_xs_lead = np.array([0., 0., math.pi/5, 0.])
- lead_car = WheeledSystem(init_states=init_xs_lead)
-
- # make system model
- lead_car_system_model = SystemModel()
-
- # reference
- history_traj_ref = []
- history_angle_ref = []
- traj_ref_xs, traj_ref_ys = make_sample_traj(int(simulation_time/dt))
- traj_ref = np.array([traj_ref_xs, traj_ref_ys])
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # get traj's curvature
- NUM_SKIP = 3
- MARGIN = 50
- angles, curvatures = calc_curvatures(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save traj ref
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # print(history_traj_ref)
- # input()
-
- # evaluation function weight
- Q = np.diag([1e2, 1., 1e3])
- R = np.diag([1e2])
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # make controller with discreted matrix
- lead_controller = IterativeMpcController(lead_car_system_model, Q, R, PREDICT_STEP,
- dt_input_upper=np.array([1 * dt]), dt_input_lower=np.array([-1 * dt]),
- input_upper=np.array([1.]), input_lower=np.array([-1.]))
-
-
- # initialize
- lead_controller.initialize_controller()
-
- for i in range(iteration_num):
- print("simulation time = {0}".format(i))
-
- ## lead
- # world traj
- lead_states = lead_car.xs
-
- # nearest point
- index_min, nearest_point = search_nearest_point(traj_ref, lead_car.xs[:2].reshape(2, 1))
-
- # end check
- if len(traj_ref_ys) <= index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN:
- print("break")
- break
-
- # get traj's curvature
- angles, curvatures = calc_curvatures(traj_ref[:, index_min+MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN], PREDICT_STEP, NUM_SKIP)
-
- # save
- history_traj_ref.append(traj_ref[:, index_min + MARGIN:index_min + PREDICT_STEP + 2 * NUM_SKIP + MARGIN])
- history_angle_ref.append(angles)
-
- # System model update
- V = calc_ideal_vel(traj_ref, dt) # in pratical we should calc from the state
- lead_car_system_model.calc_predict_sytem_model(V, curvatures, PREDICT_STEP)
-
- # transformation
- # car
- relative_car_position = coordinate_transformation_in_position(lead_states[:2].reshape(2, 1), nearest_point)
- relative_car_position = coordinate_transformation_in_angle(relative_car_position, angles[0])
-
- relative_car_angle = lead_states[2] - angles[0]
- relative_car_state = np.hstack((relative_car_position[1], relative_car_angle, lead_states[-1]))
-
- # traj_ref
- relative_traj = coordinate_transformation_in_position(traj_ref[:, index_min:index_min + PREDICT_STEP], nearest_point)
- relative_traj = coordinate_transformation_in_angle(relative_traj, angles[0])
- relative_ref_angle = np.array(angles) - angles[0]
-
- # make ref
- lead_reference = np.array([[relative_traj[1, -1], relative_ref_angle[-1], 0.] for i in range(PREDICT_STEP)]).flatten()
-
- print("relative car state = {}".format(relative_car_state))
- print("nearest point = {}".format(nearest_point))
- # input()
-
- # update system matrix
- lead_controller.update_system_model(lead_car_system_model)
-
- lead_opt_u, all_opt_u = lead_controller.calc_input(relative_car_state, lead_reference)
-
- lead_opt_u = np.hstack((np.array([V]), lead_opt_u))
-
- all_opt_u = np.stack((np.ones(PREDICT_STEP)*V, all_opt_u.flatten()))
-
- print("opt_u = {}".format(lead_opt_u))
- print("all_opt_u = {}".format(all_opt_u))
-
- # predict
- lead_car.predict_state(all_opt_u, dt=dt)
-
- # update
- lead_car.update_state(lead_opt_u, dt=dt)
-
- # print(lead_car.history_predict_xs)
- # input()
-
- # figures and animation
- lead_history_states = np.array(lead_car.history_xs)
- lead_history_predict_states = lead_car.history_predict_xs
-
- """
- time_history_fig = plt.figure()
- x_fig = time_history_fig.add_subplot(311)
- y_fig = time_history_fig.add_subplot(312)
- theta_fig = time_history_fig.add_subplot(313)
-
- car_traj_fig = plt.figure()
- traj_fig = car_traj_fig.add_subplot(111)
- traj_fig.set_aspect('equal')
-
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 0], label="lead")
- x_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 0], label="follow")
- x_fig.set_xlabel("time [s]")
- x_fig.set_ylabel("x")
- x_fig.legend()
-
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 1], label="lead")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 1], label="follow")
- y_fig.plot(np.arange(0, simulation_time+0.01, dt), [4. for _ in range(iteration_num+1)], linestyle="dashed")
- y_fig.set_xlabel("time [s]")
- y_fig.set_ylabel("y")
- y_fig.legend()
-
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_states[:, 2], label="lead")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_states[:, 2], label="follow")
- theta_fig.plot(np.arange(0, simulation_time+0.01, dt), [0. for _ in range(iteration_num+1)], linestyle="dashed")
- theta_fig.set_xlabel("time [s]")
- theta_fig.set_ylabel("theta")
- theta_fig.legend()
-
- time_history_fig.tight_layout()
-
- traj_fig.plot(lead_history_states[:, 0], lead_history_states[:, 1], label="lead")
- traj_fig.plot(follow_history_states[:, 0], follow_history_states[:, 1], label="follow")
- traj_fig.set_xlabel("x")
- traj_fig.set_ylabel("y")
- traj_fig.legend()
- plt.show()
-
- lead_history_us = np.array(lead_controller.history_us)
- follow_history_us = np.array(follow_controller.history_us)
- input_history_fig = plt.figure()
- u_1_fig = input_history_fig.add_subplot(111)
-
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), lead_history_us[:, 0], label="lead")
- u_1_fig.plot(np.arange(0, simulation_time+0.01, dt), follow_history_us[:, 0], label="follow")
- u_1_fig.set_xlabel("time [s]")
- u_1_fig.set_ylabel("u_omega")
-
- input_history_fig.tight_layout()
- plt.show()
- """
-
- animdrawer = AnimDrawer([lead_history_states, lead_history_predict_states, traj_ref, history_traj_ref, history_angle_ref])
- animdrawer.draw_anim()
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/mpc/extend/mpc_func_with_cvxopt.py b/mpc/extend/mpc_func_with_cvxopt.py
deleted file mode 100644
index a46d2d2..0000000
--- a/mpc/extend/mpc_func_with_cvxopt.py
+++ /dev/null
@@ -1,304 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-from cvxopt import matrix, solvers
-
-class MpcController():
- """
- Attributes
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- Qs : numpy.ndarray
- concatenated evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- Rs : numpy.ndarray
- concatenated evaluation function weight for inputs
- pre_step : int
- prediction step
- state_size : int
- state size of the plant
- input_size : int
- input size of the plant
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- """
- def __init__(self, A, B, W_D, Q, R, pre_step, initial_input=None, dt_input_upper=None, dt_input_lower=None, input_upper=None, input_lower=None):
- """
- Parameters
- ------------
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- Q : numpy.ndarray
- evaluation function weight for states
- R : numpy.ndarray
- evaluation function weight for inputs
- pre_step : int
- prediction step
- dt_input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- dt_input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input dt, default is None
- input_upper : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- input_lower : numpy.ndarray, shape(input_size, ), optional
- constraints of input, default is None
- history_us : list
- time history of optimal input us(numpy.ndarray)
- """
- self.A = np.array(A)
- self.B = np.array(B)
- self.W_D = np.array(W_D)
- self.Q = np.array(Q)
- self.R = np.array(R)
- self.pre_step = pre_step
-
- self.Qs = None
- self.Rs = None
-
- self.state_size = self.A.shape[0]
- self.input_size = self.B.shape[1]
-
- self.history_us = [np.zeros(self.input_size)]
-
- # initial state
- if initial_input is not None:
- self.history_us = [initial_input]
-
- # constraints
- self.dt_input_lower = dt_input_lower
- self.dt_input_upper = dt_input_upper
- self.input_upper = input_upper
- self.input_lower = input_lower
-
- # about mpc matrix
- self.W = None
- self.omega = None
- self.F = None
- self.f = None
-
- def initialize_controller(self):
- """
- make matrix to calculate optimal control input
-
- """
- A_factorials = [self.A]
-
- self.phi_mat = copy.deepcopy(self.A)
-
- for _ in range(self.pre_step - 1):
- temp_mat = np.dot(A_factorials[-1], self.A)
- self.phi_mat = np.vstack((self.phi_mat, temp_mat))
-
- A_factorials.append(temp_mat) # after we use this factorials
-
- print("phi_mat = \n{0}".format(self.phi_mat))
-
- self.gamma_mat = copy.deepcopy(self.B)
- gammma_mat_temp = copy.deepcopy(self.B)
-
- for i in range(self.pre_step - 1):
- temp_1_mat = np.dot(A_factorials[i], self.B)
- gammma_mat_temp = temp_1_mat + gammma_mat_temp
- self.gamma_mat = np.vstack((self.gamma_mat, gammma_mat_temp))
-
- print("gamma_mat = \n{0}".format(self.gamma_mat))
-
- self.theta_mat = copy.deepcopy(self.gamma_mat)
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(self.gamma_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = self.gamma_mat[:-int((i + 1)*self.state_size) , :]
-
- self.theta_mat = np.hstack((self.theta_mat, temp_mat))
-
- print("theta_mat = \n{0}".format(self.theta_mat))
-
- # disturbance
- print("A_factorials_mat = \n{0}".format(A_factorials))
- A_factorials_mat = np.array(A_factorials).reshape(-1, self.state_size)
- print("A_factorials_mat = \n{0}".format(A_factorials_mat))
-
- eye = np.eye(self.state_size)
- self.dist_mat = np.vstack((eye, A_factorials_mat[:-self.state_size, :]))
- base_mat = copy.deepcopy(self.dist_mat)
-
- print("base_mat = \n{0}".format(base_mat))
-
- for i in range(self.pre_step - 1):
- temp_mat = np.zeros_like(A_factorials_mat)
- temp_mat[int((i + 1)*self.state_size): , :] = base_mat[:-int((i + 1)*self.state_size) , :]
- self.dist_mat = np.hstack((self.dist_mat, temp_mat))
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- W_Ds = copy.deepcopy(self.W_D)
-
- for _ in range(self.pre_step - 1):
- W_Ds = np.vstack((W_Ds, self.W_D))
-
- self.dist_mat = np.dot(self.dist_mat, W_Ds)
-
- print("dist_mat = \n{0}".format(self.dist_mat))
-
- # evaluation function weight
- diag_Qs = np.array([np.diag(self.Q) for _ in range(self.pre_step)])
- diag_Rs = np.array([np.diag(self.R) for _ in range(self.pre_step)])
-
- self.Qs = np.diag(diag_Qs.flatten())
- self.Rs = np.diag(diag_Rs.flatten())
-
- print("Qs = \n{0}".format(self.Qs))
- print("Rs = \n{0}".format(self.Rs))
-
- # constraints
- # about dt U
- if self.input_lower is not None:
- # initialize
- self.F = np.zeros((self.input_size * 2, self.pre_step * self.input_size))
- for i in range(self.input_size):
- self.F[i * 2: (i + 1) * 2, i] = np.array([1., -1.])
- temp_F = copy.deepcopy(self.F)
-
- print("F = \n{0}".format(self.F))
-
- for i in range(self.pre_step - 1):
- temp_F = copy.deepcopy(temp_F)
-
- for j in range(self.input_size):
- temp_F[j * 2: (j + 1) * 2, ((i+1) * self.input_size) + j] = np.array([1., -1.])
-
- self.F = np.vstack((self.F, temp_F))
-
- self.F1 = self.F[:, :self.input_size]
-
- temp_f = []
-
- for i in range(self.input_size):
- temp_f.append(-1 * self.input_upper[i])
- temp_f.append(self.input_lower[i])
-
- self.f = np.array([temp_f for _ in range(self.pre_step)]).flatten()
-
- print("F = \n{0}".format(self.F))
- print("F1 = \n{0}".format(self.F1))
- print("f = \n{0}".format(self.f))
-
- # about dt_u
- if self.dt_input_lower is not None:
- self.W = np.zeros((2, self.pre_step * self.input_size))
- self.W[:, 0] = np.array([1., -1.])
-
- for i in range(self.pre_step * self.input_size - 1):
- temp_W = np.zeros((2, self.pre_step * self.input_size))
- temp_W[:, i+1] = np.array([1., -1.])
- self.W = np.vstack((self.W, temp_W))
-
- temp_omega = []
-
- for i in range(self.input_size):
- temp_omega.append(self.dt_input_upper[i])
- temp_omega.append(-1. * self.dt_input_lower[i])
-
- self.omega = np.array([temp_omega for _ in range(self.pre_step)]).flatten()
-
- print("W = \n{0}".format(self.W))
- print("omega = \n{0}".format(self.omega))
-
- # about state
- print("check the matrix!! if you think rite, plese push enter")
- # input()
-
- def calc_input(self, states, references):
- """calculate optimal input
- Parameters
- -----------
- states : numpy.ndarray, shape(state length, )
- current state of system
- references : numpy.ndarray, shape(state length * pre_step, )
- reference of the system, you should set this value as reachable goal
-
- References
- ------------
- opt_input : numpy.ndarray, shape(input_length, )
- optimal input
- """
- temp_1 = np.dot(self.phi_mat, states.reshape(-1, 1))
- temp_2 = np.dot(self.gamma_mat, self.history_us[-1].reshape(-1, 1))
-
- error = references.reshape(-1, 1) - temp_1 - temp_2 - self.dist_mat
-
- G = 2. * np.dot(self.theta_mat.T, np.dot(self.Qs, error))
-
- H = np.dot(self.theta_mat.T, np.dot(self.Qs, self.theta_mat)) + self.Rs
-
- # constraints
- A = []
- b = []
-
- if self.W is not None:
- A.append(self.W)
- b.append(self.omega.reshape(-1, 1))
-
- if self.F is not None:
- b_F = - np.dot(self.F1, self.history_us[-1].reshape(-1, 1)) - self.f.reshape(-1, 1)
- A.append(self.F)
- b.append(b_F)
-
- A = np.array(A).reshape(-1, self.input_size * self.pre_step)
-
- ub = np.array(b).flatten()
-
- # make cvxpy problem formulation
- P = 2*matrix(H)
- q = matrix(-1 * G)
- A = matrix(A)
- b = matrix(ub)
-
- # constraint
- if self.W is not None or self.F is not None :
- opt_result = solvers.qp(P, q, G=A, h=b)
-
- opt_dt_us = list(opt_result['x'])
-
- opt_u = opt_dt_us[:self.input_size] + self.history_us[-1]
-
- # save
- self.history_us.append(opt_u)
-
- return opt_u
-
- def update_system_model(self, A, B, W_D):
- """update system model
- A : numpy.ndarray
- system matrix
- B : numpy.ndarray
- input matrix
- W_D : numpy.ndarray
- distubance matrix in state equation
- """
-
- self.A = A
- self.B = B
- self.W_D = W_D
-
- self.initialize_controller()
diff --git a/mpc/extend/traj_func.py b/mpc/extend/traj_func.py
deleted file mode 100644
index 8f5ce18..0000000
--- a/mpc/extend/traj_func.py
+++ /dev/null
@@ -1,31 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-
-def make_sample_traj(NUM, dt=0.01, a=30.):
- """
- make sample trajectory
- Parameters
- ------------
- NUM : int
- dt : float
- a : float
-
- Returns
- ----------
- traj_xs : list
- traj_ys : list
- """
- DELAY = 2.
- traj_xs = []
- traj_ys = []
-
- for i in range(NUM):
- traj_xs.append(i * 0.1)
- traj_ys.append(a * math.sin(dt * i / DELAY))
-
- plt.plot(traj_xs, traj_ys)
- plt.show()
-
- return traj_xs, traj_ys
-
diff --git a/nmpc/cgmres/README.md b/nmpc/cgmres/README.md
deleted file mode 100644
index a46901c..0000000
--- a/nmpc/cgmres/README.md
+++ /dev/null
@@ -1,79 +0,0 @@
-# CGMRES method of Nonlinear Model Predictive Control
-This program is about Continuous gmres method for NMPC
-Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
-By using CGMRES, we can pass the calculating step and get the optimal input quickly.
-
-# Problem Formulation
-
-- **example**
-
-- model
-
- -
-you can confirm that the my method could consider the constraints of input.
-
-- two wheeled model
-
-coming soon !
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-coming soon !
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
diff --git a/nmpc/newton/main_example.py b/nmpc/newton/main_example.py
deleted file mode 100644
index 4ab4a4c..0000000
--- a/nmpc/newton/main_example.py
+++ /dev/null
@@ -1,657 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(copy.deepcopy(self.x_1))
- self.history_x_2.append(copy.deepcopy(self.x_2))
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = np.zeros(N+1)
- x_2s = np.zeros(N+1)
-
- # input initial state
- x_1s[0] = x_1
- x_2s[0] = x_2
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s[i+1] = temp_x_1
- x_2s[i+1] = temp_x_2
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = np.zeros(N)
- lam_2s = np.zeros(N)
-
- # input final state
- lam_1s[-1] = x_1s[-1]
- lam_2s[-1] = x_2s[-1]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[i] ,lam_2s[i], us[i], dt)
- lam_1s[i-1] = temp_lam_1
- lam_2s[i-1] = temp_lam_2
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-
-def calc_numerical_gradient(forward_prop, grad_f, all_us, shape, input_size):
- """
- Parameters
- ------------
- forward_prop : function
- forward prop
- grad_f : function
- gradient function
- all_us : numpy.ndarray, shape(pred_len, input_size*3)
- all inputs including with dummy input
- shape : tuple
- shape of Jacobian
- input_size : int
- input size of system
-
- Returns
- ---------
- grad : numpy.ndarray, shape is the same as shape
- results of numercial gradient of the input
-
- References
- -----------
- - oreilly japan 0 から作るdeeplearning
- https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/gradient.py
- """
- h = 1e-3 # 0.01
- grad = np.zeros(shape)
- grad_idx = 0
-
- it = np.nditer(all_us, flags=['multi_index'], op_flags=['readwrite'])
- while not it.finished:
- # get index
- idx = it.multi_index
- # save and return
- tmp_val = all_us[idx]
-
- # 差分を取る
- # 上側の差分
- all_us[idx] = float(tmp_val) + h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh1 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- # 下側の差分
- all_us[idx] = float(tmp_val) - h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh2 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- grad[:, grad_idx] = ((fuh1 - fuh2) / (2.*h)).flatten() # to flat でgradに代入できるように
-
- all_us[idx] = tmp_val
- it.iternext()
- grad_idx += 1
-
- return np.array(grad)
-
-class NMPCControllerWithNewton():
- """
- Attributes
- ------------
- N : int
- predicte step, discritize value
- threshold : float
- newton's threshold value
- NUM_INPUT : int
- system input length, this should include dummy u and constraint variables
- MAX_ITERATION : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.N = 10 # time step
- self.threshold = 0.0001 # break
-
- self.NUM_ALL_INPUT = 3 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.NUM_INPUT = 1 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.Jacobian_size = self.NUM_ALL_INPUT * self.N
-
- # newton parameters
- self.MAX_ITERATION = 100
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros((self.N, self.NUM_INPUT))
- self.dummy_us = np.ones((self.N, self.NUM_INPUT)) * 0.25
- self.raws = np.ones((self.N, self.NUM_INPUT)) * 0.01
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = 0.01
-
- # concat all us, shape (pred_len, input_size)
- all_us = np.hstack((self.us, self.dummy_us, self.raws))
-
- # Newton method
- for i in range(self.MAX_ITERATION):
- # calc all state
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- # F
- F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # judge
- if np.linalg.norm(F_hat) < self.threshold:
- # print("break!!")
- break
-
- grad_f = lambda x_1s, x_2s, lam_1s, lam_2s, all_us : self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
- forward_prop_f = lambda us : self.simulator.calc_predict_and_adjoint_state(x_1, x_2, us, self.N, dt)
- grads = calc_numerical_gradient(forward_prop_f, grad_f, all_us, (self.Jacobian_size, self.Jacobian_size), self.NUM_INPUT)
-
- # make jacobian and calc inverse of it
- # grads += np.eye(self.Jacobian_size) * 1e-8
- try:
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
- except np.linalg.LinAlgError:
- print("Warning : singular matrix!!")
- grads += np.eye(self.Jacobian_size) * 1e-10 # add noise
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
-
- all_us = all_us.reshape(self.N, self.NUM_ALL_INPUT)
-
- # update
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- # final insert
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, all_us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = np.zeros((N, self.NUM_INPUT*3))
-
- us = all_us[:, :self.NUM_INPUT].flatten()
- dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT].flatten()
- raws = all_us[:, 2*self.NUM_INPUT:].flatten()
-
- for i in range(N):
- F_u = 0.5 * us[i] + lam_2s[i] + 2. * raws[i] * us[i]
- F_dummy = -0.01 + 2. * raws[i] * dummy_us[i]
- F_raw = us[i]**2 + dummy_us[i]**2 - 0.5**2
-
- F[i] = np.array([F_u, F_dummy, F_raw])
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCControllerWithNewton()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- print("iteration = {}".format(i))
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/scripts/simple_run.py b/scripts/simple_run.py
new file mode 100644
index 0000000..510e24e
--- /dev/null
+++ b/scripts/simple_run.py
@@ -0,0 +1,53 @@
+import argparse
+
+from PythonLinearNonlinearControl.helper import bool_flag, make_logger
+from PythonLinearNonlinearControl.controllers.make_controllers import make_controller
+from PythonLinearNonlinearControl.planners.make_planners import make_planner
+from PythonLinearNonlinearControl.configs.make_configs import make_config
+from PythonLinearNonlinearControl.models.make_models import make_model
+from PythonLinearNonlinearControl.envs.make_envs import make_env
+from PythonLinearNonlinearControl.runners.make_runners import make_runner
+from PythonLinearNonlinearControl.plotters.plot_func import plot_results
+
+def run(args):
+ # logger
+ make_logger(args.result_dir)
+
+ # make envs
+ env = make_env(args)
+
+ # make config
+ config = make_config(args)
+
+ # make planner
+ planner = make_planner(args, config)
+
+ # make model
+ model = make_model(args, config)
+
+ # make controller
+ controller = make_controller(args, config, model)
+
+ # make simulator
+ runner = make_runner(args)
+
+ # run experiment
+ history_x, history_u, history_g = runner.run(env, controller, planner)
+
+ # plot results
+ plot_results(args, history_x, history_u, history_g=history_g)
+
+def main():
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--controller_type", type=str, default="MPC")
+ parser.add_argument("--planner_type", type=str, default="const")
+ parser.add_argument("--env", type=str, default="FirstOrderLag")
+ parser.add_argument("--result_dir", type=str, default="./result")
+
+ args = parser.parse_args()
+
+ run(args)
+
+if __name__ == "__main__":
+ main()
\ No newline at end of file
diff --git a/setup.py b/setup.py
new file mode 100644
index 0000000..7ea6a7c
--- /dev/null
+++ b/setup.py
@@ -0,0 +1,21 @@
+from setuptools import find_packages
+from setuptools import setup
+
+install_requires = ['numpy', 'matplotlib', 'cvxopt']
+tests_require = ['pytest']
+setup_requires = ["pytest-runner"]
+
+setup(
+ name='PythonLinearNonlinearControl',
+ version='2.0',
+ description='Implementing linear and non-linear control method in python',
+ author='Shunichi Sekiguchi',
+ author_email='quick1st97of@gmail.com',
+ install_requires=install_requires,
+ url='https://github.com/Shunichi09/PythonLinearNonlinearControl',
+ license='MIT License',
+ packages=find_packages(exclude=('tests')),
+ setup_requires=setup_requires,
+ test_suite='tests',
+ tests_require=tests_require
+)
\ No newline at end of file
diff --git a/tests/__init__.py b/tests/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/__init__.py b/tests/configs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/test_first_order_lag.py b/tests/configs/test_first_order_lag.py
new file mode 100644
index 0000000..a013fac
--- /dev/null
+++ b/tests/configs/test_first_order_lag.py
@@ -0,0 +1,34 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.configs.first_order_lag \
+ import FirstOrderLagConfigModule
+
+class TestCalcCost():
+ def test_calc_costs(self):
+ # make config
+ config = FirstOrderLagConfigModule()
+ # set
+ pred_len = 5
+ state_size = 4
+ input_size = 2
+ pop_size = 2
+ pred_xs = np.ones((pop_size, pred_len, state_size))
+ g_xs = np.ones((pop_size, pred_len, state_size)) * 0.5
+ input_samples = np.ones((pop_size, pred_len, input_size)) * 0.5
+
+ costs = config.input_cost_fn(input_samples)
+ expected_costs = np.ones((pop_size, pred_len, input_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.R))
+
+ costs = config.state_cost_fn(pred_xs, g_xs)
+ expected_costs = np.ones((pop_size, pred_len, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Q))
+
+ costs = config.terminal_state_cost_fn(pred_xs[:, -1, :],\
+ g_xs[:, -1, :])
+ expected_costs = np.ones((pop_size, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Sf))
\ No newline at end of file
diff --git a/tests/models/__init__.py b/tests/models/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/models/test_model.py b/tests/models/test_model.py
new file mode 100644
index 0000000..e11a439
--- /dev/null
+++ b/tests/models/test_model.py
@@ -0,0 +1,53 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.models.model import LinearModel
+
+class TestLinearModel():
+ """
+ """
+ def test_predict(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ assert pred_xs == pytest.approx(np.array([[0.5, 0.5], [0.75, 1.3]]))
+
+ def test_alltogether(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ u = np.tile(u, (1, 1, 1))
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)[0]
+
+ assert pred_xs_alltogether == pytest.approx(pred_xs)
+
+ def test_alltogether_val(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.stack((np.ones((1, 1)), np.ones((1, 1))*0.5), axis=0)
+
+ linear_model = LinearModel(A, B)
+
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)
+
+ expected_val = np.array([[[0.5, 0.5], [0.75, 1.3]],
+ [[0.5, 0.5], [0.65, 1.05]]])
+
+ assert pred_xs_alltogether == pytest.approx(expected_val)
\ No newline at end of file
-
-you can confirm that the my method could consider the constraints of input.
-
-- two wheeled model
-
-coming soon !
-
-# Usage
-
-- for example
-
-```
-$ python main_example.py
-```
-
-- for two wheeled
-
-coming soon !
-
-# Requirement
-
-- python3.5 or more
-- numpy
-- matplotlib
-
-# Reference
-I`m sorry that main references are written in Japanese
-
-- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
-
-- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
-
-- 非線形最適制御入門(コロナ社)
-
-- 実時間最適化による制御の実応用(コロナ社)
diff --git a/nmpc/newton/main_example.py b/nmpc/newton/main_example.py
deleted file mode 100644
index 4ab4a4c..0000000
--- a/nmpc/newton/main_example.py
+++ /dev/null
@@ -1,657 +0,0 @@
-import numpy as np
-import matplotlib.pyplot as plt
-import math
-import copy
-
-class SampleSystem():
- """SampleSystem, this is the simulator
- Attributes
- -----------
- x_1 : float
- system state 1
- x_2 : float
- system state 2
- history_x_1 : list
- time history of system state 1 (x_1)
- history_x_2 : list
- time history of system state 2 (x_2)
- """
- def __init__(self, init_x_1=0., init_x_2=0.):
- """
- Palameters
- -----------
- init_x_1 : float, optional
- initial value of x_1, default is 0.
- init_x_2 : float, optional
- initial value of x_2, default is 0.
- """
- self.x_1 = init_x_1
- self.x_2 = init_x_2
- self.history_x_1 = [init_x_1]
- self.history_x_2 = [init_x_2]
-
- def update_state(self, u, dt=0.01):
- """
- Palameters
- ------------
- u : float
- input of system in some cases this means the reference
- dt : float in seconds, optional
- sampling time of simulation, default is 0.01 [s]
- """
- # for theta 1, theta 1 dot, theta 2, theta 2 dot
- k0 = [0.0 for _ in range(2)]
- k1 = [0.0 for _ in range(2)]
- k2 = [0.0 for _ in range(2)]
- k3 = [0.0 for _ in range(2)]
-
- functions = [self._func_x_1, self._func_x_2]
-
- # solve Runge-Kutta
- for i, func in enumerate(functions):
- k0[i] = dt * func(self.x_1, self.x_2, u)
-
- for i, func in enumerate(functions):
- k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
-
- for i, func in enumerate(functions):
- k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
-
- for i, func in enumerate(functions):
- k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
-
- self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
- self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
-
- # save
- self.history_x_1.append(copy.deepcopy(self.x_1))
- self.history_x_2.append(copy.deepcopy(self.x_2))
-
- def _func_x_1(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = y_2
- return y_dot
-
- def _func_x_2(self, y_1, y_2, u):
- """
- Parameters
- ------------
- y_1 : float
- y_2 : float
- u : float
- system input
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
-
-class NMPCSimulatorSystem():
- """SimulatorSystem for nmpc, this is the simulator of nmpc
- the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
- Attributes
- -----------
-
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- pass
-
- def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
- """main
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
-
- x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
- lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
-
- return x_1s, x_2s, lam_1s, lam_2s
-
- def _calc_predict_states(self, x_1, x_2, us, N, dt):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- """
- # initial state
- x_1s = np.zeros(N+1)
- x_2s = np.zeros(N+1)
-
- # input initial state
- x_1s[0] = x_1
- x_2s[0] = x_2
-
- for i in range(N):
- temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
- x_1s[i+1] = temp_x_1
- x_2s[i+1] = temp_x_2
-
- return x_1s, x_2s
-
- def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- us : list of float
- estimated optimal input Us for N steps
- N : int
- predict step
- dt : float
- sampling time
-
- Returns
- --------
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- """
- # final state
- # final_state_func
- lam_1s = np.zeros(N)
- lam_2s = np.zeros(N)
-
- # input final state
- lam_1s[-1] = x_1s[-1]
- lam_2s[-1] = x_2s[-1]
-
- for i in range(N-1, 0, -1):
- temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[i] ,lam_2s[i], us[i], dt)
- lam_1s[i-1] = temp_lam_1
- lam_2s[i-1] = temp_lam_2
-
- return lam_1s, lam_2s
-
- def final_state_func(self):
- """this func usually need
- """
- pass
-
- def _predict_state_with_oylar(self, x_1, x_2, u, dt):
- """in this case this function is the same as simulator
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- next_x_1 : float
- next state, x_1 calculated by using state equation
- next_x_2 : float
- next state, x_2 calculated by using state equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self.func_x_1, self.func_x_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, u)
-
- next_x_1 = x_1 + k0[0]
- next_x_2 = x_2 + k0[1]
-
- return next_x_1, next_x_2
-
- def func_x_1(self, y_1, y_2, u):
- """calculating \dot{x_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_1}
- """
- y_dot = y_2
- return y_dot
-
- def func_x_2(self, y_1, y_2, u):
- """calculating \dot{x_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means \dot{x_2}
- """
- y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
- return y_dot
-
- def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
- """
- Parameters
- ------------
- x_1 : float
- system state
- x_2 : float
- system state
- lam_1 : float
- adjoint state
- lam_2 : float
- adjoint state
- u : float
- system input
- dt : float in seconds
- sampling time
- Returns
- --------
- pre_lam_1 : float
- pre, 1 step before lam_1 calculated by using adjoint equation
- pre_lam_2 : float
- pre, 1 step before lam_2 calculated by using adjoint equation
- """
- k0 = [0. for _ in range(2)]
-
- functions = [self._func_lam_1, self._func_lam_2]
-
- for i, func in enumerate(functions):
- k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
-
- pre_lam_1 = lam_1 + k0[0]
- pre_lam_2 = lam_2 + k0[1]
-
- return pre_lam_1, pre_lam_2
-
- def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_1}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_1}
- """
- y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
- return y_dot
-
- def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
- """calculating -\dot{lam_2}
- Parameters
- ------------
- y_1 : float
- means x_1
- y_2 : float
- means x_2
- y_3 : float
- means lam_1
- y_4 : float
- means lam_2
- u : float
- means system input
- Returns
- ---------
- y_dot : float
- means -\dot{lam_2}
- """
- y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
- return y_dot
-
-
-def calc_numerical_gradient(forward_prop, grad_f, all_us, shape, input_size):
- """
- Parameters
- ------------
- forward_prop : function
- forward prop
- grad_f : function
- gradient function
- all_us : numpy.ndarray, shape(pred_len, input_size*3)
- all inputs including with dummy input
- shape : tuple
- shape of Jacobian
- input_size : int
- input size of system
-
- Returns
- ---------
- grad : numpy.ndarray, shape is the same as shape
- results of numercial gradient of the input
-
- References
- -----------
- - oreilly japan 0 から作るdeeplearning
- https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/gradient.py
- """
- h = 1e-3 # 0.01
- grad = np.zeros(shape)
- grad_idx = 0
-
- it = np.nditer(all_us, flags=['multi_index'], op_flags=['readwrite'])
- while not it.finished:
- # get index
- idx = it.multi_index
- # save and return
- tmp_val = all_us[idx]
-
- # 差分を取る
- # 上側の差分
- all_us[idx] = float(tmp_val) + h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh1 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- # 下側の差分
- all_us[idx] = float(tmp_val) - h
- us = all_us[:, :input_size]
- x_1s, x_2s, lam_1s, lam_2s = forward_prop(us) # forward
- fuh2 = grad_f(x_1s, x_2s, lam_1s, lam_2s, all_us)
-
- grad[:, grad_idx] = ((fuh1 - fuh2) / (2.*h)).flatten() # to flat でgradに代入できるように
-
- all_us[idx] = tmp_val
- it.iternext()
- grad_idx += 1
-
- return np.array(grad)
-
-class NMPCControllerWithNewton():
- """
- Attributes
- ------------
- N : int
- predicte step, discritize value
- threshold : float
- newton's threshold value
- NUM_INPUT : int
- system input length, this should include dummy u and constraint variables
- MAX_ITERATION : int
- decide by the solved matrix size
- simulator : NMPCSimulatorSystem class
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- history_u : list of float
- time history of actual system input
- history_dummy_u : list of float
- time history of actual dummy u
- history_raw : list of float
- time history of actual raw
- history_f : list of float
- time history of error of optimal
- """
- def __init__(self):
- """
- Parameters
- -----------
- None
- """
- # parameters
- self.N = 10 # time step
- self.threshold = 0.0001 # break
-
- self.NUM_ALL_INPUT = 3 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.NUM_INPUT = 1 # u with dummy, and 制約条件に対するrawにも合わせた入力の数
- self.Jacobian_size = self.NUM_ALL_INPUT * self.N
-
- # newton parameters
- self.MAX_ITERATION = 100
-
- # simulator
- self.simulator = NMPCSimulatorSystem()
-
- # initial
- self.us = np.zeros((self.N, self.NUM_INPUT))
- self.dummy_us = np.ones((self.N, self.NUM_INPUT)) * 0.25
- self.raws = np.ones((self.N, self.NUM_INPUT)) * 0.01
-
- # for fig
- self.history_u = []
- self.history_dummy_u = []
- self.history_raw = []
- self.history_f = []
-
- def calc_input(self, x_1, x_2, time):
- """
- Parameters
- ------------
- x_1 : float
- current state
- x_2 : float
- current state
- time : float in seconds
- now time
- Returns
- --------
- us : list of float
- estimated optimal system input
- """
- # calculating sampling time
- dt = 0.01
-
- # concat all us, shape (pred_len, input_size)
- all_us = np.hstack((self.us, self.dummy_us, self.raws))
-
- # Newton method
- for i in range(self.MAX_ITERATION):
- # calc all state
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- # F
- F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # judge
- if np.linalg.norm(F_hat) < self.threshold:
- # print("break!!")
- break
-
- grad_f = lambda x_1s, x_2s, lam_1s, lam_2s, all_us : self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
- forward_prop_f = lambda us : self.simulator.calc_predict_and_adjoint_state(x_1, x_2, us, self.N, dt)
- grads = calc_numerical_gradient(forward_prop_f, grad_f, all_us, (self.Jacobian_size, self.Jacobian_size), self.NUM_INPUT)
-
- # make jacobian and calc inverse of it
- # grads += np.eye(self.Jacobian_size) * 1e-8
- try:
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
- except np.linalg.LinAlgError:
- print("Warning : singular matrix!!")
- grads += np.eye(self.Jacobian_size) * 1e-10 # add noise
- all_us = all_us.reshape(-1, 1) - np.dot(np.linalg.inv(grads), F_hat.reshape(-1, 1))
-
- all_us = all_us.reshape(self.N, self.NUM_ALL_INPUT)
-
- # update
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- # final insert
- self.us = all_us[:, :self.NUM_INPUT]
- self.dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT]
- self.raws = all_us[:, 2*self.NUM_INPUT:]
-
- x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
-
- F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
-
- # for save
- self.history_f.append(np.linalg.norm(F))
- self.history_u.append(self.us[0])
- self.history_dummy_u.append(self.dummy_us[0])
- self.history_raw.append(self.raws[0])
-
- return self.us
-
- def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, all_us, N, dt):
- """
- Parameters
- ------------
- x_1s : list of float
- predicted x_1s for N steps
- x_2s : list of float
- predicted x_2s for N steps
- lam_1s : list of float
- adjoint state of x_1s, lam_1s for N steps
- lam_2s : list of float
- adjoint state of x_2s, lam_2s for N steps
- us : list of float
- estimated optimal system input
- dummy_us : list of float
- estimated dummy input
- raws : list of float
- estimated constraint variable
- N : int
- predict time step
- dt : float
- sampling time of system
- """
- F = np.zeros((N, self.NUM_INPUT*3))
-
- us = all_us[:, :self.NUM_INPUT].flatten()
- dummy_us = all_us[:, self.NUM_INPUT:2*self.NUM_INPUT].flatten()
- raws = all_us[:, 2*self.NUM_INPUT:].flatten()
-
- for i in range(N):
- F_u = 0.5 * us[i] + lam_2s[i] + 2. * raws[i] * us[i]
- F_dummy = -0.01 + 2. * raws[i] * dummy_us[i]
- F_raw = us[i]**2 + dummy_us[i]**2 - 0.5**2
-
- F[i] = np.array([F_u, F_dummy, F_raw])
-
- return np.array(F)
-
-def main():
- # simulation time
- dt = 0.01
- iteration_time = 20.
- iteration_num = int(iteration_time/dt)
-
- # plant
- plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
-
- # controller
- controller = NMPCControllerWithNewton()
-
- # for i in range(iteration_num)
- for i in range(1, iteration_num):
- print("iteration = {}".format(i))
- time = float(i) * dt
- x_1 = plant_system.x_1
- x_2 = plant_system.x_2
- # make input
- us = controller.calc_input(x_1, x_2, time)
- # update state
- plant_system.update_state(us[0])
-
- # figure
- fig = plt.figure()
-
- x_1_fig = fig.add_subplot(321)
- x_2_fig = fig.add_subplot(322)
- u_fig = fig.add_subplot(323)
- dummy_fig = fig.add_subplot(324)
- raw_fig = fig.add_subplot(325)
- f_fig = fig.add_subplot(326)
-
- x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
- x_1_fig.set_xlabel("time [s]")
- x_1_fig.set_ylabel("x_1")
-
- x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
- x_2_fig.set_xlabel("time [s]")
- x_2_fig.set_ylabel("x_2")
-
- u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
- u_fig.set_xlabel("time [s]")
- u_fig.set_ylabel("u")
-
- dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
- dummy_fig.set_xlabel("time [s]")
- dummy_fig.set_ylabel("dummy u")
-
- raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
- raw_fig.set_xlabel("time [s]")
- raw_fig.set_ylabel("raw")
-
- f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
- f_fig.set_xlabel("time [s]")
- f_fig.set_ylabel("optimal error")
-
- fig.tight_layout()
-
- plt.show()
-
-
-if __name__ == "__main__":
- main()
\ No newline at end of file
diff --git a/scripts/simple_run.py b/scripts/simple_run.py
new file mode 100644
index 0000000..510e24e
--- /dev/null
+++ b/scripts/simple_run.py
@@ -0,0 +1,53 @@
+import argparse
+
+from PythonLinearNonlinearControl.helper import bool_flag, make_logger
+from PythonLinearNonlinearControl.controllers.make_controllers import make_controller
+from PythonLinearNonlinearControl.planners.make_planners import make_planner
+from PythonLinearNonlinearControl.configs.make_configs import make_config
+from PythonLinearNonlinearControl.models.make_models import make_model
+from PythonLinearNonlinearControl.envs.make_envs import make_env
+from PythonLinearNonlinearControl.runners.make_runners import make_runner
+from PythonLinearNonlinearControl.plotters.plot_func import plot_results
+
+def run(args):
+ # logger
+ make_logger(args.result_dir)
+
+ # make envs
+ env = make_env(args)
+
+ # make config
+ config = make_config(args)
+
+ # make planner
+ planner = make_planner(args, config)
+
+ # make model
+ model = make_model(args, config)
+
+ # make controller
+ controller = make_controller(args, config, model)
+
+ # make simulator
+ runner = make_runner(args)
+
+ # run experiment
+ history_x, history_u, history_g = runner.run(env, controller, planner)
+
+ # plot results
+ plot_results(args, history_x, history_u, history_g=history_g)
+
+def main():
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--controller_type", type=str, default="MPC")
+ parser.add_argument("--planner_type", type=str, default="const")
+ parser.add_argument("--env", type=str, default="FirstOrderLag")
+ parser.add_argument("--result_dir", type=str, default="./result")
+
+ args = parser.parse_args()
+
+ run(args)
+
+if __name__ == "__main__":
+ main()
\ No newline at end of file
diff --git a/setup.py b/setup.py
new file mode 100644
index 0000000..7ea6a7c
--- /dev/null
+++ b/setup.py
@@ -0,0 +1,21 @@
+from setuptools import find_packages
+from setuptools import setup
+
+install_requires = ['numpy', 'matplotlib', 'cvxopt']
+tests_require = ['pytest']
+setup_requires = ["pytest-runner"]
+
+setup(
+ name='PythonLinearNonlinearControl',
+ version='2.0',
+ description='Implementing linear and non-linear control method in python',
+ author='Shunichi Sekiguchi',
+ author_email='quick1st97of@gmail.com',
+ install_requires=install_requires,
+ url='https://github.com/Shunichi09/PythonLinearNonlinearControl',
+ license='MIT License',
+ packages=find_packages(exclude=('tests')),
+ setup_requires=setup_requires,
+ test_suite='tests',
+ tests_require=tests_require
+)
\ No newline at end of file
diff --git a/tests/__init__.py b/tests/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/__init__.py b/tests/configs/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/configs/test_first_order_lag.py b/tests/configs/test_first_order_lag.py
new file mode 100644
index 0000000..a013fac
--- /dev/null
+++ b/tests/configs/test_first_order_lag.py
@@ -0,0 +1,34 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.configs.first_order_lag \
+ import FirstOrderLagConfigModule
+
+class TestCalcCost():
+ def test_calc_costs(self):
+ # make config
+ config = FirstOrderLagConfigModule()
+ # set
+ pred_len = 5
+ state_size = 4
+ input_size = 2
+ pop_size = 2
+ pred_xs = np.ones((pop_size, pred_len, state_size))
+ g_xs = np.ones((pop_size, pred_len, state_size)) * 0.5
+ input_samples = np.ones((pop_size, pred_len, input_size)) * 0.5
+
+ costs = config.input_cost_fn(input_samples)
+ expected_costs = np.ones((pop_size, pred_len, input_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.R))
+
+ costs = config.state_cost_fn(pred_xs, g_xs)
+ expected_costs = np.ones((pop_size, pred_len, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Q))
+
+ costs = config.terminal_state_cost_fn(pred_xs[:, -1, :],\
+ g_xs[:, -1, :])
+ expected_costs = np.ones((pop_size, state_size))*0.5
+
+ assert costs == pytest.approx(expected_costs**2 * np.diag(config.Sf))
\ No newline at end of file
diff --git a/tests/models/__init__.py b/tests/models/__init__.py
new file mode 100644
index 0000000..e69de29
diff --git a/tests/models/test_model.py b/tests/models/test_model.py
new file mode 100644
index 0000000..e11a439
--- /dev/null
+++ b/tests/models/test_model.py
@@ -0,0 +1,53 @@
+import pytest
+import numpy as np
+
+from PythonLinearNonlinearControl.models.model import LinearModel
+
+class TestLinearModel():
+ """
+ """
+ def test_predict(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ assert pred_xs == pytest.approx(np.array([[0.5, 0.5], [0.75, 1.3]]))
+
+ def test_alltogether(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.ones((1, 1))
+
+ linear_model = LinearModel(A, B)
+ pred_xs = linear_model.predict_traj(curr_x, u)
+
+ u = np.tile(u, (1, 1, 1))
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)[0]
+
+ assert pred_xs_alltogether == pytest.approx(pred_xs)
+
+ def test_alltogether_val(self):
+
+ A = np.array([[1., 0.1],
+ [0.1, 1.5]])
+ B = np.array([[0.2], [0.5]])
+ curr_x = np.ones(2) * 0.5
+ u = np.stack((np.ones((1, 1)), np.ones((1, 1))*0.5), axis=0)
+
+ linear_model = LinearModel(A, B)
+
+ pred_xs_alltogether = linear_model.predict_traj(curr_x, u)
+
+ expected_val = np.array([[[0.5, 0.5], [0.75, 1.3]],
+ [[0.5, 0.5], [0.65, 1.05]]])
+
+ assert pred_xs_alltogether == pytest.approx(expected_val)
\ No newline at end of file