add nmpc newton
This commit is contained in:
parent
2f5592f4e6
commit
17250480d7
|
|
@ -0,0 +1,79 @@
|
|||
# CGMRES method of Nonlinear Model Predictive Control
|
||||
This program is about Continuous gmres method for NMPC
|
||||
Although usually we have to calculate the partial differential of optimal matrix, it could be really complicated.
|
||||
By using CGMRES, we can pass the calculating step and get the optimal input quickly.
|
||||
|
||||
# Problem Formulation
|
||||
|
||||
- **example**
|
||||
|
||||
- model
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=\begin{bmatrix}&space;\dot{x_1}&space;\\&space;\dot{x_2}&space;\\&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;x_2&space;\\&space;(1-x_1^2-x_2^2)x_2-x_1+u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\begin{bmatrix}&space;\dot{x_1}&space;\\&space;\dot{x_2}&space;\\&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;x_2&space;\\&space;(1-x_1^2-x_2^2)x_2-x_1+u&space;\\&space;\end{bmatrix},&space;|u|&space;\leq&space;0.5" title="\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \\ \end{bmatrix} = \begin{bmatrix} x_2 \\ (1-x_1^2-x_2^2)x_2-x_1+u \\ \end{bmatrix}, |u| \leq 0.5" /></a>
|
||||
|
||||
- evaluation function
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" title="J = \frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau" /></a>
|
||||
|
||||
|
||||
- **two wheeled model**
|
||||
|
||||
- model
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\frac{d}{dt}&space;\boldsymbol{X}=&space;\frac{d}{dt}&space;\begin{bmatrix}&space;x&space;\\&space;y&space;\\&space;\theta&space;\end{bmatrix}&space;=&space;\begin{bmatrix}&space;\cos(\theta)&space;&&space;0&space;\\&space;\sin(\theta)&space;&&space;0&space;\\&space;0&space;&&space;1&space;\\&space;\end{bmatrix}&space;\begin{bmatrix}&space;u_v&space;\\&space;u_\omega&space;\\&space;\end{bmatrix}&space;=&space;\boldsymbol{B}\boldsymbol{U}" title="\frac{d}{dt} \boldsymbol{X}= \frac{d}{dt} \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} u_v \\ u_\omega \\ \end{bmatrix} = \boldsymbol{B}\boldsymbol{U}" /></a>
|
||||
|
||||
- evaluation function
|
||||
|
||||
<a href="https://www.codecogs.com/eqnedit.php?latex=J&space;=&space;\boldsymbol{X}(t_0+T)^2&space;+&space;\int_{t_0}^{t_0&space;+&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" target="_blank"><img src="https://latex.codecogs.com/gif.latex?J&space;=&space;\boldsymbol{X}(t_0+T)^2&space;+&space;\int_{t_0}^{t_0&space;+&space;T}&space;\boldsymbol{U}(t)^2&space;-&space;0.01&space;dummy_{u_v}&space;-&space;dummy_{u_\omega}&space;dt" title="J = \boldsymbol{X}(t_0+T)^2 + \int_{t_0}^{t_0 + T} \boldsymbol{U}(t)^2 - 0.01 dummy_{u_v} - dummy_{u_\omega} dt" /></a>
|
||||
|
||||
|
||||
if you want to see more detail about this methods, you should go https://qiita.com/MENDY/items/4108190a579395053924.
|
||||
However, it is written in Japanese
|
||||
|
||||
# Expected Results
|
||||
|
||||
- example
|
||||
|
||||

|
||||
|
||||
- two wheeled model
|
||||
|
||||
- trajectory
|
||||
|
||||
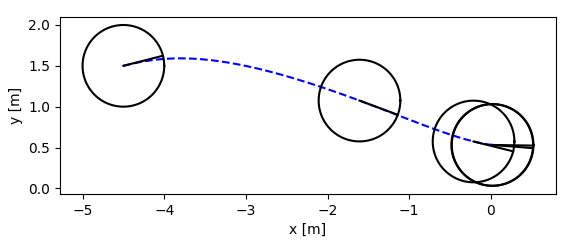
|
||||
|
||||
- time history
|
||||
|
||||

|
||||

|
||||
|
||||
# Usage
|
||||
|
||||
- for example
|
||||
|
||||
```
|
||||
$ python main_example.py
|
||||
```
|
||||
|
||||
- for two wheeled
|
||||
|
||||
```
|
||||
$ python main_two_wheeled.py
|
||||
```
|
||||
|
||||
# Requirement
|
||||
|
||||
- python3.5 or more
|
||||
- numpy
|
||||
- matplotlib
|
||||
|
||||
# Reference
|
||||
I`m sorry that main references are written in Japanese
|
||||
|
||||
- main (commentary article) (Japanse) https://qiita.com/MENDY/items/4108190a579395053924
|
||||
|
||||
- Ohtsuka, T., & Fujii, H. A. (1997). Real-time Optimization Algorithm for Nonlinear Receding-horizon Control. Automatica, 33(6), 1147–1154. https://doi.org/10.1016/S0005-1098(97)00005-8
|
||||
|
||||
- 非線形最適制御入門(コロナ社)
|
||||
|
||||
- 実時間最適化による制御の実応用(コロナ社)
|
||||
|
|
@ -0,0 +1,647 @@
|
|||
import numpy as np
|
||||
import matplotlib.pyplot as plt
|
||||
import math
|
||||
|
||||
class SampleSystem():
|
||||
"""SampleSystem, this is the simulator
|
||||
Attributes
|
||||
-----------
|
||||
x_1 : float
|
||||
system state 1
|
||||
x_2 : float
|
||||
system state 2
|
||||
history_x_1 : list
|
||||
time history of system state 1 (x_1)
|
||||
history_x_2 : list
|
||||
time history of system state 2 (x_2)
|
||||
"""
|
||||
def __init__(self, init_x_1=0., init_x_2=0.):
|
||||
"""
|
||||
Palameters
|
||||
-----------
|
||||
init_x_1 : float, optional
|
||||
initial value of x_1, default is 0.
|
||||
init_x_2 : float, optional
|
||||
initial value of x_2, default is 0.
|
||||
"""
|
||||
self.x_1 = init_x_1
|
||||
self.x_2 = init_x_2
|
||||
self.history_x_1 = [init_x_1]
|
||||
self.history_x_2 = [init_x_2]
|
||||
|
||||
def update_state(self, u, dt=0.01):
|
||||
"""
|
||||
Palameters
|
||||
------------
|
||||
u : float
|
||||
input of system in some cases this means the reference
|
||||
dt : float in seconds, optional
|
||||
sampling time of simulation, default is 0.01 [s]
|
||||
"""
|
||||
# for theta 1, theta 1 dot, theta 2, theta 2 dot
|
||||
k0 = [0.0 for _ in range(2)]
|
||||
k1 = [0.0 for _ in range(2)]
|
||||
k2 = [0.0 for _ in range(2)]
|
||||
k3 = [0.0 for _ in range(2)]
|
||||
|
||||
functions = [self._func_x_1, self._func_x_2]
|
||||
|
||||
# solve Runge-Kutta
|
||||
for i, func in enumerate(functions):
|
||||
k0[i] = dt * func(self.x_1, self.x_2, u)
|
||||
|
||||
for i, func in enumerate(functions):
|
||||
k1[i] = dt * func(self.x_1 + k0[0]/2., self.x_2 + k0[1]/2., u)
|
||||
|
||||
for i, func in enumerate(functions):
|
||||
k2[i] = dt * func(self.x_1 + k1[0]/2., self.x_2 + k1[1]/2., u)
|
||||
|
||||
for i, func in enumerate(functions):
|
||||
k3[i] = dt * func(self.x_1 + k2[0], self.x_2 + k2[1], u)
|
||||
|
||||
self.x_1 += (k0[0] + 2. * k1[0] + 2. * k2[0] + k3[0]) / 6.
|
||||
self.x_2 += (k0[1] + 2. * k1[1] + 2. * k2[1] + k3[1]) / 6.
|
||||
|
||||
# save
|
||||
self.history_x_1.append(self.x_1)
|
||||
self.history_x_2.append(self.x_2)
|
||||
|
||||
def _func_x_1(self, y_1, y_2, u):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
y_2 : float
|
||||
u : float
|
||||
system input
|
||||
"""
|
||||
y_dot = y_2
|
||||
return y_dot
|
||||
|
||||
def _func_x_2(self, y_1, y_2, u):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
y_2 : float
|
||||
u : float
|
||||
system input
|
||||
"""
|
||||
y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
|
||||
return y_dot
|
||||
|
||||
|
||||
class NMPCSimulatorSystem():
|
||||
"""SimulatorSystem for nmpc, this is the simulator of nmpc
|
||||
the reason why I seperate the real simulator and nmpc's simulator is sometimes the modeling error, disturbance can include in real simulator
|
||||
Attributes
|
||||
-----------
|
||||
|
||||
"""
|
||||
def __init__(self):
|
||||
"""
|
||||
Parameters
|
||||
-----------
|
||||
None
|
||||
"""
|
||||
pass
|
||||
|
||||
def calc_predict_and_adjoint_state(self, x_1, x_2, us, N, dt):
|
||||
"""main
|
||||
Parameters
|
||||
------------
|
||||
x_1 : float
|
||||
current state
|
||||
x_2 : float
|
||||
current state
|
||||
us : list of float
|
||||
estimated optimal input Us for N steps
|
||||
N : int
|
||||
predict step
|
||||
dt : float
|
||||
sampling time
|
||||
|
||||
Returns
|
||||
--------
|
||||
x_1s : list of float
|
||||
predicted x_1s for N steps
|
||||
x_2s : list of float
|
||||
predicted x_2s for N steps
|
||||
lam_1s : list of float
|
||||
adjoint state of x_1s, lam_1s for N steps
|
||||
lam_2s : list of float
|
||||
adjoint state of x_2s, lam_2s for N steps
|
||||
"""
|
||||
|
||||
x_1s, x_2s = self._calc_predict_states(x_1, x_2, us, N, dt) # by usin state equation
|
||||
lam_1s, lam_2s = self._calc_adjoint_states(x_1s, x_2s, us, N, dt) # by using adjoint equation
|
||||
|
||||
return x_1s, x_2s, lam_1s, lam_2s
|
||||
|
||||
def _calc_predict_states(self, x_1, x_2, us, N, dt):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
x_1 : float
|
||||
current state
|
||||
x_2 : float
|
||||
current state
|
||||
us : list of float
|
||||
estimated optimal input Us for N steps
|
||||
N : int
|
||||
predict step
|
||||
dt : float
|
||||
sampling time
|
||||
|
||||
Returns
|
||||
--------
|
||||
x_1s : list of float
|
||||
predicted x_1s for N steps
|
||||
x_2s : list of float
|
||||
predicted x_2s for N steps
|
||||
"""
|
||||
# initial state
|
||||
x_1s = [x_1]
|
||||
x_2s = [x_2]
|
||||
|
||||
for i in range(N):
|
||||
temp_x_1, temp_x_2 = self._predict_state_with_oylar(x_1s[i], x_2s[i], us[i], dt)
|
||||
x_1s.append(temp_x_1)
|
||||
x_2s.append(temp_x_2)
|
||||
|
||||
return x_1s, x_2s
|
||||
|
||||
def _calc_adjoint_states(self, x_1s, x_2s, us, N, dt):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
x_1s : list of float
|
||||
predicted x_1s for N steps
|
||||
x_2s : list of float
|
||||
predicted x_2s for N steps
|
||||
us : list of float
|
||||
estimated optimal input Us for N steps
|
||||
N : int
|
||||
predict step
|
||||
dt : float
|
||||
sampling time
|
||||
|
||||
Returns
|
||||
--------
|
||||
lam_1s : list of float
|
||||
adjoint state of x_1s, lam_1s for N steps
|
||||
lam_2s : list of float
|
||||
adjoint state of x_2s, lam_2s for N steps
|
||||
"""
|
||||
# final state
|
||||
# final_state_func
|
||||
lam_1s = [x_1s[-1]]
|
||||
lam_2s = [x_2s[-1]]
|
||||
|
||||
for i in range(N-1, 0, -1):
|
||||
temp_lam_1, temp_lam_2 = self._adjoint_state_with_oylar(x_1s[i], x_2s[i], lam_1s[0] ,lam_2s[0], us[i], dt)
|
||||
lam_1s.insert(0, temp_lam_1)
|
||||
lam_2s.insert(0, temp_lam_2)
|
||||
|
||||
return lam_1s, lam_2s
|
||||
|
||||
def final_state_func(self):
|
||||
"""this func usually need
|
||||
"""
|
||||
pass
|
||||
|
||||
def _predict_state_with_oylar(self, x_1, x_2, u, dt):
|
||||
"""in this case this function is the same as simulator
|
||||
Parameters
|
||||
------------
|
||||
x_1 : float
|
||||
system state
|
||||
x_2 : float
|
||||
system state
|
||||
u : float
|
||||
system input
|
||||
dt : float in seconds
|
||||
sampling time
|
||||
Returns
|
||||
--------
|
||||
next_x_1 : float
|
||||
next state, x_1 calculated by using state equation
|
||||
next_x_2 : float
|
||||
next state, x_2 calculated by using state equation
|
||||
"""
|
||||
k0 = [0. for _ in range(2)]
|
||||
|
||||
functions = [self.func_x_1, self.func_x_2]
|
||||
|
||||
for i, func in enumerate(functions):
|
||||
k0[i] = dt * func(x_1, x_2, u)
|
||||
|
||||
next_x_1 = x_1 + k0[0]
|
||||
next_x_2 = x_2 + k0[1]
|
||||
|
||||
return next_x_1, next_x_2
|
||||
|
||||
def func_x_1(self, y_1, y_2, u):
|
||||
"""calculating \dot{x_1}
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
means x_1
|
||||
y_2 : float
|
||||
means x_2
|
||||
u : float
|
||||
means system input
|
||||
Returns
|
||||
---------
|
||||
y_dot : float
|
||||
means \dot{x_1}
|
||||
"""
|
||||
y_dot = y_2
|
||||
return y_dot
|
||||
|
||||
def func_x_2(self, y_1, y_2, u):
|
||||
"""calculating \dot{x_2}
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
means x_1
|
||||
y_2 : float
|
||||
means x_2
|
||||
u : float
|
||||
means system input
|
||||
Returns
|
||||
---------
|
||||
y_dot : float
|
||||
means \dot{x_2}
|
||||
"""
|
||||
y_dot = (1. - y_1**2 - y_2**2) * y_2 - y_1 + u
|
||||
return y_dot
|
||||
|
||||
def _adjoint_state_with_oylar(self, x_1, x_2, lam_1, lam_2, u, dt):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
x_1 : float
|
||||
system state
|
||||
x_2 : float
|
||||
system state
|
||||
lam_1 : float
|
||||
adjoint state
|
||||
lam_2 : float
|
||||
adjoint state
|
||||
u : float
|
||||
system input
|
||||
dt : float in seconds
|
||||
sampling time
|
||||
Returns
|
||||
--------
|
||||
pre_lam_1 : float
|
||||
pre, 1 step before lam_1 calculated by using adjoint equation
|
||||
pre_lam_2 : float
|
||||
pre, 1 step before lam_2 calculated by using adjoint equation
|
||||
"""
|
||||
k0 = [0. for _ in range(2)]
|
||||
|
||||
functions = [self._func_lam_1, self._func_lam_2]
|
||||
|
||||
for i, func in enumerate(functions):
|
||||
k0[i] = dt * func(x_1, x_2, lam_1, lam_2, u)
|
||||
|
||||
pre_lam_1 = lam_1 + k0[0]
|
||||
pre_lam_2 = lam_2 + k0[1]
|
||||
|
||||
return pre_lam_1, pre_lam_2
|
||||
|
||||
def _func_lam_1(self, y_1, y_2, y_3, y_4, u):
|
||||
"""calculating -\dot{lam_1}
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
means x_1
|
||||
y_2 : float
|
||||
means x_2
|
||||
y_3 : float
|
||||
means lam_1
|
||||
y_4 : float
|
||||
means lam_2
|
||||
u : float
|
||||
means system input
|
||||
Returns
|
||||
---------
|
||||
y_dot : float
|
||||
means -\dot{lam_1}
|
||||
"""
|
||||
y_dot = y_1 - (2. * y_1 * y_2 + 1.) * y_4
|
||||
return y_dot
|
||||
|
||||
def _func_lam_2(self, y_1, y_2, y_3, y_4, u):
|
||||
"""calculating -\dot{lam_2}
|
||||
Parameters
|
||||
------------
|
||||
y_1 : float
|
||||
means x_1
|
||||
y_2 : float
|
||||
means x_2
|
||||
y_3 : float
|
||||
means lam_1
|
||||
y_4 : float
|
||||
means lam_2
|
||||
u : float
|
||||
means system input
|
||||
Returns
|
||||
---------
|
||||
y_dot : float
|
||||
means -\dot{lam_2}
|
||||
"""
|
||||
y_dot = y_2 + y_3 + (-3. * (y_2**2) - y_1**2 + 1. ) * y_4
|
||||
return y_dot
|
||||
|
||||
|
||||
def calc_numerical_gradient(f, x, shape):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
f : function
|
||||
forward function of NN
|
||||
x : numpy.ndarray
|
||||
input
|
||||
shape : tuple
|
||||
jacobian shape
|
||||
|
||||
Returns
|
||||
---------
|
||||
grad : numpy.ndarray, shape is the same as shape
|
||||
results of numercial gradient of the input
|
||||
References
|
||||
-----------
|
||||
- oreilly japan 0 から作るdeeplearning
|
||||
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/gradient.py
|
||||
"""
|
||||
# check condition
|
||||
if not callable(f):
|
||||
raise TypeError("f should be callable")
|
||||
|
||||
if not (isinstance(x, list) or isinstance(x, np.ndarray)):
|
||||
raise TypeError("x should be array-like")
|
||||
|
||||
h = 1e-3 # 0.01
|
||||
grad = np.zeros(shape)
|
||||
|
||||
for idx in range(x.size):
|
||||
# save
|
||||
tmp_val = x[idx]
|
||||
|
||||
x[idx] = float(tmp_val) + h
|
||||
fxh1 = f(x) # f(x+h)
|
||||
|
||||
x[idx] = float(tmp_val) - h
|
||||
fxh2 = f(x) # f(x-h)
|
||||
|
||||
grad[:, idx] = (fxh1 - fxh2) / (2*h)
|
||||
|
||||
x[idx] = tmp_val
|
||||
|
||||
return np.array(grad)
|
||||
|
||||
class NMPCControllerWithNewton():
|
||||
"""
|
||||
Attributes
|
||||
------------
|
||||
zeta : float
|
||||
gain of optimal answer stability
|
||||
tf : float
|
||||
predict time
|
||||
alpha : float
|
||||
gain of predict time
|
||||
N : int
|
||||
predicte step, discritize value
|
||||
threshold : float
|
||||
cgmres's threshold value
|
||||
input_num : int
|
||||
system input length, this should include dummy u and constraint variables
|
||||
max_iteration : int
|
||||
decide by the solved matrix size
|
||||
simulator : NMPCSimulatorSystem class
|
||||
us : list of float
|
||||
estimated optimal system input
|
||||
dummy_us : list of float
|
||||
estimated dummy input
|
||||
raws : list of float
|
||||
estimated constraint variable
|
||||
history_u : list of float
|
||||
time history of actual system input
|
||||
history_dummy_u : list of float
|
||||
time history of actual dummy u
|
||||
history_raw : list of float
|
||||
time history of actual raw
|
||||
history_f : list of float
|
||||
time history of error of optimal
|
||||
"""
|
||||
def __init__(self):
|
||||
"""
|
||||
Parameters
|
||||
-----------
|
||||
None
|
||||
"""
|
||||
# parameters
|
||||
self.tf = 1. # 最終時間
|
||||
self.N = 10 # 分割数
|
||||
self.threshold = 0.0001 # break値
|
||||
|
||||
self.NUM_INPUT = 3 # dummy, 制約条件に対するrawにも合わせた入力の数
|
||||
self.Jacobian_size = self.NUM_INPUT * self.N
|
||||
|
||||
# newton parameters
|
||||
self.MAX_ITERATION = 100
|
||||
|
||||
# simulator
|
||||
self.simulator = NMPCSimulatorSystem()
|
||||
|
||||
# initial
|
||||
self.us = np.zeros(self.N)
|
||||
self.dummy_us = np.ones(self.N) * 0.25
|
||||
self.raws = np.ones(self.N) * 0.01
|
||||
|
||||
# for fig
|
||||
self.history_u = []
|
||||
self.history_dummy_u = []
|
||||
self.history_raw = []
|
||||
self.history_f = []
|
||||
|
||||
def calc_input(self, x_1, x_2, time):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
x_1 : float
|
||||
current state
|
||||
x_2 : float
|
||||
current state
|
||||
time : float in seconds
|
||||
now time
|
||||
Returns
|
||||
--------
|
||||
us : list of float
|
||||
estimated optimal system input
|
||||
"""
|
||||
# calculating sampling time
|
||||
dt = 0.01
|
||||
|
||||
# concat all us, shape (NUM_INPUT, N)
|
||||
all_us = np.stack((self.us, self.dummy_us, self.raws))
|
||||
all_us = all_us.T.flatten()
|
||||
|
||||
# Newton method
|
||||
for i in range(self.MAX_ITERATION):
|
||||
# check
|
||||
# print("all_us = {}".format(all_us))
|
||||
# print("newton iteration in {}".format(i))
|
||||
# input()
|
||||
|
||||
# calc all state
|
||||
x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
|
||||
|
||||
# F
|
||||
F_hat = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
|
||||
|
||||
# judge
|
||||
# print("F_hat = {}".format(F_hat))
|
||||
# print(np.linalg.norm(F_hat))
|
||||
if np.linalg.norm(F_hat) < self.threshold:
|
||||
# print("break!!")
|
||||
break
|
||||
|
||||
grad_f = lambda all_us : self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
|
||||
grads = calc_numerical_gradient(grad_f, all_us, (self.Jacobian_size, self.Jacobian_size))
|
||||
|
||||
# make jacobian and calc inverse of it
|
||||
# all us
|
||||
all_us = all_us - np.dot(np.linalg.inv(grads), F_hat)
|
||||
|
||||
# update
|
||||
self.us = all_us[::self.NUM_INPUT]
|
||||
self.dummy_us = all_us[1::self.NUM_INPUT]
|
||||
self.raws = all_us[2::self.NUM_INPUT]
|
||||
|
||||
# final insert
|
||||
self.us = all_us[::self.NUM_INPUT]
|
||||
self.dummy_us = all_us[1::self.NUM_INPUT]
|
||||
self.raws = all_us[2::self.NUM_INPUT]
|
||||
|
||||
x_1s, x_2s, lam_1s, lam_2s = self.simulator.calc_predict_and_adjoint_state(x_1, x_2, self.us, self.N, dt)
|
||||
|
||||
F = self._calc_f(x_1s, x_2s, lam_1s, lam_2s, all_us, self.N, dt)
|
||||
|
||||
# print("check val of F = {0}".format(np.linalg.norm(F)))
|
||||
# input()
|
||||
|
||||
# for save
|
||||
self.history_f.append(np.linalg.norm(F))
|
||||
self.history_u.append(self.us[0])
|
||||
self.history_dummy_u.append(self.dummy_us[0])
|
||||
self.history_raw.append(self.raws[0])
|
||||
|
||||
return self.us
|
||||
|
||||
def _calc_f(self, x_1s, x_2s, lam_1s, lam_2s, all_us, N, dt):
|
||||
"""
|
||||
Parameters
|
||||
------------
|
||||
x_1s : list of float
|
||||
predicted x_1s for N steps
|
||||
x_2s : list of float
|
||||
predicted x_2s for N steps
|
||||
lam_1s : list of float
|
||||
adjoint state of x_1s, lam_1s for N steps
|
||||
lam_2s : list of float
|
||||
adjoint state of x_2s, lam_2s for N steps
|
||||
us : list of float
|
||||
estimated optimal system input
|
||||
dummy_us : list of float
|
||||
estimated dummy input
|
||||
raws : list of float
|
||||
estimated constraint variable
|
||||
N : int
|
||||
predict time step
|
||||
dt : float
|
||||
sampling time of system
|
||||
"""
|
||||
F = []
|
||||
|
||||
us = all_us[::self.NUM_INPUT]
|
||||
dummy_us = all_us[1::self.NUM_INPUT]
|
||||
raws = all_us[2::self.NUM_INPUT]
|
||||
|
||||
for i in range(N):
|
||||
F.append(0.5 * us[i] + lam_2s[i] + 2. * raws[i] * us[i])
|
||||
F.append(-0.01 + 2. * raws[i] * dummy_us[i])
|
||||
F.append(us[i]**2 + dummy_us[i]**2 - 0.5**2)
|
||||
|
||||
return np.array(F)
|
||||
|
||||
def main():
|
||||
# simulation time
|
||||
dt = 0.01
|
||||
iteration_time = 20.
|
||||
iteration_num = int(iteration_time/dt)
|
||||
|
||||
# plant
|
||||
plant_system = SampleSystem(init_x_1=2., init_x_2=0.)
|
||||
|
||||
# controller
|
||||
controller = NMPCControllerWithNewton()
|
||||
|
||||
# for i in range(iteration_num)
|
||||
for i in range(1, iteration_num):
|
||||
print("iteration = {}".format(i))
|
||||
time = float(i) * dt
|
||||
x_1 = plant_system.x_1
|
||||
x_2 = plant_system.x_2
|
||||
# make input
|
||||
us = controller.calc_input(x_1, x_2, time)
|
||||
# update state
|
||||
plant_system.update_state(us[0])
|
||||
|
||||
# figure
|
||||
fig = plt.figure()
|
||||
|
||||
x_1_fig = fig.add_subplot(321)
|
||||
x_2_fig = fig.add_subplot(322)
|
||||
u_fig = fig.add_subplot(323)
|
||||
dummy_fig = fig.add_subplot(324)
|
||||
raw_fig = fig.add_subplot(325)
|
||||
f_fig = fig.add_subplot(326)
|
||||
|
||||
x_1_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_1)
|
||||
x_1_fig.set_xlabel("time [s]")
|
||||
x_1_fig.set_ylabel("x_1")
|
||||
|
||||
x_2_fig.plot(np.arange(iteration_num)*dt, plant_system.history_x_2)
|
||||
x_2_fig.set_xlabel("time [s]")
|
||||
x_2_fig.set_ylabel("x_2")
|
||||
|
||||
u_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_u)
|
||||
u_fig.set_xlabel("time [s]")
|
||||
u_fig.set_ylabel("u")
|
||||
|
||||
dummy_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_dummy_u)
|
||||
dummy_fig.set_xlabel("time [s]")
|
||||
dummy_fig.set_ylabel("dummy u")
|
||||
|
||||
raw_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_raw)
|
||||
raw_fig.set_xlabel("time [s]")
|
||||
raw_fig.set_ylabel("raw")
|
||||
|
||||
f_fig.plot(np.arange(iteration_num - 1)*dt, controller.history_f)
|
||||
f_fig.set_xlabel("time [s]")
|
||||
f_fig.set_ylabel("optimal error")
|
||||
|
||||
fig.tight_layout()
|
||||
|
||||
plt.show()
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
|
||||
Loading…
Reference in New Issue